Презентация на тему Разложение многочлена на множители

приемов.
Три пути ведут к познанию:
путь размышления – это

путь самый благородный,
путь подражания – этот путь самый легкий
и путь опыта – этот путь самый горький.
Конфуций

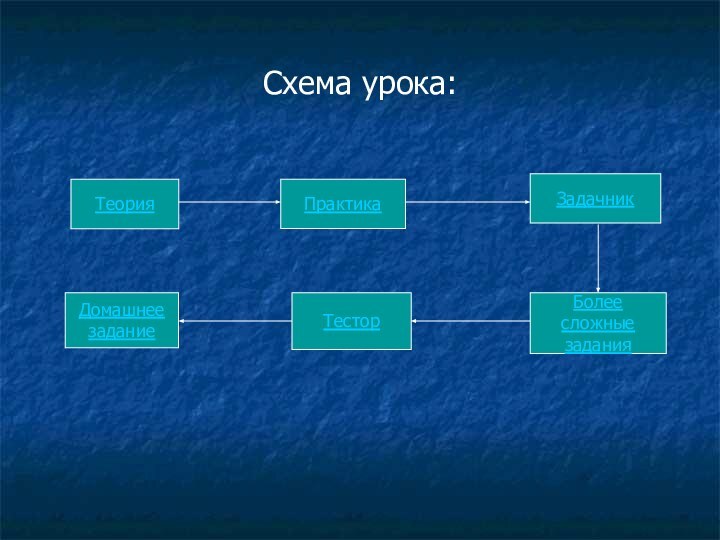
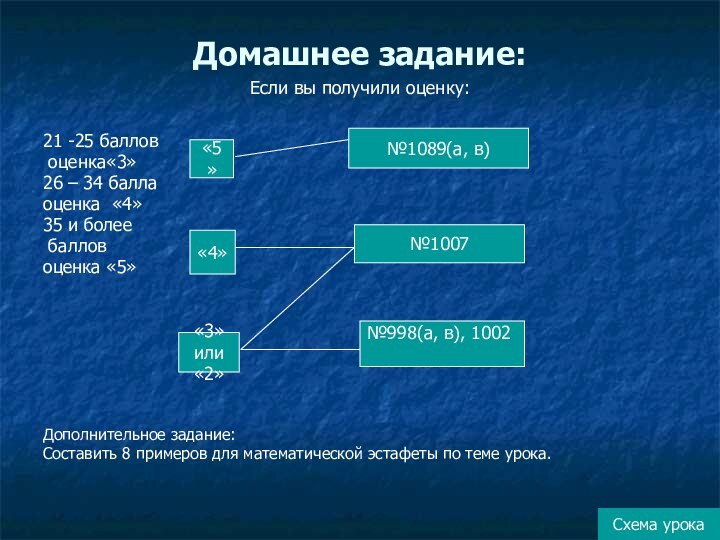
Схема урока:

Теория
Более
сложные
задания
Тестор
Задачник
Домашнее
задание
Практика

многочлена в виде произведения двух или нескольких многочленов

Комбинировали три приема:
Вынесение общего множителя за скобки
С помощью формул сокращенного умножения
Способ группировки

Схема урока

множители.

Метод разложения на множители
Формулы сокращенного
умножения
Способ группировки
20х3у2 +

4х2у 15а3b + 3а2b3
а4 –b8 а2 + аb – 5а - 5b
2bх – 3ау - 6bу + ах 2ап - 5bm - 10bп + аm
27b3 +а6 3а2 + 3аb – 7а - 7b
Х2 + 6х + 9 49m4 – 25п2
b(а +5) – с(а + 5) 2у(х – 5) + х(х – 5)

Вынесение общего
множителя за скобки

ответы

Схема урока

множители.






20х3у2 +4х2у

а4 – b8 2bх -3ау -6bу + ах
b(а +5) - с(а +5) 27b3 + а6 а2 + аb – 5а -5b
15а3b +3а2b3 х2 + 6х + 9 2аn -5bm -10bn + аm
2у(х – 5) +х(х – 5) 49m4 - 25n2 3а2 +3аb -7а -7b
За каждый, верно записанный многочлен, 1 балл.

Формулы сокращенного
умножения

Способ
группировки

Метод разложения на множители

Вынесение
общего множителя за
скобки

теория

в многочлен, выносится некоторый одночлен, входящий в качестве множителя

во все слагаемые.
Таким общим множителем может быть не только одночлен, но и многочлен.

теория

(или более) слагаемых, которая обращает выражение, входящее в одну

из формул сокращенного умножения, заменяется произведением многочленов.
а2 + 2аb + b2 = (а + b)2
а2 - 2аb + b2 = (а - b)2
а2 - b2 = (а – b)(а + b)
а3 + b3 = (а + b)(а2 - аb + b2)
а3 - b3 = (а - b)(а2 + аb + b2)

теория

общего множителя, но после заключения нескольких членов в скобки

(на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.
Чтобы разложить многочлен на множители способом группировки, нужно:
Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
Вынести в каждой группе общий множитель в виде одночлена за скобки
Вынести в каждой группе общий множитель (в виде многочлена) за скобки.

теория

+ 12b = 3(а + 4 b)
2у(х - 5)

+ х(х – 5) = (х – 5)(2у + х)
С помощью формул сокращенного умножения
Пример:
4х2 + 12ху + 9у2 = (2х + 3у)2
125а3 – 64х3 = (5а – 4х)(25а2 + 20ах + 16х2)
49х4у6 - 0,01а2 = (7х2у3 – 0,1а) (7х2у3 + 0,1а)
Способ группировки
Пример:
3а2 +3аb – 7а - 7b = (3а2 + 3аb) – (7а + 7b) = 3а(а + b) – 7(а + b) = (а + b)(3а – 7)

скобку (если он есть)
Попробовать разложить многочлен на множители по

формулам сокращенного умножения
Попытаться применить способ группировки
(если предыдущие способы не привели к цели)

Схема урока

урока

– 4)=
- 2b2 + 18= -2(b2 - 9)=
3а2 +

6а + 3= 3(а2 +2а +1)=
- х2 +4х - 4= - (х2 - 4х +4)=
с2 - b2 + 8с +8b =(с2 - b2) + (8с+8b)=(с – b)(с + b) +8(с + b)=
х2 – у2 – 3х – 3у=(х2 – у2) – (3х +3у)=
За каждое правильно выполненное задание один балл.

ответы

Задачник

+ 3)
3(а +1)2
- (х – 2)2
(с + b)(с –

b + 8)
(х – у)(х + у) – 3(х + у)=(х +у)(х – у – 3)

у4
4а2b – 8аb +4b
- 10х2 +40ах – 40а2
х2 –

2ху +у2 – 6х +6у
4а2 +4аb + b2 +12а +6b
За каждое правильно выполненное задание два балла.

ответы

Задачник

– 1)2
- 10(х – 2а)2
(х – у)(х – у

– 6)
(2а + b) (2а + b +6)

у3 +ху2 – у
а4 – а3b + а2b –

аb2
9х2 – 12х + 4 – у2
с2 – х2 – 2ху – у2
а6 – а4 + а2 - 1
За каждое правильно выполненное задание три балла.

Ответы

Задачник

b)
(3х - 2 – у)(3х – 2 +у)
(с –

х – у)(с + х + у)
(а2 – 1)(а4 + 1)

+2n + n +2)= n((n2 +2n) + (n +2))=
n(n(n

+2)+(n +2))=n(n +2)(n +1)
Для решения этого примера мы использовали еще один прием разложения на множители – предварительное преобразование

Схема урока

Задания

или дополняется путем прибавления к нему некоторого слагаемого. В

последнем случае, чтобы многочлен не изменился, от него отнимается такое же слагаемое.

+5)2 – 4=0
(х +5 -2)(х +5 + 2)=0
(х +3)(х

+7)=0
х +3 =0 или х +7 =0
х = -3 или х = -7
Ответ: -3; -7.
Метод выделения полного квадрата.

Сложный уровень

тождество:
(а2 +3а)2 +2(а2 +3а)= а(а+1)(а+2)(а+3)
3.Разложите на множители:
а)х2 – 3х

+2
bb)х2 + 4х +3
За каждое правильно выполненное задание 4 балла.

Сложный уровень

– 8х +56 =0
(х2 – 7х) – (8х –

56) = 0
х(х – 7) – 8(х – 7) =0
(х – 7)(х – 8) =0
х -7 =0 или х – 8 =0
х=7 или х=8
Ответ: 7;8

Сложные задания

а(а + 1) (а + 2)(а + 3)
(а2 +

3а)2 +2(а2 + 3а) = (а2 + 3а)(а2 + 3а) +
2(а2 +3а) = (а2 + 3а)(а2 + 3а + 2) =
(а(а + 3))(а2 + 2а + а + 1 +1) =
а(а + 3)((а2 + 2а + 1) +(а + 1)) =
а(а +3)((а + 1)2 +(а + 1)) =
а(а +3)(а + 1)(а + 1 + 1) =
а(а + 3)(а + 1)(а + 2) = а(а + 1)(а + 2)(а + 3)

Сложные задания

= х2 – 2х – х + 1 +

1 =
(х2 – 2х + 1) – (х – 1) = (х – 1)2 – (х – 1) =
(х – 1)(х – 1 – 1) = (х – 1)(х – 2)

Сложные задания

= х2 + 4х + 4 – 1 =

(х2 + 4х + 4) – 1 =(х + 2)2 – 12 =
(х + 2 – 1)(х + 2 + 1) = (х + 1)(х + 3)

Сложные задания

125аb2
5а(а - 55а(а - 5b5а(а - 5b)(а + 55а(а

- 5b)(а + 5b5а(а - 5b)(а + 5b) 5а(а2 - 25 - 25 b2) 5а(а - 55а(а - 5b5а(а - 5b)2
63аb3 – 7а2b
7а2b2(9(9b(9b – 1) а(9b – 1) аb(9b – 1) аb(63 (9b – 1) аb(63 b2 – 7а) – 7а) 7а – 7а) 7аb – 7а) 7аb(9 – 7а) 7аb(9b2 – а)
3а2 + 6а + 3
3(а +1)(а – 1) 3(а +1)(а – 1) 3(а + 1)2 (3а + 1)2
а2 - b2 + 6а +6b
(а + (а + b(а + b)(а – (а + b)(а – b(а + b)(а – b + 6) (а + b)(а – b + 6) ( а – (а + b)(а – b + 6) ( а – b(а + b)(а – b + 6) ( а – b)2 (а2 - - b2) + (6а + 6) + (6а + 6b) + (6а + 6b)
6х2 – 12х + 6
(3х – 3)2 6(х – 1)2 (х – 1)(х + 6)

Схема урока