Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Решение простейших тригонометрических неравенств

Содержание

Под простейшими тригонометрическими неравенствами понимают неравенства вида:,где t – выражение с переменной, a∈.Под знаком “” следует понимать любой из четырёх знаков неравенств: , , .
Воробьев Леонид Альбертович, г.МинскАлгебра и начала анализа, 10 класс.Решение простейших тригонометрических неравенств. Под простейшими тригонометрическими неравенствами понимают неравенства вида:,где t – выражение с переменной, Для решения тригонометрических неравенств необходимо уметь работать с тригонометрическим кругом:sintcost txy0101sint - xy0101–1–1a  1a  –1Аналогично, неравенство sinta, при a 1 не имеет xy0101–1–1a  1a  –1Если знак неравенства нестрогий, то неравенство sint  xy0101t=arcsinat=π–arcsinaa–1–12πADBCВыбор скобок в записи ответа зависит от знака неравенстваДугу ∪CBA можно записать 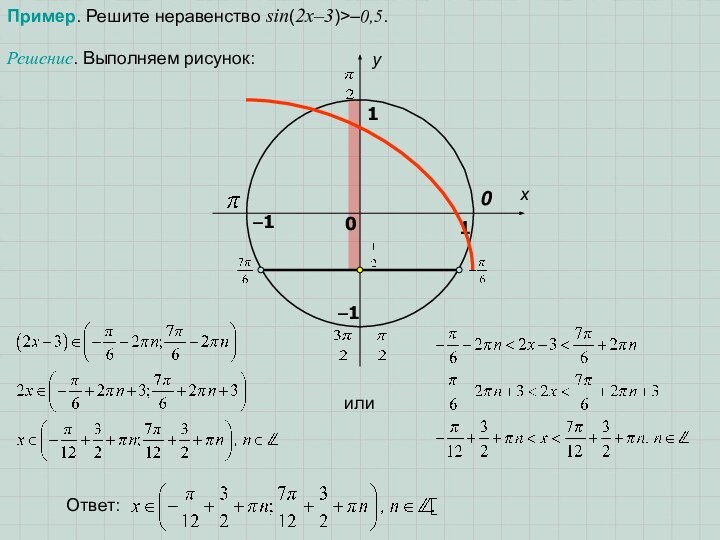Пример. Решите неравенство sin(2x–3)>–0,5.Решение. 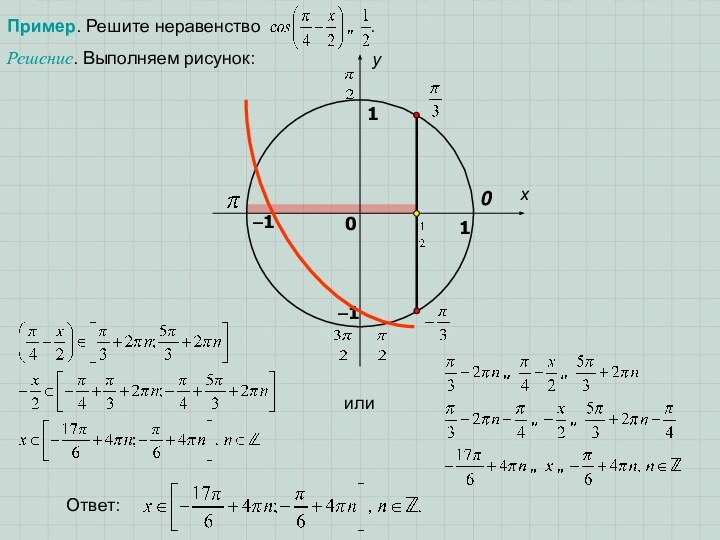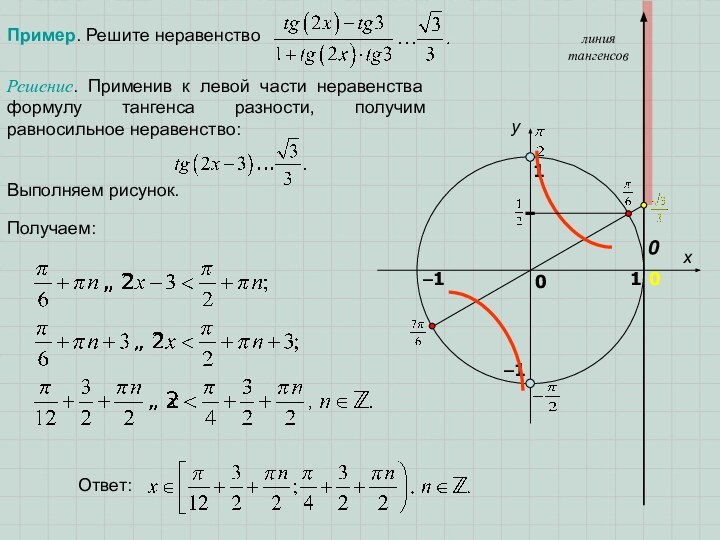Выполняем рисунок:или xy0101–1–1a  –1a  1Для неравенство cost>a, при a 1 и cost xy0101–1–1a  1a  –1Если знак неравенства нестрогий, то неравенство cost  xy011–1–12πADBCВыбор скобок в записи ответа зависит от знака неравенства0t=arccosat=–arccosaa Пример. Решите неравенство .Решение. Выполняем рисунок:или xy101–10линия тангенсовaТак как E(tg)=, то неравенство tgta всегда имеет решение.–1Значению tgt=a соответствуют xy101–10линия котангенсовa–1Проследите за ходом решения и выведите общие формулы для неравенств:Так как Пример. Решите неравенство xy101–10линия тангенсов–10Решение. Применив к левой части неравенства формулу тангенса
Слайды презентации

Слайд 2 Под простейшими тригонометрическими неравенствами понимают неравенства вида:
,где t

Под простейшими тригонометрическими неравенствами понимают неравенства вида:,где t – выражение с

– выражение с переменной, a∈.

Под знаком “” следует понимать

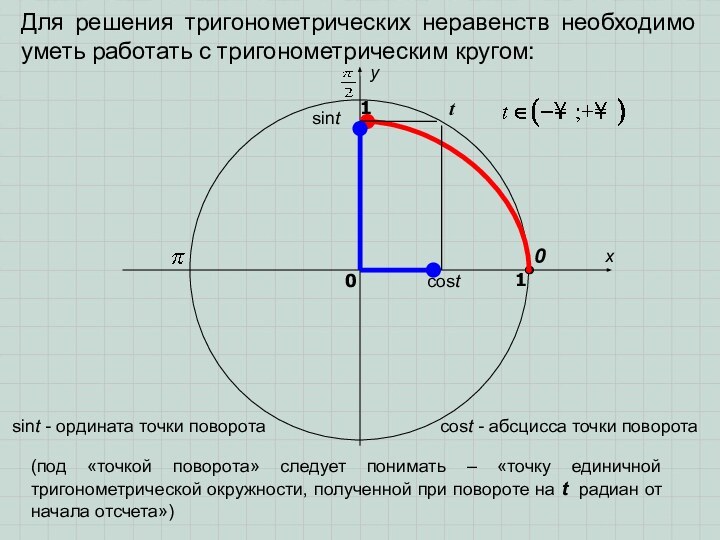
любой из четырёх знаков неравенств: <, >, , .

Слайд 3 Для решения тригонометрических неравенств необходимо уметь работать с

Для решения тригонометрических неравенств необходимо уметь работать с тригонометрическим кругом:sintcost txy0101sint

тригонометрическим кругом:



sint
cost
t
x
y
0
1
0

1
sint - ордината точки поворота
cost - абсцисса

точки поворота

(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)

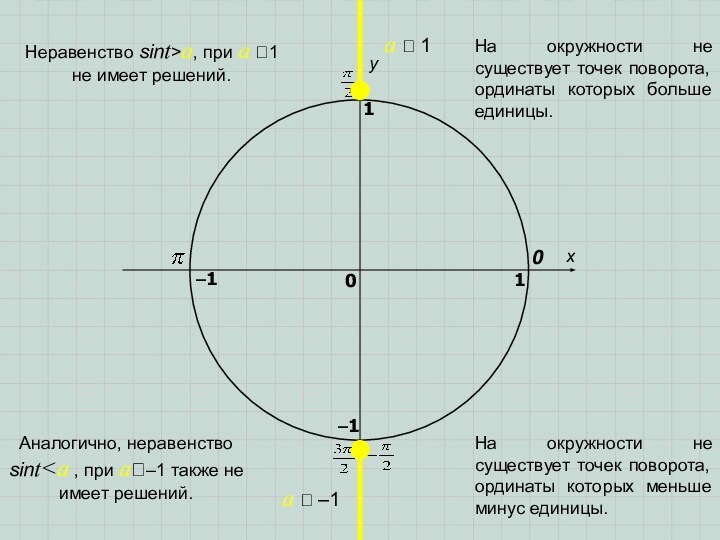
Слайд 4
x
y
0
1
0
1
–1
–1
a  1
a  –1
Аналогично, неравенство sint

xy0101–1–1a  1a  –1Аналогично, неравенство sinta, при a 1 не

при a–1 также не имеет решений.
Неравенство sint>a, при a

1 не имеет решений.

На окружности не существует точек поворота, ординаты которых больше единицы.

На окружности не существует точек поворота, ординаты которых меньше минус единицы.

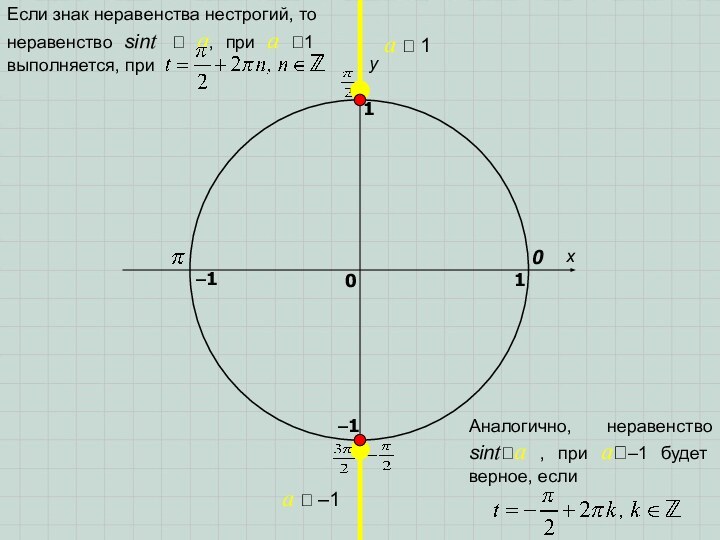
Слайд 5
x
y
0
1
0
1
–1
–1
a  1
a  –1
Если знак неравенства нестрогий,

xy0101–1–1a  1a  –1Если знак неравенства нестрогий, то неравенство sint

то неравенство sint  a, при a 1 выполняется,

при


Аналогично, неравенство sinta , при a–1 будет верное, если


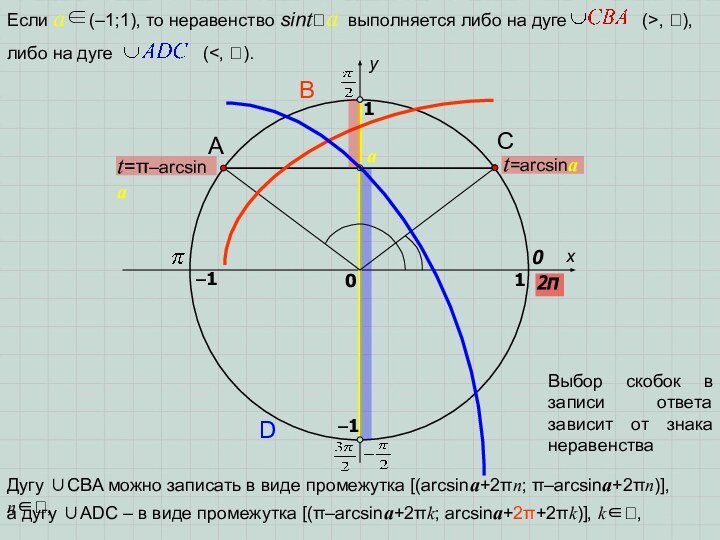
Слайд 6



x
y
0
1
0

1
t=arcsina
t=π–arcsina
a
–1
–1





2π


A
D
B
C
Выбор скобок в записи ответа зависит от знака

xy0101t=arcsinat=π–arcsinaa–1–12πADBCВыбор скобок в записи ответа зависит от знака неравенстваДугу ∪CBA можно

неравенства


Дугу ∪CBA можно записать в виде промежутка [(arcsina+2πn; π–arcsina+2πn)],

n∈,


а дугу ∪ADC – в виде промежутка [(π–arcsina+2πk; arcsina+2π+2πk)], k∈,

Слайд 7
Пример. Решите неравенство sin(2x–3)>–0,5.
Решение. Выполняем рисунок:

или


Пример. Решите неравенство sin(2x–3)>–0,5.Решение. Выполняем рисунок:или

Слайд 8
x
y
0
1
0

1
–1
–1
a  –1
a  1
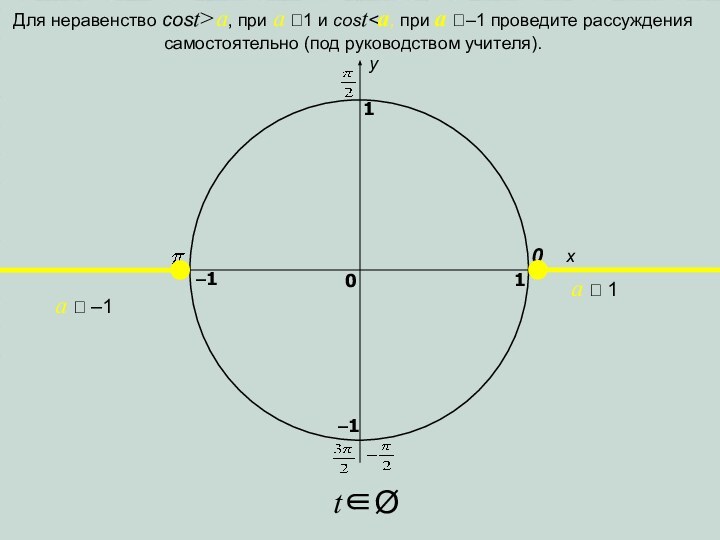
Для неравенство cost>a, при

xy0101–1–1a  –1a  1Для неравенство cost>a, при a 1 и cost

a 1 и cost

самостоятельно (под руководством учителя).

t∈Ø

Слайд 9
x
y
0
1
0
1
–1
–1
a  1
a  –1
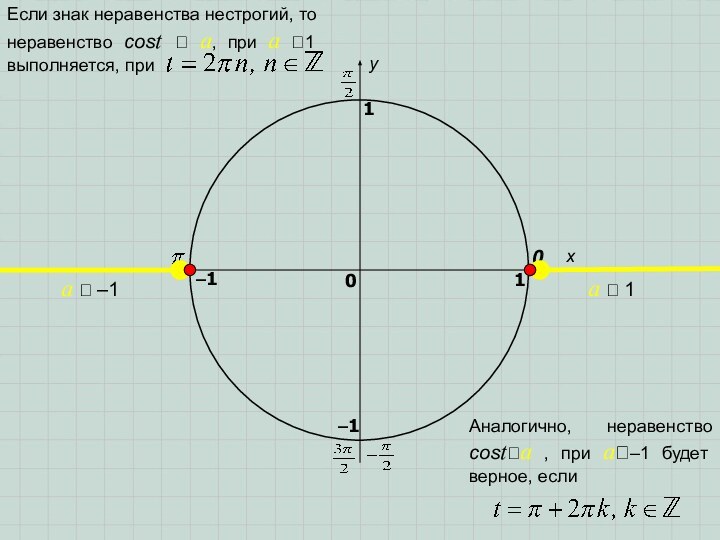
Если знак неравенства нестрогий,

xy0101–1–1a  1a  –1Если знак неравенства нестрогий, то неравенство cost

то неравенство cost  a, при a 1 выполняется,

при


Аналогично, неравенство costa , при a–1 будет верное, если


Слайд 10


x
y
0
1
1
–1
–1
2π


A
D
B
C
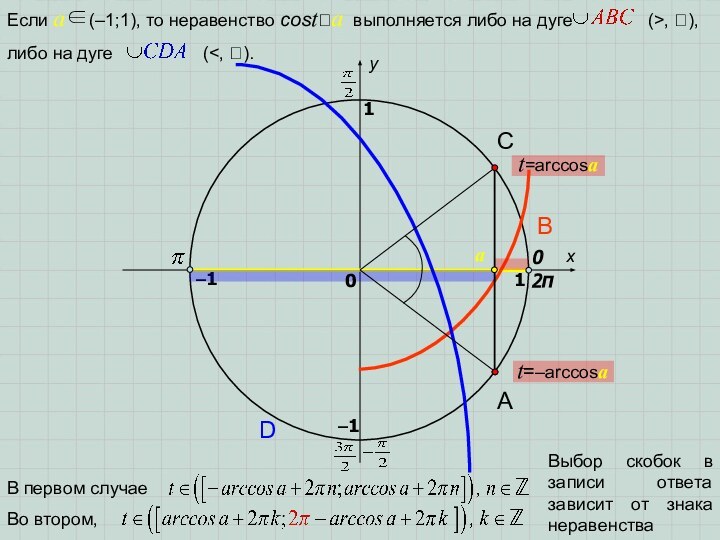
Выбор скобок в записи ответа зависит от знака

xy011–1–12πADBCВыбор скобок в записи ответа зависит от знака неравенства0t=arccosat=–arccosaa

неравенства



0
t=arccosa
t=–arccosa
a





Слайд 11
Пример. Решите неравенство

Пример. Решите неравенство .Решение. Выполняем рисунок:или

.
Решение. Выполняем рисунок:



или

Слайд 12 x
y
1
0
1
–1

0
линия тангенсов



a


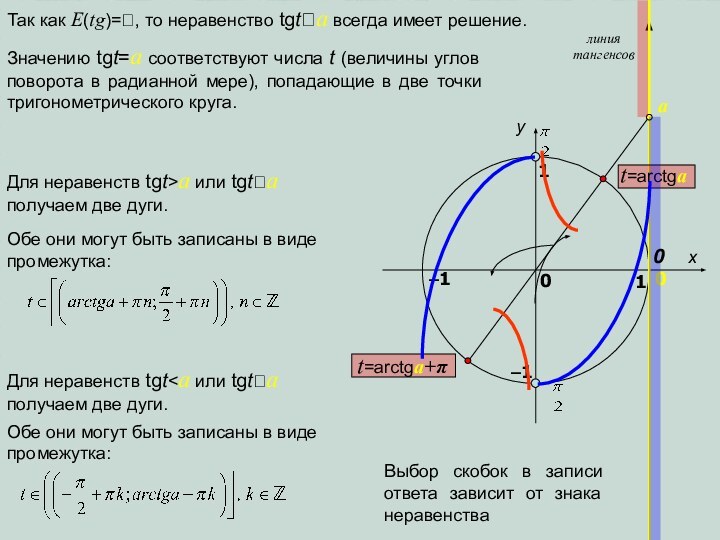
Так как E(tg)=, то неравенство tgta всегда

xy101–10линия тангенсовaТак как E(tg)=, то неравенство tgta всегда имеет решение.–1Значению tgt=a

имеет решение.
–1
Значению tgt=a соответствуют числа t (величины углов поворота

в радианной мере), попадающие в две точки тригонометрического круга.

Для неравенств tgt>a или tgta получаем две дуги.


Обе они могут быть записаны в виде промежутка:

Для неравенств tgt


0

Обе они могут быть записаны в виде промежутка:

Выбор скобок в записи ответа зависит от знака неравенства

Слайд 13 x
y
1
0
1
–1

0
линия котангенсов



a


–1
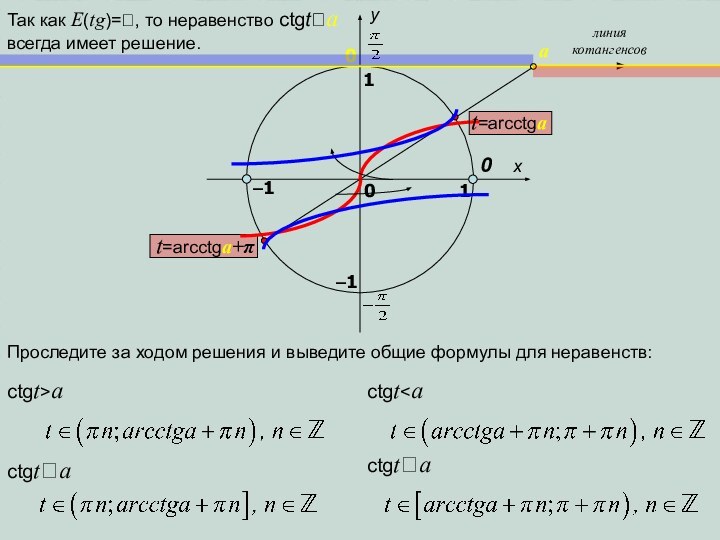
Проследите за ходом решения и выведите общие

xy101–10линия котангенсовa–1Проследите за ходом решения и выведите общие формулы для неравенств:Так

формулы для неравенств:
Так как E(tg)=, то неравенство сtgta всегда

имеет решение.

0

ctgt>a

ctgta

ctgt

ctgta



  • Имя файла: reshenie-prosteyshih-trigonometricheskih-neravenstv.pptx
  • Количество просмотров: 185
  • Количество скачиваний: 0
- Предыдущая Мой четвероногий друг
Следующая - Площадь прямоугольного треугольника

Похожие презентации

Презентация преобразование выражений содержащих степени с рациональным показателем Презентация преобразование выражений содержащих степени с рациональным показателем 197
Презентация по алгебре на тему Формула корней квадратного уравнения(8 класс) Презентация по алгебре на тему Формула корней квадратного уравнения(8 класс) 159
Прямоугольная система координат Прямоугольная система координат 192
Презентация по алгебре 9 класс Метод интервалов Презентация по алгебре 9 класс Метод интервалов 178
Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) 180
Исследование функции на монотонность и экстремумы Исследование функции на монотонность и экстремумы 138
Презентация для 8-9 класса Физико- математический турнир Презентация для 8-9 класса Физико- математический турнир 171
Презентация к уроку математики в 11 классе на тему Иррациональные уравнения Презентация к уроку математики в 11 классе на тему Иррациональные уравнения 170
Презентация к уроку Решение неравенств второй степени с одной переменной Презентация к уроку Решение неравенств второй степени с одной переменной 136
Теорема об отрезках пересекающихся хорд Теорема об отрезках пересекающихся хорд 234
Решение систем уравнений графическим способом Решение систем уравнений графическим способом 160
Математика і народознавство поруч. 8 клас, алгебра Математика і народознавство поруч. 8 клас, алгебра 143
Урок решения логарифмических неравенств Урок решения логарифмических неравенств 154
Свойства и график функции СИНУС Свойства и график функции СИНУС 177
Арифметическая прогрессия Арифметическая прогрессия 161
Элементы алгебры Элементы алгебры 202
Вероятность Вероятность 176
Первый урок алгебры в Первый урок алгебры в 157
Линейная функция Линейная функция 122
Арифметический квадратный корень Арифметический квадратный корень 81
Презентация по математики Взаимное расположение сферы и касательной(11 класс) Презентация по математики Взаимное расположение сферы и касательной(11 класс) 191
Решение кубических уравнений Решение кубических уравнений 237
Тригонометрическая форма записи комплексного числа 10 класс Тригонометрическая форма записи комплексного числа 10 класс 196
Презнтация по теме: Линейная функция Презнтация по теме: Линейная функция 148
Свойства числовых неравенств Свойства числовых неравенств 176
Презентация по алгебре по теме Решение тригонометрических уравнений Презентация по алгебре по теме Решение тригонометрических уравнений 210
Повторение курса алгебры за 7 класс. Повторение курса алгебры за 7 класс. 79
Конспект открытого урока по математике в 11 классе Конспект открытого урока по математике в 11 классе 150
Викторина по математике для учащихся 10-11 классов Хорошо-ли ты знаешь математику? Викторина по математике для учащихся 10-11 классов Хорошо-ли ты знаешь математику? 287
Решение дробных рациональных уравнений Решение дробных рациональных уравнений 144