событий.
Группа событий называется
полной, если при проведении
опыта всегда
происходитодно из этих событий.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





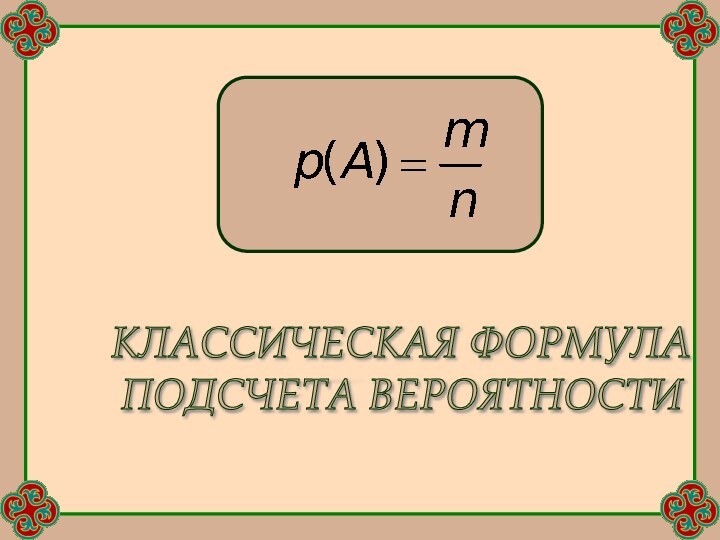





Пример.
Таким образом, вероятность любого события находится в интервале от 0 до 1.