Презентация на тему по математике по теме Формулы сокращённого умножения

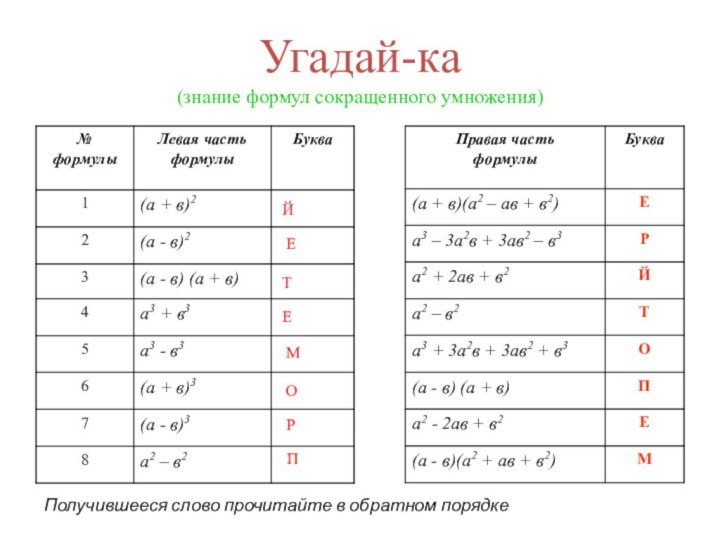
умножения были известны ещё около 4 тыс. лет тому

назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.
У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а²», а «квадрат на отрезке а», не аб а, «прямоугольник, содержащийся между отрезками а и б».
Некоторые термины подобного словесного изложения алгебры сохранились до сих пор. Так мы называем вторую степень числа квадратом, а третью степень – кубом числа.

выражений.
2. Уметь

применять эти формулы.
Задачи:
Обучающая: отработать навыки применения формул сокращенного умножения.
Развивающие:
Расширение кругозора учащихся.
Развитие приёмов умственной деятельности, памяти, внимания, умения сопоставлять, анализировать, делать выводы.
Повышение информационной культуры учащихся, интереса к предмету.
Развитие познавательной активности, положительной мотивации к предмету.
Развивать потребности к самообразованию.
Воспитательные:
Воспитание ответственности, самостоятельности, умения работать в коллективе.
Показать математику как интересную науку, превратить занятие в необычный урок, где может проявить себя каждый ученик.
Воспитание уважения друг к другу.

Декартом в его «Геометрии» (1637), правда, только для натуральных

степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676), трактовку которых к этому времени уже предложили Cтевин, Валлис и Жирар.

и физик. Создал основы аналитической геометрии, ввел понятие переменной

величины, разработал метод координат. Осуществил связь алгебры с геометрией.

Пьер Ферма (1601-1665) − французский математик, один из создателей аналитической геометрии и теории чисел. Занимался теорией решения алгебраических уравнений с несколькими переменными.

кроме единицы, есть разность двух квадратов.
Решение:
1 способ. (n+1)2 -

n2=(n+1-n)(n+1+n)=2n+1 - нечётное число
2 способ. (n+1)2 - n2 = n2+2n+1-n2=2n+1 - нечётное число

В школе Пифагора эта задача решалась геометрически. Действительно, если к квадрату со стороной n прибавить гномон, представляющий нечётное число 2n+1 (на рис. выделено цветом), то получится квадрат со стороной n+1,

т.е. n2 +(2n+1)=(n+1)2 или (n+1)2 – n2=2n+1

= a² - b²

(1)
(a + b)² = a² + 2ab +b² (2)
(a – b)² = a² - 2ab + b² (3)
(a + b) (a² - ab + b²) = a³ +b³ (4)
(a – b) (a² + ab + b²) = a³ - b³ (5)
(a + b)³ = a³ + 3a²b + 3ab² + b³ (6)
(a –b)³ = a³ - 3a²b + 3ab² - b³ (7)

трех слагаемых
Первый способ: алгебраическое умножение многочленов.
(a+b+c)*(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2== a2+ b2+c2+2ab+2ac+2bc.

Второй способ:

как сумма двух слагаемых в квадрате
((a+b)+c)2=(a+b)2+2(a+b)c+c2=a2+ c2+b2+2ab+2ac+2bc.

степень двух слагаемых
(a+b)4=(a+b)2(a+b)2=(a2+2ab+b2)(a2+2ab+b2)=
=a4+4a3b+6a2b2+4ab3+b4

Пятая степень суммы двух слагаемых:
(a+b)5=(a+b)2(a+b)3=(a2+2ab+b2)(a3+3a2b+3ab2+b3)==a5+5a4b+10a3b2+10a2b3+5ab4+b5

Строки

1
1 1
  1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1

Треугольник Паскаля

в)² = а² +2ав +в² для положительных а и

в.

После упрощения:

S=a2+ b2+c2+2ab+2ac+2bc.

число (до 10);
Умножьте его на себя;
Прибавьте к результату задуманное

число;
К полученной сумме прибавьте 1;
К полученному числу прибавьте задуманное число.

Скажите мне число, которое у вас получилось и
я отгадаю, какое число вы задумали.

Решение: x² + x + 1 + x = x² + 2x + 1 = (x + 1)²

Например, 5·5 + 5 + 1 + 5 = 36,
x = √36 – 1 = 6 – 1 = 5.

в виде 10а + 5.
Например, 25 = 2·10

+ 5.

Доказать, что для вычисления квадрата такого числа можно к произведению а(а + 1) приписать справа 25.
Например, 25² = 625, т.к. 2 ·(2 + 1) = 6.

Доказательство:
(10а + 5)² = 100a² + 100a + 25 =
= 100a(a +1) + 25 =
= a (a +1) ·100 + 25.
Найдите по этому правилу 45², 75², 115².

Т
Получившееся слово прочитайте в обратном порядке

Кто такой Прометей?
Что означает это имя?

За информацией обратиться:
www.google.ru
Поиск в

Интернете : Прометей

Результаты поиска:
http://mythology.sgu.ru/mythology/linc_personag/prometey.htm
http://ru.wikipedia.org/wiki/Прометей
http://greekroman.ru/prometheus.htm