- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему: Функция, её свойства и график.
Содержание
- 2. Цели уроказнакомство с понятием функции и ее свойств;совершенствование навыков чтения графиков;развитие интереса к предмету.
- 3. Задачи урокаобучающие:научить по графику функции находить область
- 4. Из истории возникновения функцииПонятие функции уходит своими
- 5. ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ 1646 – 1716 гг
- 6. Из истории возникновения функцииЛЕОНАРДО ЭЙЛЕР 1707 -
- 7. ХYxyу = f (x)Функцией называют такую зависимость
- 8. Способы задания функций1. Аналитический2. Графический3.
- 9. График функцииГрафиком функции называют множество всех точек
- 10. На графике показан процесс разогрева двигателя легкового
- 11. На рисунке жирными точками показано суточное количество
- 12. На графике показано изменение температуры воздуха в
- 13. Область определения функции Область значений функции
- 14. Все значения аргумента , при которых функция
- 15. Область значений функцииВсе значения, которые принимает функция(от англ. codomain «со-область»)Е(f)x01163-2yy = f(x) Е(f) = [-2;3]
- 16. МонотонностьСвойство графикаФункция возрастает[или убывает] на промежутке I,
- 17. ЗнакопостоянствоСвойство графикаПромежутки, на которых функция сохраняет постоянный
- 18. Нули функции-точки ,в которых функция обращается в
- 19. Назвать нули функции и наибольшее и наименьшее значения функции
- 20. 1 2 3 4
- 21. 1 2 3 4
- 22. 2 4 5
- 23. 1 2 3 4
- 24. 21 2 3 4
- 25. На каком из рисунков функция, заданная графиком, убывает на промежутке [0; 3]?3421ПОДУМАЙ!Верно! Проверка (4)ПОДУМАЙ!ПОДУМАЙ!xy01xy01xy01xy01
- 26. На каком из
- 27. 1433Функция у = f(x) задана на
- 28. Функция у = f(x) определена графиком. Укажите
- 29. Функция у = f(x) определена графиком. Укажите
- 30. На одном из следующих рисунков изображен график
- 31. ,,b = 0a ≥ 01.2.
- 32. Упражнение 1. Правило состоит в том, что
- 33. Подводится итог работычто нового вы узнали сегодня
- 34. Домашнее задание : 1.Знать основные понятия и
- 35. Скачать презентацию
- 36. Похожие презентации









![Презентация по математике на тему: Функция, её свойства и график. Область значений функцииВсе значения, которые принимает функция(от англ. codomain «со-область»)Е(f)x01163-2yy = f(x) Е(f) = [-2;3]](/img/tmb/6/593400/24c703fe6d95f8143fc272b1f62c423c-720x.jpg)
![Презентация по математике на тему: Функция, её свойства и график. МонотонностьСвойство графикаФункция возрастает[или убывает] на промежутке I, если для любого х Є](/img/tmb/6/593400/da673e422d35a7df6614b3650f86ea07-720x.jpg)


![Презентация по математике на тему: Функция, её свойства и график. На каком из рисунков функция, заданная графиком, убывает на промежутке [0; 3]?3421ПОДУМАЙ!Верно! Проверка (4)ПОДУМАЙ!ПОДУМАЙ!xy01xy01xy01xy01](/img/tmb/6/593400/44783980d67a3cdada418a6b4ec7f436-720x.jpg)
![Презентация по математике на тему: Функция, её свойства и график. 1433Функция у = f(x) задана на промежутке [-7; 8]. Укажите длину](/img/tmb/6/593400/6f53dcb5747e5ca859b4c3cdda83c601-720x.jpg)
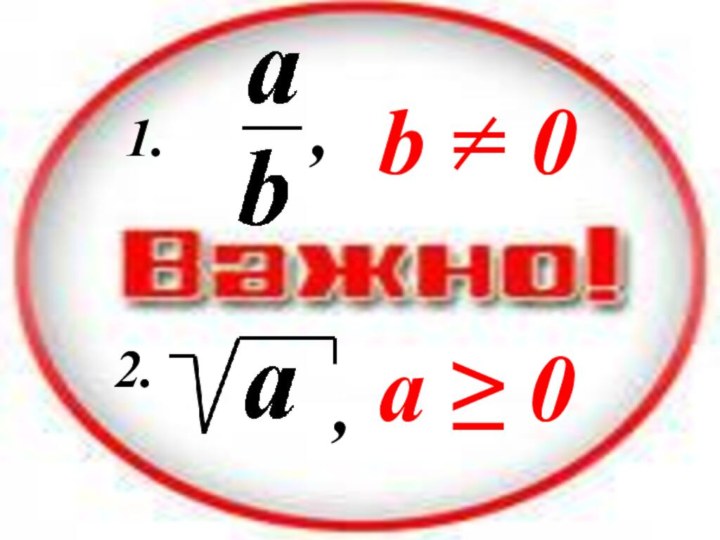




Слайд 2
Цели урока
знакомство с понятием функции и ее свойств;
совершенствование
навыков чтения графиков;
Слайд 3
Задачи урока
обучающие:
научить по графику функции находить область определения
функции , область значений функции , нули функции; промежутки
знакопостоянства , монотонность, наибольшее и наименьшее значения функции ;находить область определения и область значения функции, заданной формулой;
развивающие:
развивать интерес к предмету, познавательную и творческую деятельность студентов, математическую речь, память, внимание;
вырабатывать самостоятельность в освоении новых знаний.
воспитательные:
воспитывать у студентов ответственное отношение к учебному труду, волевые качества;
формировать эмоциональную культуру и культуру общения,
воспитывать чувство дружественной атмосферы в группе и умение работать самостоятельно.
Слайд 4
Из истории возникновения функции
Понятие функции уходит своими корнями
в ту далекую эпоху, когда люди впервые поняли, что
окружающие их явления взаимосвязаны.В ДРЕВНЕМ МИРЕ
Чем больше животных удастся убить на охоте, тем дольше племя будет избавлено от голода
Чем дольше горит костер, тем теплее будет в пещере.
Слайд 5
ГОТФРИД ВИЛЬГЕЛЬМ
ЛЕЙБНИЦ
1646 – 1716 гг
Из
истории возникновения функции
ГЕРМАНИЯ
Впервые употребил слово «функция»
В печати ввел
с 1694 года. Начиная с 1698 года ввел также термины «переменная» и «константа».
Слайд 6
Из истории возникновения функции
ЛЕОНАРДО ЭЙЛЕР
1707 - 1783
гг
Швейцарский, немецкий и российский математик и механик
В 1748
году дает окончательную формулировку определения функции: «Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых».
Слайд 7
Х
Y
x
y
у = f (x)
Функцией называют такую зависимость переменной
у от переменной х, при которой каждому значению переменной
х соответствует единственное значение переменной ух– независимая переменная,
аргумент
у – зависимая переменная,
функция
Слайд 8
Способы задания функций
1. Аналитический
2. Графический
3.
Табличный
4. Описательный
1. y=2x-5;
2.
3.
Функция на [-2; -1] возрастает,
на [0; 4] убывает,
на [-1; 0] равна 5.
Слайд 9
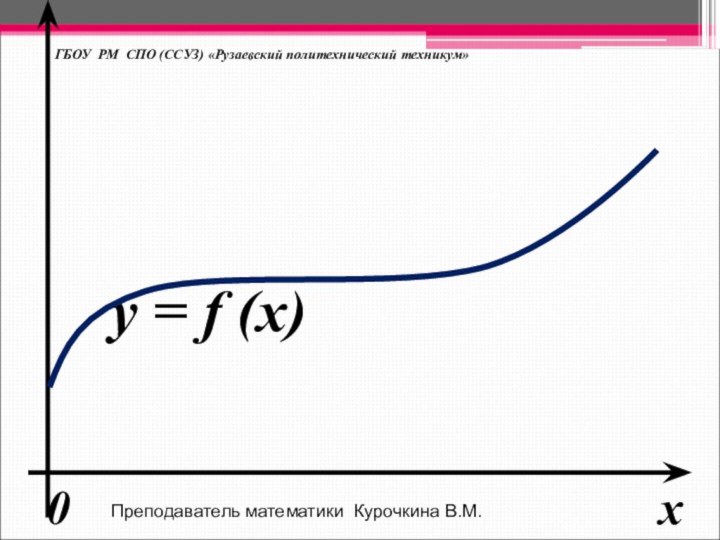
График функции
Графиком функции
называют множество всех точек координатной
плоскости,
абсциссы которых равны значениям аргумента,
а ординаты- соответствующим
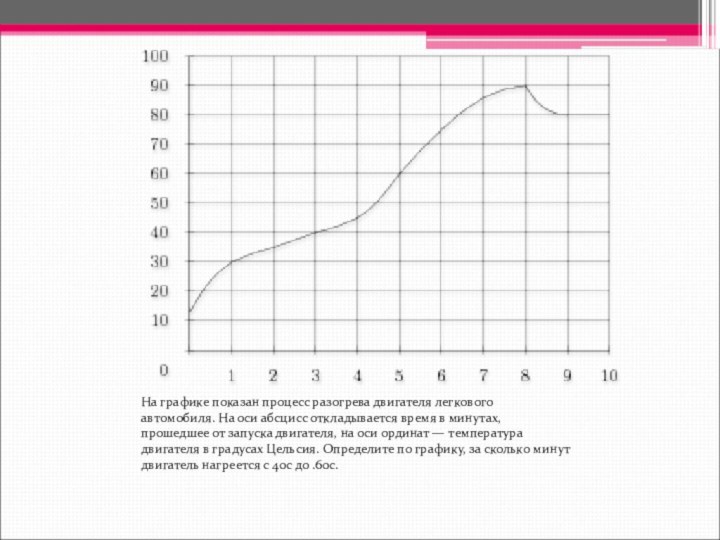
значениям функции.Слайд 10 На графике показан процесс разогрева двигателя легкового автомобиля.
На оси абсцисс откладывается время в минутах, прошедшее от
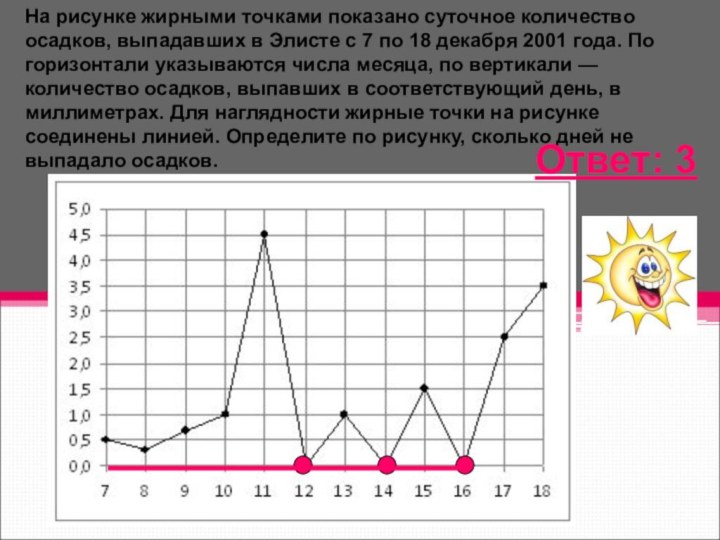
запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 40с до .60с.Слайд 11 На рисунке жирными точками показано суточное количество осадков,
выпадавших в Элисте с 7 по 18 декабря 2001
года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней не выпадало осадков.Ответ: 3
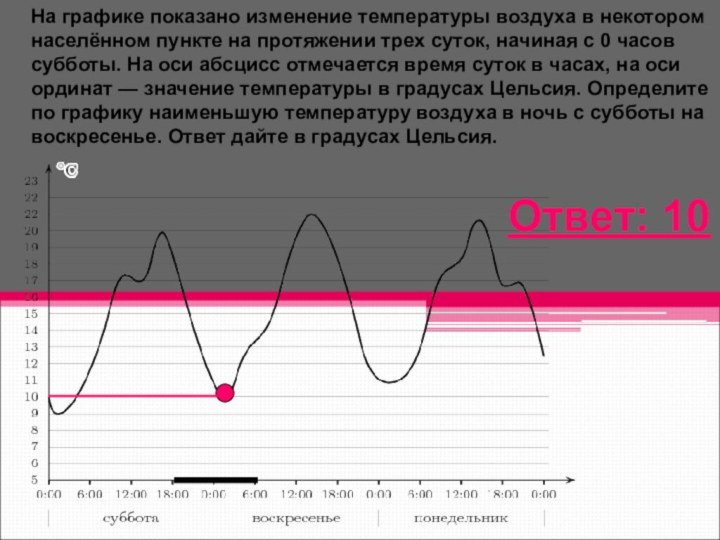
Слайд 12 На графике показано изменение температуры воздуха в некотором
населённом пункте на протяжении трех суток, начиная с 0
часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.Ответ: 10
Слайд 13
Область определения функции
Область значений функции
Монотонность
Промежутки
знакопостоянства,нули функции;
Наибольшее и наименьшее
значения функцииСвойства числовых функций
Слайд 14
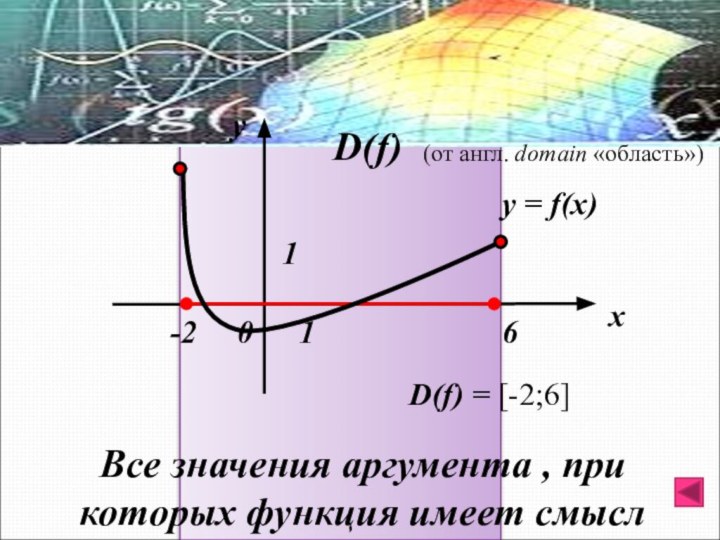
Все значения аргумента , при которых функция имеет
смысл
Область определения функции
D(f)
x
0
1
1
6
-2
y
y = f(x)
(от англ. domain «область»)
D(f)
= [-2;6]
Слайд 15
Область значений функции
Все значения, которые принимает функция
(от англ.
codomain «со-область»)
Е(f)
x
0
1
1
6
3
-2
y
y = f(x)
Е(f) = [-2;3]
Слайд 16
Монотонность
Свойство графика
Функция возрастает
[или убывает] на промежутке I, если
для любого х Є I выполняется условие :
при х1>х2
f(х1)>f(х2) [при х1>х2 f(х1)
Слайд 17
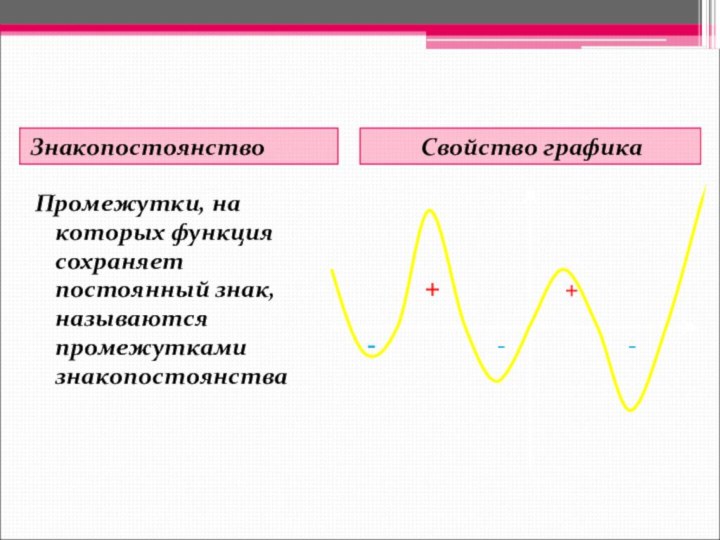
Знакопостоянство
Свойство графика
Промежутки, на которых функция сохраняет постоянный знак,
называются промежутками знакопостоянства
+
+-
-
-
Слайд 18
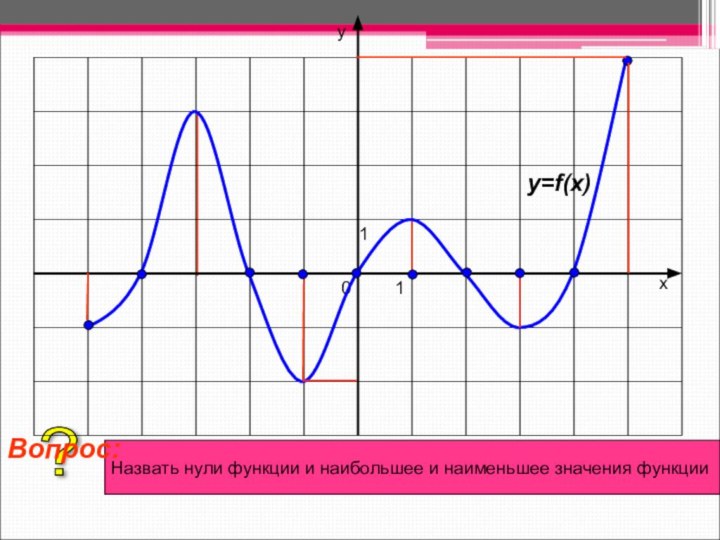
Нули функции-точки ,в которых функция обращается в нуль.
Наибольшее
и наименьшее значения функции – самое большое или самое
малое значение функции по сравнению со всеми возможными.
Слайд 20
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
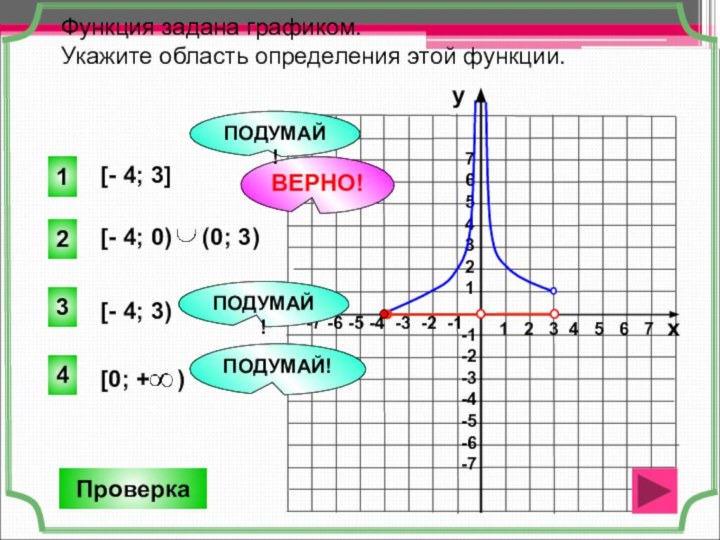
Функция задана графиком.
Укажите область определения этой функции.
[- 4; 3]
[- 4; 3)
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
у
х
Слайд 21
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите множество значений этой функции.
[1; 3]
[1; + ]
(-2; 4]
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
Слайд 22
2 4 5
-3
-2
3
2
0
- 1- 3
- 4
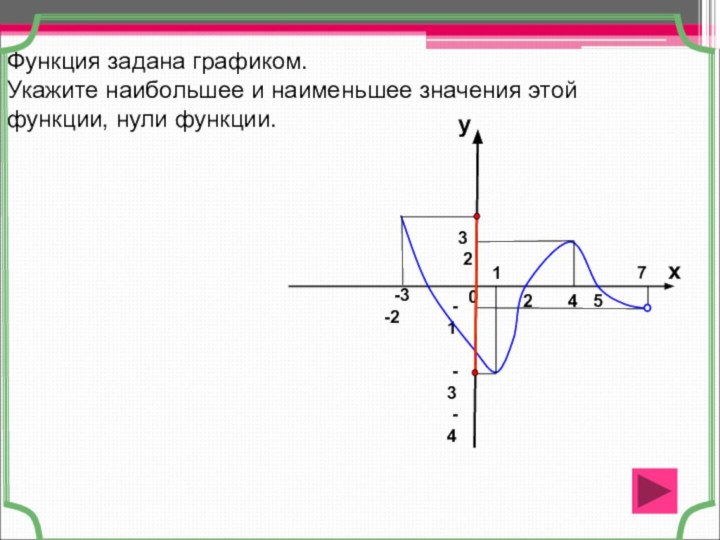
Функция задана графиком.
Укажите наибольшее и наименьшее значения этой функции, нули функции.
1 7
x
y
Слайд 23
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
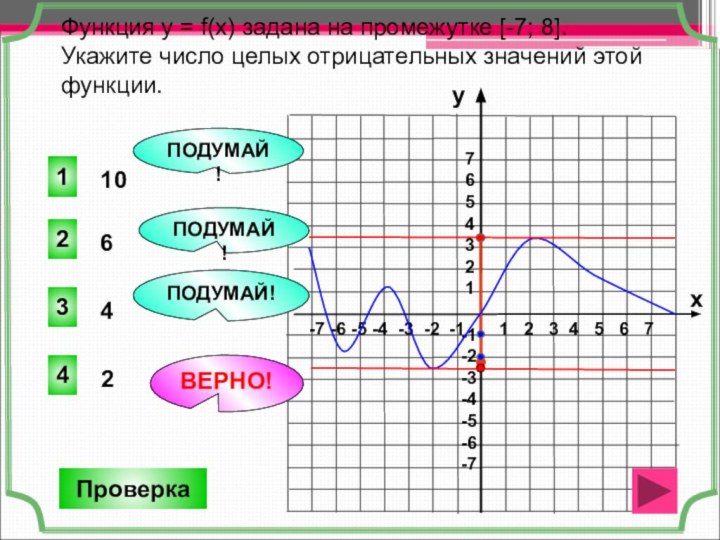
Функция y = f(x) задана на промежутке [-7; 8].
Укажите число целых отрицательных значений этой функции.
4
1
2
3
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
у
х
ВЕРНО!
2
4
6
10
Слайд 24
2
1 2 3 4 5
6 7
-7 -6 -5 -4 -3
-2 -17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
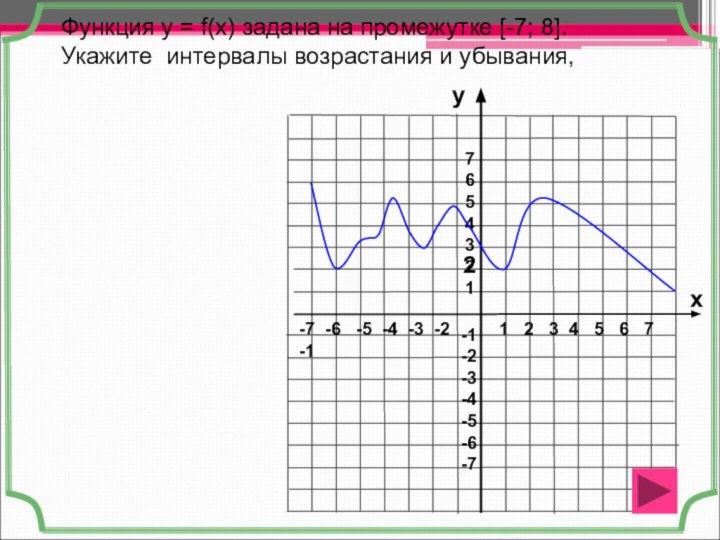
Функция y = f(x) задана на промежутке [-7; 8].
Укажите интервалы возрастания и убывания,
у
х
Слайд 25
На каком из рисунков функция, заданная
графиком, убывает
на промежутке [0; 3]?
3
4
2
1
ПОДУМАЙ!
Верно!
Проверка (4)
ПОДУМАЙ!
ПОДУМАЙ!
x
y
0
1
x
y
0
1
x
y
0
1
x
y
0
1
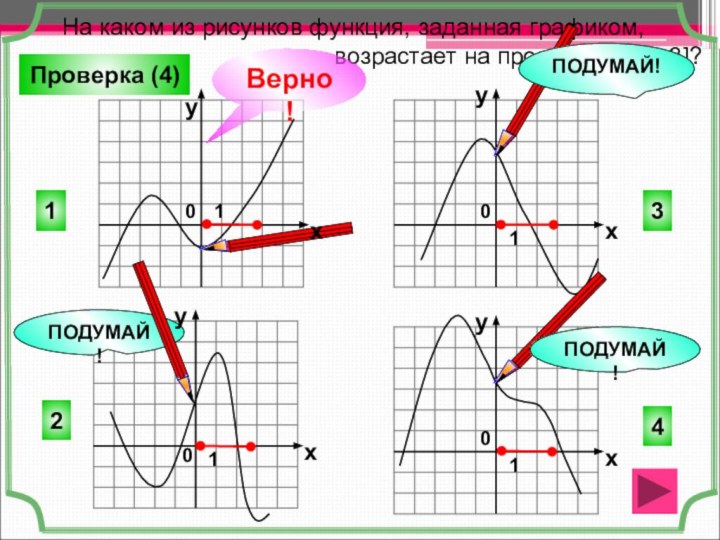
Слайд 26 На каком из рисунков
функция, заданная графиком,
возрастает на промежутке [0; 3]? 1
4
2
3
ПОДУМАЙ!
Верно!
Проверка (4)
ПОДУМАЙ!
ПОДУМАЙ!
x
y
0
1
x
y
0
1
x
y
0
1
x
y
0
1
Слайд 27
1
4
3
3
Функция у = f(x) задана на промежутке
[-7; 8].
Укажите длину промежутка возрастания этой функции.
Проверка
y =
f (x)
1 2 3 4 5 6 7 8
-7 -6 -5 -4 -3 -2 -1
y
x
5
4
3
2
1
-1
-2
-3
-4
2
11
8
Подумай!
Подумай!
Подумай!
Верно!
5
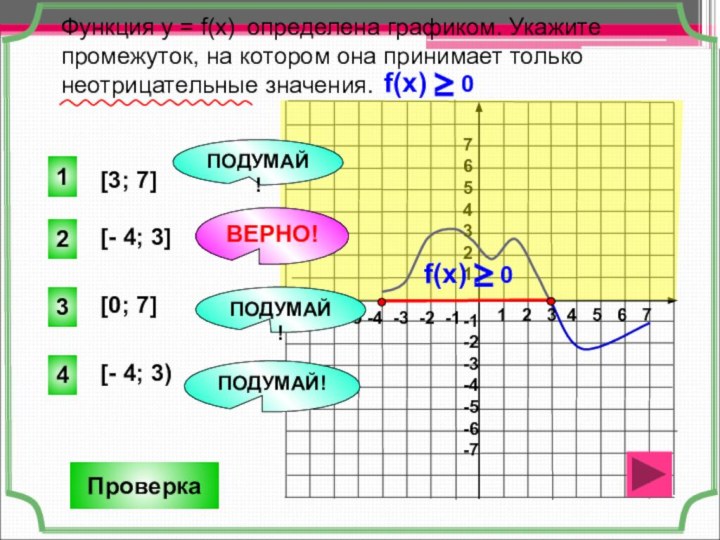
Слайд 28 Функция у = f(x) определена графиком. Укажите промежуток,
на котором она принимает только неотрицательные значения.
Проверка
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[- 4; 3]
2
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
[3; 7]
[0; 7]
[- 4; 3)
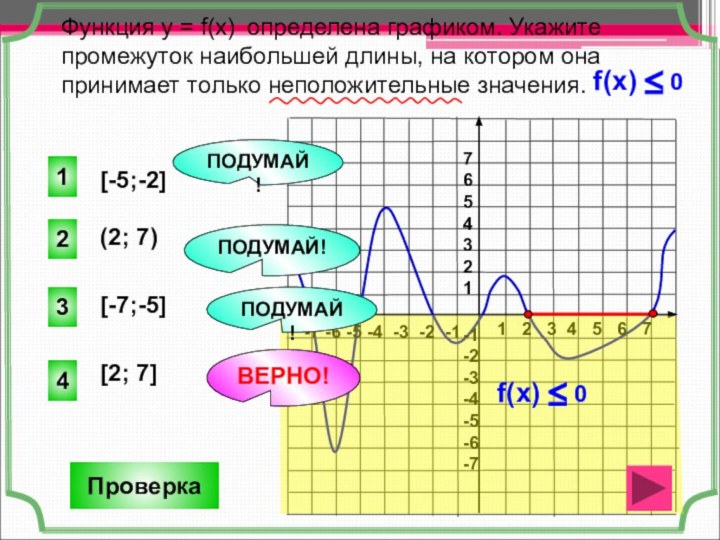
Слайд 29 Функция у = f(x) определена графиком. Укажите промежуток
наибольшей длины, на котором она принимает только неположительные значения.
Проверка
1
2 3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
(2; 7)
4
1
3
2
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
[-5;-2]
[-7;-5]
[2; 7]
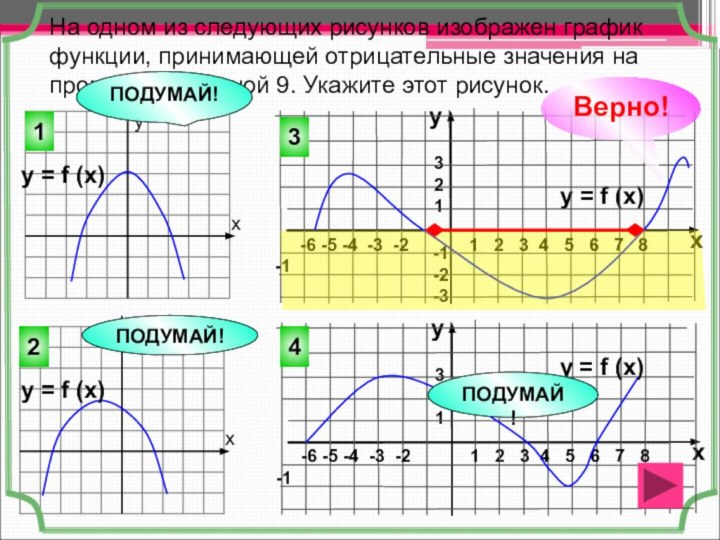
Слайд 30 На одном из следующих рисунков изображен график функции,
принимающей отрицательные значения на промежутке длиной 9. Укажите этот
рисунок.2
1
х
х
у
ПОДУМАЙ!
у
3
ПОДУМАЙ!
y = f (x)
y = f (x)
Верно!
ПОДУМАЙ!
4
Слайд 32 Упражнение 1. Правило состоит в том, что каждому
натуральному числу ставится в соответствие его произведение с числом
3 сложенное с числом 2.1) Требуется записать правило с помощью математических символов.
2) Найти множество определения.
3) Найти множество значений.
Указания к решению: f(n)=3*n+2, множество определения есть множество натуральных чисел, множество значений – множество натуральных чисел.
Упражнение 2. Правило состоит в том, что действительное число возводится в квадрат, затем из него вычитается число1 и извлекается квадратный корень.
1) Требуется записать правило с помощью математических символов.
2) Найти множество определения.
3) Найти множество значений.
Указания к решению: f(х)= ,множество определения есть , множество значений есть
Слайд 33
Подводится итог работы
что нового вы узнали сегодня на
уроке?
Подводится итог работы :
Что нового вы узнали сегодня на
уроке?Вспомним, имена каких ученых, связаны с понятием функции.
Что называется областью определения и областью значений функции?
Слайд 34 Домашнее задание : 1.Знать основные понятия и определения
по изученной теме.
2. Cоставить по 3 примера различного способа задания функции (аналитически и словесно).Дополнительный материал: подготовить сообщения на темы:
1. ФУНКЦИИ ВОКРУГ НАС (РАССКАЗ О ЗНАЧЕНИИ ФУНКЦИИ В ЖИЗНИ ЧЕЛОВЕКА
2. ФУНКЦИИ В ФИЗИКЕ И ГЕОМЕТРИИ