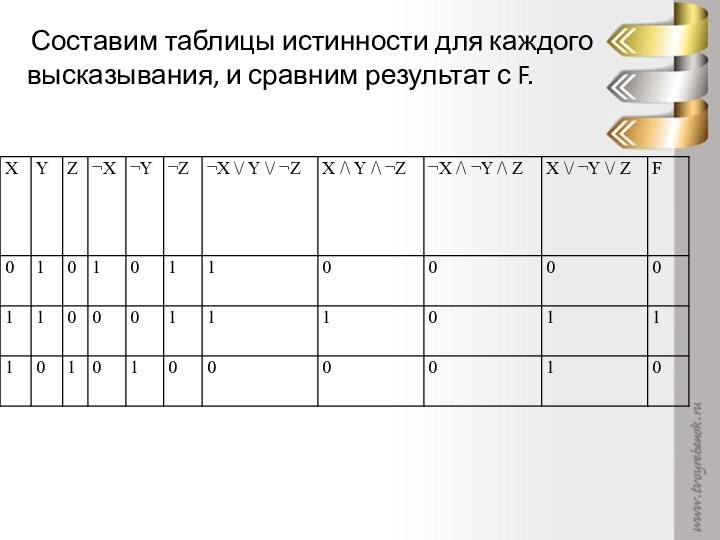
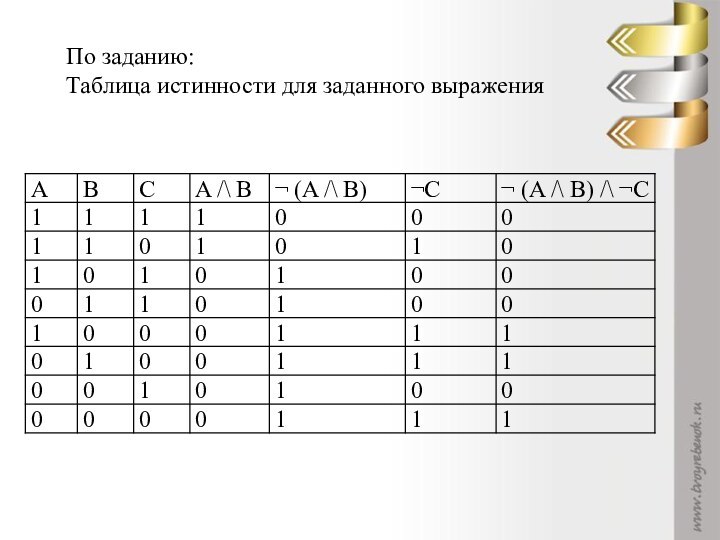
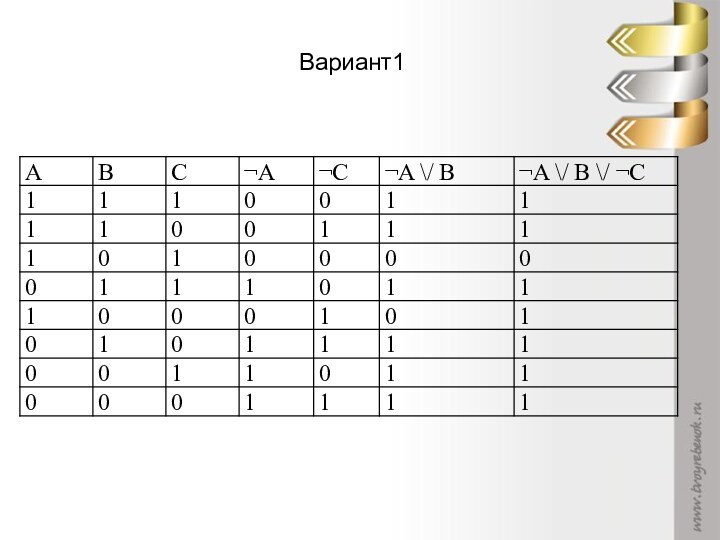
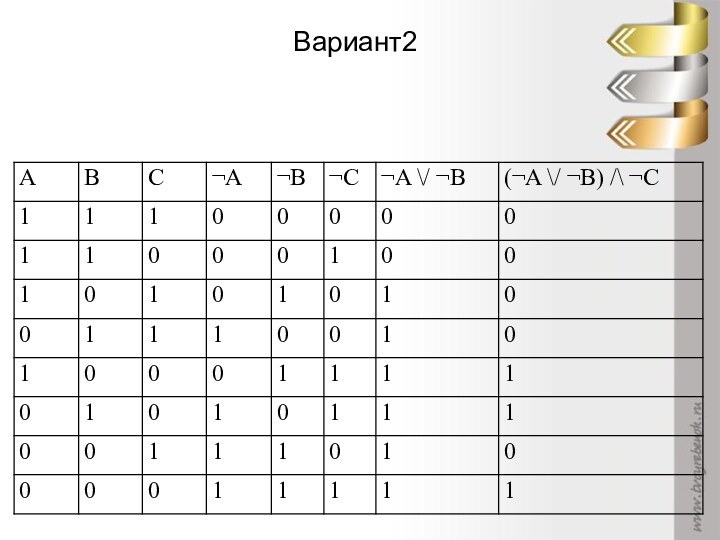
сложное высказывание?
Сколько Вы знаете базовых логических операций?
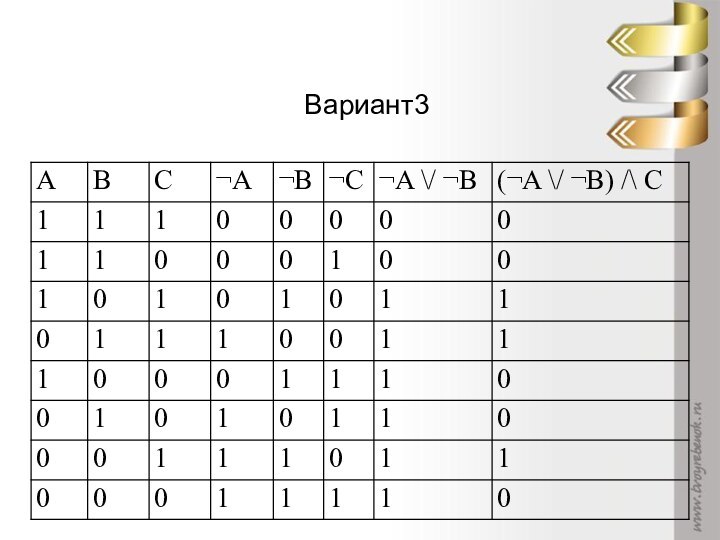
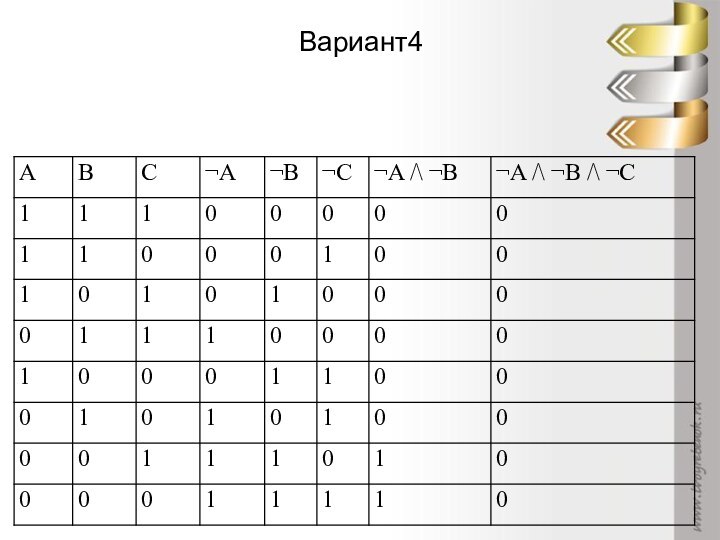
Перечислите названия базовых логических операцийДля чего нужна таблица истинности?
Повторение пройденного материала