Слайд 2
Определения
Равенство с переменной g(x) = f(x) называется уравнением
с одной переменной х.
Всякое значение переменной, при котором
f(x) и g(x) принимают равные числовые значения, называется корнем уравнения.
Решить уравнение - это значит найти все его корни или доказать, что их нет.
Слайд 3
Равносильные уравнения
Уравнения, имеющие одни и те же корни,
называются равносильными.
Равносильными считаются и уравнения, у которых нет
корней.
Например, уравнения х + 2 = 5 и х + 5 = 8 равносильны;
уравнения x2 + 5 = 0 и 3x2 + 1 = 0 равносильны, так как корней не имеют.
Слайд 4
Теорема 1
Если в уравнении какое-нибудь слагаемое перенести из
одной части в другую, изменив его знак, то получится
уравнение, равносильное данному.
Слайд 5
Теорема 2
Если обе части уравнения умножить или разделить
на одно и то же отличное от нуля число,
то получится уравнение, равносильное данному.
Слайд 6
Линейные уравнения
Линейным уравнением с одной переменной х называют
уравнение вида ax = b, где a,b ∈ R;
а называют коэффициентом при переменной, b - свободным членом.
Слайд 7
Три случая для линейного уравнения ax = b
1) а № 0; в этом случае корень равен
b/a;
2) а = 0, b = 0; в этом случае уравнение принимает вид 0Ч х = 0, что верно при любом х, т. е. корнем уравнения является любое действительное число;
3) а = 0, b № 0; в этом случае уравнение принимает вид 0Ч х = b, оно не имеет корней.
Слайд 8
Квадратное уравнение
Квадратным уравнением называется уравнение вида
ax2+bx+c=0,
где a, b, с ∈ R (a ≠ 0).
Числа a, b, с носят следующие названия: a - первый коэффициент, b - второй коэффициент, с - свободный член.
Слайд 9
Дискриминант
Выражение D=b2–4ac называется дискриминантом квадратного уравнения.
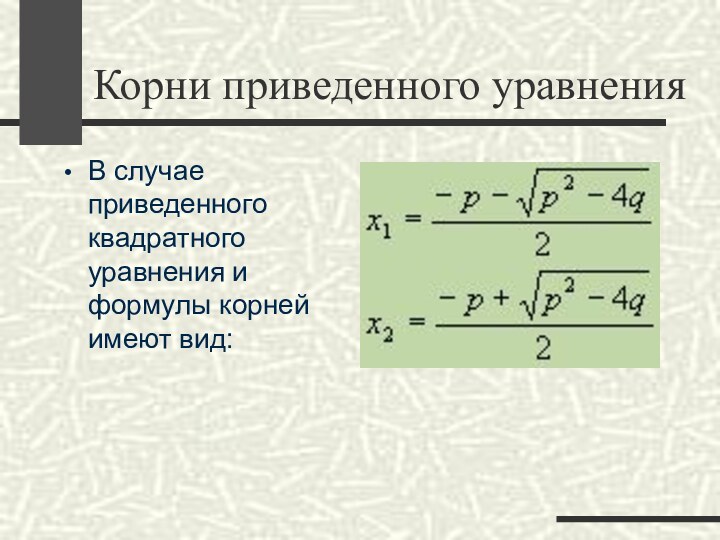
Если а
= 1, то квадратное уравнение вида x2+px+q=0 называется приведенным,
а его дискриминант D=p2–4q.
Слайд 10
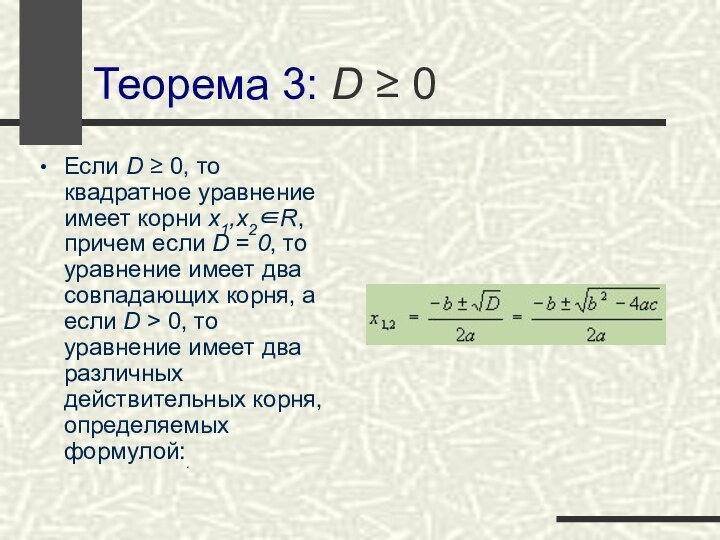
Теорема 3: D ≥ 0
Если D ≥ 0,
то квадратное уравнение имеет корни x1,x2∈R, причем если D
= 0, то уравнение имеет два совпадающих корня, а если D > 0, то уравнение имеет два различных действительных корня, определяемых формулой:.
Слайд 11
Теорема 3: D < 0
Если D < 0,
то квадратное уравнение не имеет действительных корней.