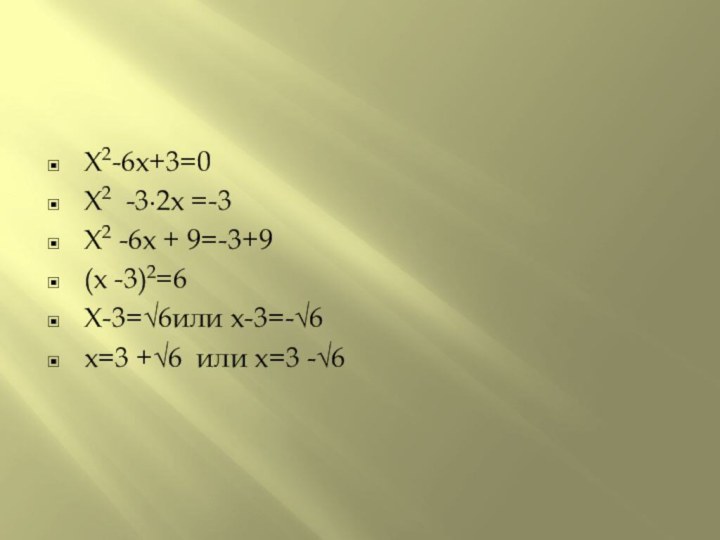; 3) x2- 25=0; 4) 4x2- 16=0;
5) x2+1=0
2.Найти
такое положительное число m, чтобы данное выражение было квадратом суммы или разности:x2+ 4x + m ; x2+ 16x + m; ; x2+ mx + 4; ;
x2-mx + 9
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть