Презентация на тему Вычисление производной

с применением интерактивной доски. Продолжительность 15 минут. На данном

уроке рассматриваются вопросы, способствующие:
-закреплению навыков вычисления производной,
- развитию умений выделять главное,
логически излагать мысли.
Урок рассчитан на творческую деятельность учащихся.

урока:
«Вычисление производной»
Цель урока: закрепление знаний по теме «Производная».

Информационно-коммуникационная технология

Тип

урока: урок закрепления знаний, умений и навыков

Форма урока: работа в малой группе.

Технические средства обучения: интерактивная доска, компьютер

теоретических вопросов темы;
обобщить умения и навыки учащихся при вычислении

производной;

развивать интеллектуальную, рефлексивную культуру,
навыки самостоятельной деятельности, навыки самоконтроля учащихся;

воспитывать культуру умственного труда, умение давать самооценку.

Предполагаемые результаты обучающихся:
знать и уметь применять правила дифференцирования,
формулы вычисления производных линейной, степенной,
тригонометрических функций.

И. Есенова, З. А. Жумагулова «Алгебра и начала анализа»,

10 класс
Сборник задач по алгебре.
Учебное пособие для 10-классов естественно-математического направления общеобразовательных школ.
3. Старцева Н.А. Применение электронных пособий на уроках математики // Информационные технологии в образовании. Сб. научно - методических материалов, Новосибирск: НГУ, - 2004

(1844–1924) заметил: «Что учиться можно только весело... Чтобы переварить

знания, надо поглощать их с аппетитом». Последуем совету писателя: будем на уроке активны, внимательны. Перед нами стоит задача: повторить и закрепить правила вычисления производных, формулы производной сложной, степенной и тригонометрических функций. Сегодняшний урок пройдет с использованием презентаций.
2. Активизация знаний.
Устная разминка, повторение правил вычисления производных
(слайд №1)
3. Практическая часть.
Работа по таблице у интерактивной доски на тему «Производные» (решение примеров)
4. Проверка творческого домашнего задания. Историческая справка о создании теории производной (оформить в виде презентации -
слайд №2,3)
5. Домашнее задание. Подготовить презентацию на тему: « Применение производной к исследованию функции».
6. Рефлексия. Самооценка учащихся.

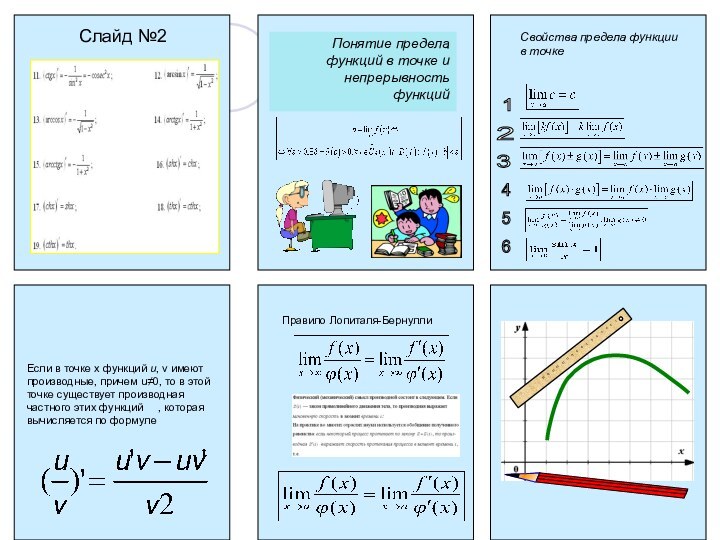
тригонометрических функций
(sinx)'=cosx
(cosx)'=-sinx
(ctgx)'=-1/sin²x
(tgx)'=1/cos²x
Можно найти по формуле

Физический смысл

производной

В задаче о мгновенной скорости каждому t соответствует свое значение мгновенной скорости, т.е. производная от пути по времени есть скорость

В общем случае, производная – это скорость изменения функции.

Если функция f(x) имеет производную в точке x, то эта функция называется дифференцируемой в этой точке.

Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке.

Операция нахождения производной называется дифференцированием.

у

y=f(x)

x

h

Физический смысл производной

Производную сложной функции

функций
Свойства предела функции в точке
1
2
3
4
5

6

Если в точке х функций u, v имеют производные, причем u≠0, то в этой точке существует производная частного этих функций , которая вычисляется по формуле

Правило Лопиталя-Бернулли

веков ознаменовались огромным интересом ученых к объяснению движения и

нахождению законов, которым оно подчиняется.
Как никогда остро встали вопросы об определении и вычислении скорости движения и его ускорения. Решение этих вопросов привело к установлению связи между задачей о вычислении скорости движения тела и задачей проведения касательной к кривой, описывающей зависимость пройденного расстояния от времени.

Общее понятие производной было сделано независимо друг от друга почти одновременно

английским физиком и математиком И.Ньютоном

немецким философом и математиком Г.Лейбницем.

и

Слайд №3