Презентация на тему Урок математики по теме Решение логарифмических уравнений и неравенств

навыков и умений по теме.
Задачи:
- повторить определение логарифма, основное

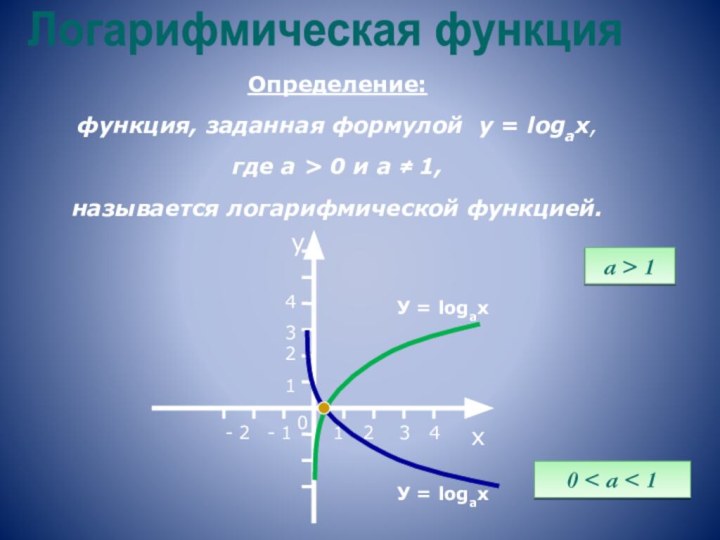
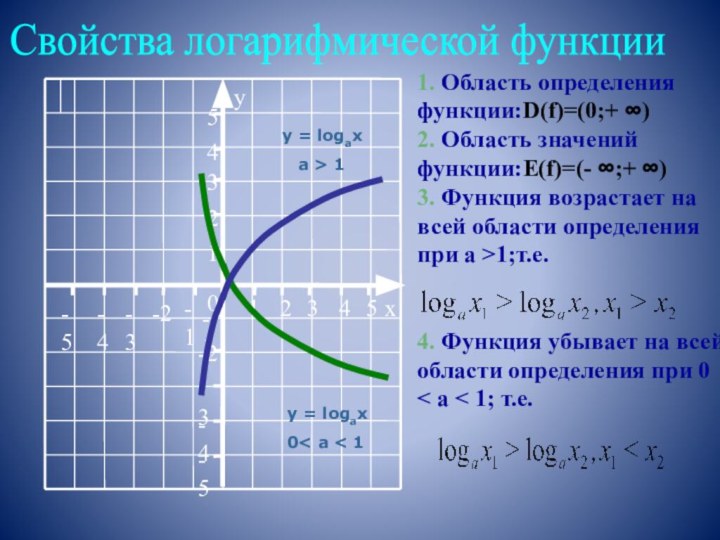
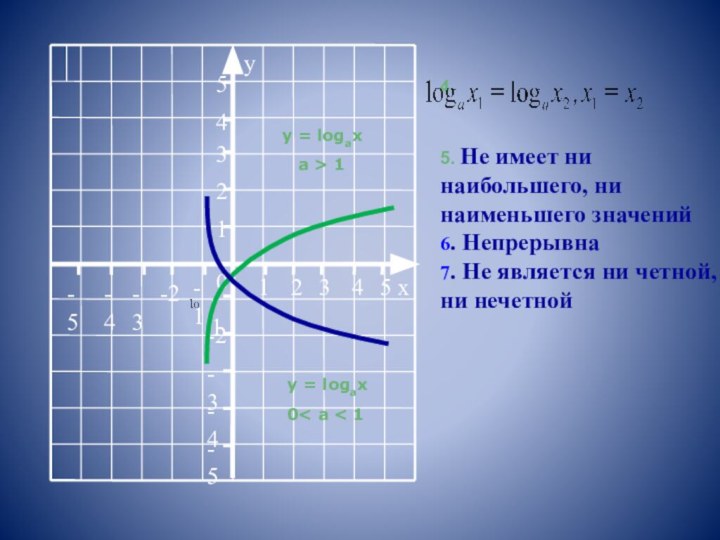
логарифмическое тождество, простейшие свойства логарифмов, определение и свойства логарифмической функции;
- закрепить способы решения логарифмических уравнений и неравенств;
- развивать вычислительные навыки, навыки самостоятельной работы, самоконтроля, навыки работы с различными источниками информации, а также познавательный интерес к предмету и логическое мышление;
- воспитывать информационную культуру учащихся, аккуратность, дисциплинированность.
Оборудование: компьютер, мультимедийный проектор, Интернет-ресурсы.

не равному единице основанию a называется показатель степени, в

которую нужно возвести основание a, чтобы получить число b:

loga b=x, ax =b, где а > о, а ≠ 1, b >0, x Є R,

Основное логарифмическое тождество

основанию а равен нулю:
при x>0 и y>0

2. Логарифм а по основанию а равен 1:
logaa =1

3. Cумма логарифмов равна логарифму произведения :
logaх + logaу = loga(xy),
4. Разность логарифмов равна логарифму частного:
logaх - logaу = loga(x/y), x>0 и y>0

логарифм основания этой степени:
logaxp =plogax , х>0

для любого

действительного числа р.
6.



для любых действительных m и n

7. Формула перехода от одного основания логарифма к другому основанию:





8.

а > 0 и а  1,
называется логарифмической

функцией.

a > 1

0 < a < 1

У = logax

У = logax

> 1
y = logax
0< a < 1
1.

Область определения функции:D(f)=(0;+ )
2. Область значений функции:E(f)=(- ;+ )
3. Функция возрастает на всей области определения при а >1;т.е.


4. Функция убывает на всей области определения при 0 < а < 1; т.е.

= logax
0< a < 1
4.


5. Не имеет

ни наибольшего, ни наименьшего значений
6. Непрерывна
7. Не является ни четной, ни нечетной

(убрать логарифмы)
Логарифмирование
Введение новой переменной (приведение к квадратному уравнению)
Графический

живой».