- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Význam hodnocení podniku a podnikatelských aktivit
Содержание
- 2. Osnova přednáškyVýznam hodnocení podniku a podnikatelských aktivitMetody používané v ekonomických analýzách
- 3. Ad 1) Význam hodnocení podniku a podnikatelských aktivit
- 4. Schéma: Význam hodnocení podnikatelské činnostiKdo má zájem na výsledku hodnocení podnikuHodnocení podnikuprosperitahodnotavlastnícimanagementzaměstnancistát/EUdodavateléodběrateléinvestořiveřejnostvěřitelé/banky
- 5. Ad 2) Metody používané v ekonomických analýzáchEkonomická
- 6. Technická analýza
- 7. Ad 1. 1. 1. 1. HORIZONTÁLNÍ ANALÝZA
- 8. Ad 1. 1. 1. 2. VERTIKÁLNÍ ANALÝZA (procentní rozbor)- slouží k posouzení struktury agregovaného jevu
- 9. Ad 1. 1. 2. ANALÝZA POMĚROVÝCH VELIČINnejoblíbenější
- 10. Ad 1. 2. ANALÝZA SOUSTAV UKAZATELŮHIERARCHICKÉ (1.
- 11. Ad 1. 2. 1. PYRAMIDÁLNÍ SOUSTAVY UKAZATELŮnejčastěji
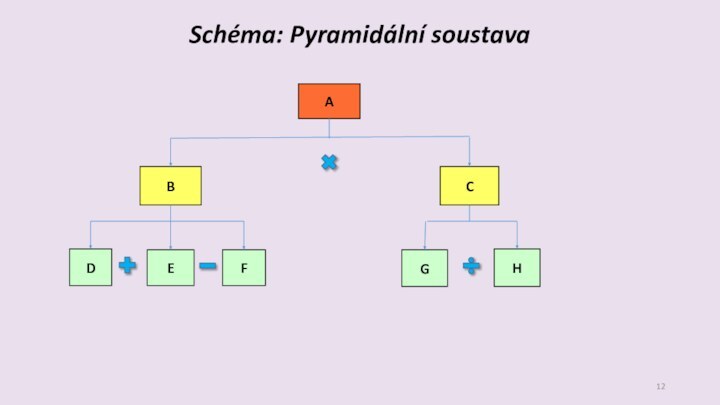
- 12. Schéma: Pyramidální soustavaABCEDFGH
- 13. - mezi dílčími ukazateli v pyramidě existují
- 14. Vliv dílčích ukazatelů na vrcholový ukazatel při
- 15. vliv dílčích ukazatelů na vrcholový ukazatel je
- 16. Ad b) vliv relativních změn vliv dílčích
- 17. PŘ: Ve struktuře CELKOVÉHO KAPITÁLU aplikujte vliv:
- 18. PŘ: výsledkyad a) vliv absolutních změn173 632
- 19. Vliv dílčích ukazatelů na vrcholový ukazatel při
- 20. Ad 1) Metoda postupných změnprincip: pouze tam,
- 21. Ad2) Metoda rozkladu se zbytkemprincip: pouze tam,
- 22. Ad3) Metoda logaritmická (metoda logaritmu indexu
- 23. Ad4) Funkcionální metoda princip: může se používat
- 24. 2. kvantifikace vlivu dílčích ukazatelů na vrcholový
- 25. PŘ: Aplikujte vliv změn dílčích ukazatelů (rentabilita
- 26. PŘ: výsledkyad a) metoda rozkladu s postupnými
- 27. Du Pontův rozklad – nejznámější pyramidová soustavaČistý zisk/vlastní kapitálČistý zisk/aktivaAktiva/vlastní kapitálZisk/tržbyTržby/aktivaČistý zisktržbyČisté tržbyaktivatržby∑NOAdl. M
- 28. Technická analýza
- 29. Analýza soustav ukazatelů → Ploché
- 30. BONITNÍ MODELYdiagnostickéhodnotí podnik jedním syntetickým koeficientem, který
- 31. Kralicekův „Rychlý test“navržen v r. 1990rychlost a
- 32. Tabulka: Stupnice hodnocení ukazatelů
- 33. BANKROTNÍ MODELYpredikčnípředpovídají případné ohrožení finančního zdraví podnikuanalýza
- 34. Altmanova formule bankrotu (Z-skóre)vychází z diskriminační analýzy
- 35. Скачать презентацию
- 36. Похожие презентации
Osnova přednáškyVýznam hodnocení podniku a podnikatelských aktivitMetody používané v ekonomických analýzách
































Слайд 2
Osnova přednášky
Význam hodnocení podniku a podnikatelských aktivit
Metody používané
v ekonomických analýzách
Слайд 4
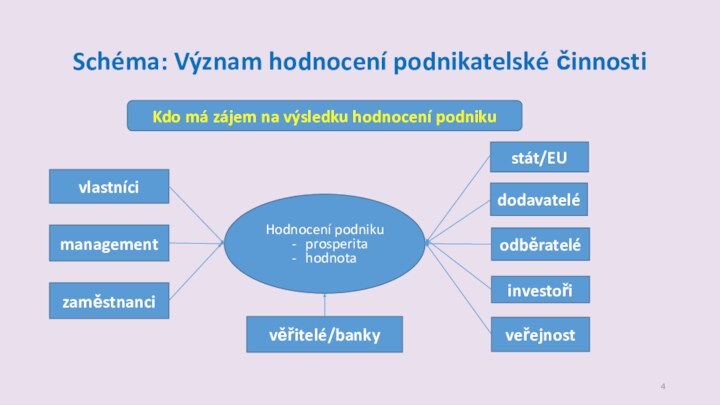
Schéma: Význam hodnocení podnikatelské činnosti
Kdo má zájem na
výsledku hodnocení podniku
Hodnocení podniku
prosperita
hodnota
vlastníci
management
zaměstnanci
stát/EU
dodavatelé
odběratelé
investoři
veřejnost
věřitelé/banky
Слайд 5
Ad 2) Metody používané v ekonomických analýzách
Ekonomická analýza
– rozklad určitého ekonomického celku (jevu, procesu) na dílčí
části, jejich podrobné zkoumání, hodnocení a určení možností jejich zlepšení; a následně opětovná skladba do upraveného celku s cílem: zlepšit jeho fungování a zvýšit výkonnost.Analýza – členění:
z hlediska věcného - fundamentální
- technická
b) z hlediska časového - ex-ante
- ex-post
Слайд 7 Ad 1. 1. 1. 1. HORIZONTÁLNÍ ANALÝZA
(analýza trendů)
- sleduje
vývoj položek finančních výkazů v čase, tj. změnu určité položky:absolutní změnou = hodnotat – hodnotat-1
procentní změnou = (absolutní změna/hodnotat-1 ) x 100(%)
indexem - řetězovým: rT = xT/xT-1
- bazickým: bT = xT/x0
Слайд 8
Ad 1. 1. 1. 2. VERTIKÁLNÍ ANALÝZA
(procentní rozbor)
-
slouží k posouzení struktury agregovaného jevu
Слайд 9
Ad 1. 1. 2. ANALÝZA POMĚROVÝCH VELIČIN
nejoblíbenější a
nejrozšířenější forma ukazatelů
umožňují komparativnost mezi firmami i ve firmě
v časemohou být - podílové
- vztahové
Слайд 10
Ad 1. 2. ANALÝZA SOUSTAV UKAZATELŮ
HIERARCHICKÉ (1. 2.
1. Pyramidální soustavy ukazatelů)
jsou řazeny sestupně podle významu (⇒
tvar pyramidy)všechny ukazatele nemohou být předem účelově vybírány, vyplynou z existujících vztahů)
význam ukazatelů je dán jeho postavením v pyramidě
PLOCHÉ (1. 2. 2. Ploché soustavy ukazatelů)
mají tvar rovnice (př. Bonitní a bankrotní modely)
ukazatele jsou účelově vybírány
význam ukazatele je dán jejich vahou
Слайд 11
Ad 1. 2. 1. PYRAMIDÁLNÍ SOUSTAVY UKAZATELŮ
nejčastěji používané
soustavy ukazatelů
souhrnně znázorňují najednou několik charakteristik finančního zdraví podniku
a umožňují zjišťovat vzájemné souvislosti mezi souhrnnou veličinou a dílčími charakteristikami a mezi charakteristikami navzájemprincipem konstrukce je postupný rozklad vrcholového ukazatele na ukazatele dílčí.
Každý jednotlivý dílčí ukazatel je výsledkem působení řady dalších činitelů, které mají k němu opět příčinný vztah. Dílčí ukazatel tak zaujímá pozici vrcholového ukazatele a je možné ho opět rozložit do řady dílčích ukazatelů 2. stupně atd. ⇒ tím vzniká podoba pyramidy, kdy ukazatele nižších stupňů vystupují jako příčiny (činitelé) ovlivňující ukazatele úrovně bezprostředně vyšší.
Слайд 13
- mezi dílčími ukazateli v pyramidě existují vzájemné
vazby:
matematické (aditivní; multiplikativní)
ekonomické
Řešení pyramidálních soustav:
Volba syntetického – vrcholového
ukazateleRozklad na ukazatele vyšších řádů – analytické ukazatele
Kvantifikace vlivů dílčích ukazatelů na ukazatel vrcholový
Interpretace výsledků
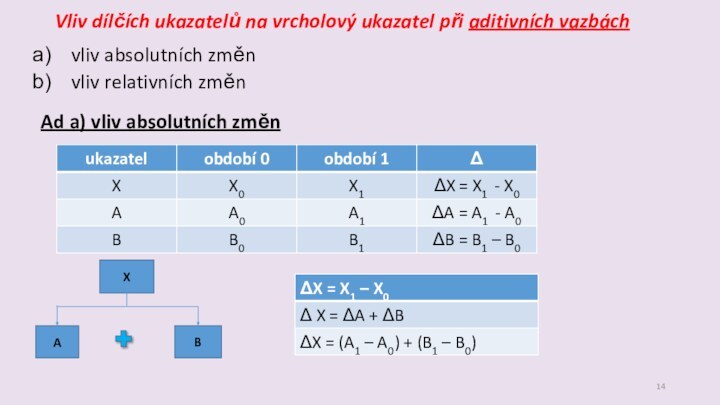
Слайд 14 Vliv dílčích ukazatelů na vrcholový ukazatel při aditivních
vazbách
vliv absolutních změn
vliv relativních změn
Ad a) vliv absolutních změn
X
A
B
Слайд 15
vliv dílčích ukazatelů na vrcholový ukazatel je dán:
u
součtových vazeb součtem jejich absolutních změn
u rozdílových vazeb rozdílem
jejich absolutních změn
Слайд 16
Ad b) vliv relativních změn
vliv dílčích ukazatelů na
vrcholový ukazatel je dán 2 charakteristikami, a to:
podílem dílčího
ukazatele na vrcholovém ukazateliindexem změny dílčího ukazatele
ΔX = iA . A0/X0 + iB . B0/X0
ΔX = A1/A0 . A0/X0 + B1/B0 . B0/X0
Слайд 17 PŘ: Ve struktuře CELKOVÉHO KAPITÁLU aplikujte vliv: a) absolutních
změn jeho dílčích složek, tj. vlastního kapitálu a cizího
kapitálu b) relativních změn jeho dílčích složek, tj. vlastního kapitálu a cizího kapitálu
Слайд 18
PŘ: výsledky
ad a) vliv absolutních změn
173 632 =
-36 255 + 209 887
ad b) vliv relativních změn
1,2239
= 0,3031 + 0,9208Слайд 19 Vliv dílčích ukazatelů na vrcholový ukazatel při multiplikativních
vazbách
Při řešení soustav se mohou aplikovat 4 metody:
Metoda postupných
změnMetoda rozkladu se zbytkem
Metoda logaritmická
Metoda funkcionální
X
A
B
Слайд 20
Ad 1) Metoda postupných změn
princip: pouze tam, kde
je syntetický ukazatel výsledkem součinu analytických ukazatelů
postup: mění se
vždy jeden z ukazatelů a ostatní zůstávají nezměněnyΔX/ΔB = ΔB . A0
ΔX/ΔA = ΔA . B1
přednosti: jednoduchost
nedostatky:
- není reálné, aby se jeden faktor měnil a ostatní zůstaly nezměněny
- nepřesnost, protože výsledek závisí na pořadí, ve kterém faktory měníme
Слайд 21
Ad2) Metoda rozkladu se zbytkem
princip: pouze tam, kde
je syntetický ukazatel výsledkem součinu analytických ukazatelů
postup: mění se
každý ukazatel individuálně, při konstantní hodnotě ostatních ukazatelů (shoda s metodou postupných změn) a přidává se vliv změny všech ukazatelů najednouΔX/ΔB = ΔB . A0
ΔX/ΔA = ΔA . B0
ΔX/ΔA ΔB = ΔA . ΔB
přednosti: jednoduchost, snaha vyjádřit i souhrnný vliv ukazatelů
nedostatky: nepřesnost, špatná interpretace „zbytku“
Слайд 22
Ad3) Metoda logaritmická
(metoda logaritmu indexu hodnot)
princip: - vychází
z indexu změn analytických ukazatelů
- použití je tam, kde
ukazatele nemají zápornou hodnotupoužití jen tam, kde ukazatele nemají nulovou hodnotu
postup:
ΔX = X1 - X0
X1 - X0 = X0 . (a1/a0 . b1/b0) - X0
(X1 - X0 )/X0 = a1/a0 . b1/b0
Aplikace logaritmického počtu:
X/A = (log a1/a0 / log X1/X0) . ΔX
X/B = (log b1/b0 / log X1/X0) . ΔX
přednosti: přesnost, není citlivá na pořadí ukazatelů
nedostatky: náročnost na výpočet, problémy při aplikaci podílových vazeb (tam se musí stanovit reciproký ukazatel a nahradit vazbu podílovou vazbou součinovou)
Слайд 23
Ad4) Funkcionální metoda
princip:
může se používat všeobecně
(i u záporných hodnot)
přiřazuje změnu syntetického ukazatele k jednotlivým
analytickým ukazatelům dělením (výchozí hodnotou)postup:
1. vydělení dílčích ukazatelů výchozí hodnotou
Δ X = a1 b1 – a0 b0 a1b1 = (a0 + Δa) . (b0 + Δb)
= a 1b1 . a0 b0 - a0 b0
a0b0
= a0b0 (a1 b1 – 1 )
a0b0
Слайд 24
2. kvantifikace vlivu dílčích ukazatelů na vrcholový rovněž
pomocí výchozí hodnoty
ΔX = ΔXa + ΔXb + ΔXaΔXb
ΔXa
= X0 ( ΔXa + ΔXa ΔXb) = X0 (Δa + Δa Δb ) = X0 . Δa ( 1 + Δb )a0 a0 b0 a0 b0
ΔXb = X0 ( ΔXb + ΔXa ΔXb) = X0 (Δb + Δa Δb ) = X0 . Δb ( 1 + Δa )
b0 a0 b0 b0 a0
přednosti: použitelnost při záporných hodnotách indexů, není citlivá na pořadí ukazatelů
nedostatky: relativní přesnost
Слайд 25 PŘ: Aplikujte vliv změn dílčích ukazatelů (rentabilita celkového
kapitálu, celkový kapitál) na ukazatel vrcholový (zisk): a) metodou rozkladu
s postupnými změnami b) metodou rozkladu se zbytkem c) metodou logaritmickou d) metodou funkcionální
Слайд 26
PŘ: výsledky
ad a) metoda rozkladu s postupnými změnami
20
752 = - 278,49 + 21 030,43
ad b) metoda
rozkladu se zbytkem20 752 = -278,49 + 24 053,20 - 3 022,77
ad b) metoda logaritmická
vliv Δ Z/∑K = 21 943,7 vliv Δ ∑K = - 1 191,8
ad c) metoda funkcionální
ΔZZ/∑K = 22 541,43 ΔZ∑K = - 1 789,84
Слайд 27
Du Pontův rozklad – nejznámější pyramidová soustava
Čistý zisk/vlastní
kapitál
Čistý zisk/aktiva
Aktiva/vlastní kapitál
Zisk/tržby
Tržby/aktiva
Čistý zisk
tržby
Čisté tržby
aktiva
tržby
∑N
OA
dl. M
Слайд 29
Analýza soustav ukazatelů →
Ploché soustavy ukazatelů
BONITNÍ
A BANKROTNÍ MODELY
ukazatele jsou účelově vybírány
cílem je sestavit takové
výběry ukazatelů, které by dokázaly kvalitně předpovědět finanční situaci podnikudle jejich tvorby se člení na jednorozměrné a vícerozměrné modely
Слайд 30
BONITNÍ MODELY
diagnostické
hodnotí podnik jedním syntetickým koeficientem, který umožňuje
vyjádřit bonitu firmy
analýza ex post
princip tvorby: 1. výběr ukazatelů
2. ohodnocení
ukazatelů3. součet bodů
4. zařazení firmy do skupiny úspěšnosti
- PŘ: zahraniční – Kralicekův „Rychlý test“, Tamariho model
ČR – Index bonity (IB index)
Слайд 31
Kralicekův „Rychlý test“
navržen v r. 1990
rychlost a poměrně
dobrá vypovídací schopnost
pracuje s následujícími ukazateli:
koeficient samofinancování = vl.
K/∑Adoba splácení dluhu z CF = (ci. K – kr. fin. majetek)/bilanční CF
cash flow v % tržeb = CF/tržby
ROA = HV po zdanění + úroky (1 – daňová sazba) /∑A
každý vypočtený ukazatel se poté oklasifikuje známkami dle tabulky
výsledná známka se pak určí jako jednoduchý aritmetický průměr známek získaných za jednotlivé ukazatele ⇒ < 2: velmi dobrý podnik
> 3: špatná finanční situace
Слайд 33
BANKROTNÍ MODELY
predikční
předpovídají případné ohrožení finančního zdraví podniku
analýza ex
ante
postup sestavování: 1. výběr ukazatelů, které ovlivňují HV nejvíce
2. stanovení
vah ukazatelů3. stanovení funkce vlivu ukazatelů na HV podniku
4. stanovení intervalu hodnot, ve kterém je firma ohrožena bankrotem
- PŘ: Altmanovo „Z-skóre“, Beermanova diskriminační funkce, Taflerův bankrotní model, IN index 95, 99, 01, 05 …….
Слайд 34
Altmanova formule bankrotu (Z-skóre)
vychází z diskriminační analýzy uskutečněné
koncem 60. a v 80. letech u několika desítek
zbankrotovaných a nezbankrotovaných firemZ-skóre pro firmy s veřejně obchodovatelnými akciemi se vypočítá dle vztahu:
Zi = 1,2 . A + 1,4 . B + 3,3 . C + 0,6 . D + 1,0 . E
A = pracovní kapitál /∑A
B = zisk po zdanění/ ∑A
C = zisk před zdaněním a úroky/ ∑A
D = tržní hodnota vlastního kapitálu/celkové dluhy
E = celkové tržby/ ∑A





























