Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Методы решения комбинаторных задач.

Содержание

2. А. Пуанкаре«…творчество, конечно, состоит не в том,
3. Комбинаторика–
4. Способы решения комбинаторных задач: графы; таблицы;дерево решений.
5. Перебор возможных вариантов
6. Задача 1. Какие двузначные числа можно
7. Задача 2. В
8. Задача 3.
9. Дерево возможных вариантов Самые разные комбинаторные задачи
10. Задача 4. Какие трехзначные числа можно
11. Ответ: 200, 202, 204, 220, 222, 224,
12. Задача 5. Школьные туристы решили совершить
13. Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.
14. Задача 6. Запишите все возможные варианты
15. Ответ: Всего 24 возможных варианта:
16. Задача 7. Саша ходит в школу
17. Ответ: а) 16 дней; б) 8 дней; в) 2 дня.
18. Составление таблиц
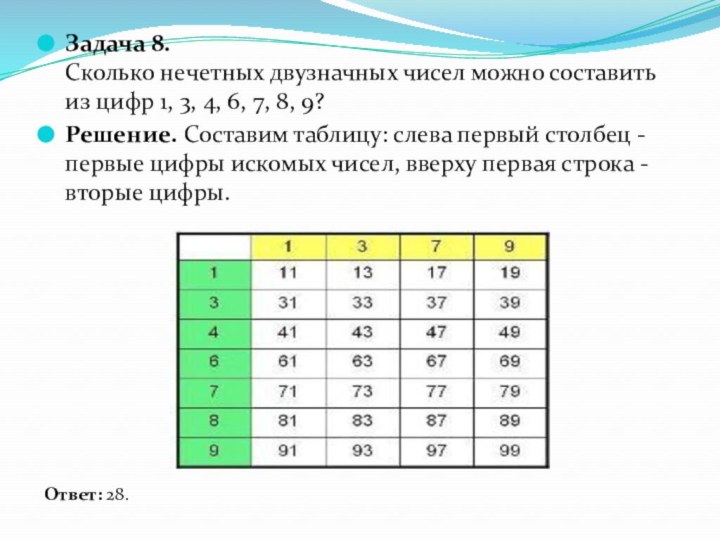
19. Задача 8. Сколько нечетных двузначных чисел
20. Задача 9. Маша, Оля, Вера, Ира,
21. Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.
22. Правило умножения Этот метод решения комбинаторных задач
23. Задача 10. В футбольном турнире участвуют
24. Задача 11. 6 учеников сдают зачет
25. Скачать презентацию
26. Похожие презентации

А. Пуанкаре«…творчество, конечно, состоит не в том, чтобы составлять бесконечные комбинации, а в том, чтобы создавать полезные, а таких не особенно много. Творить – это значит различать, выбирать».

Комбинаторика– это раздел математики, в котором

Способы решения комбинаторных задач: графы; таблицы;дерево решений.

Задача 1. Какие двузначные числа можно составить из цифр 1, 2,

Задача 3. В кружок бального танца записались

Дерево возможных вариантов Самые разные комбинаторные задачи решаются с помощью составления специальных

Задача 4. Какие трехзначные числа можно составить из цифр 0, 2,

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402,

Задача 5. Школьные туристы решили совершить путешествие к горному озеру. Первый

Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

Задача 6. Запишите все возможные варианты расписания пяти уроков на день

Задача 7. Саша ходит в школу в брюках или джинсах, к

Составление таблиц Решить комбинаторные задачи можно с

Задача 8. Сколько нечетных двузначных чисел можно составить из цифр 1,

Задача 9. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились

Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.

Правило умножения Этот метод решения комбинаторных задач применяется, когда не требуется перечислять

Задача 10. В футбольном турнире участвуют несколько команд. Оказалось, что все

Задача 11. 6 учеников сдают зачет по математике. Сколькими способами их

Задача 12. Сколько четных двузначных чисел можно составить из цифр 0,

Слайды презентации

Слайд 2 А. Пуанкаре
«…творчество, конечно, состоит не в том, чтобы

А. Пуанкаре«…творчество, конечно, состоит не в том, чтобы составлять бесконечные комбинации,

составлять бесконечные комбинации, а в том, чтобы создавать полезные,

а таких не особенно много. Творить – это значит различать, выбирать».

Слайд 3 Комбинаторика
– это

Комбинаторика– это раздел математики, в котором исследуются и

раздел математики,
в котором исследуются и
решаются

задачи выбора
элементов из исходного
множества и расположения
их в некоторой комбинации, составляемой по заданным правилам

Слайд 4 Способы решения комбинаторных задач:
графы;
таблицы;
дерево решений.

Слайд 5 Перебор возможных вариантов

Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

Слайд 6 Задача 1. Какие двузначные числа можно составить из

цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13,

14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Слайд 7 Задача 2. В финальном забеге

Задача 2. В финальном забеге на 100 м участвуют

на 100 м участвуют Иванов, Громов и Орлов. Назовите

возможные варианты распределения призовых мест.
Ответ: Вариант1: 1) Иванов, 2) Громов, 3) Орлов. Вариант2: 1) Иванов, 2) Орлов, 3) Громов. Вариант3: 1) Орлов, 2) Иванов, 3) Громов. Вариант4: 1) Орлов, 2) Громов, 3) Иванов. Вариант5: 1) Громов, 2) Орлов, 3) Иванов. Вариант6: 1) Громов, 2) Иванов, 3) Орлов.

Слайд 8 Задача 3. В кружок

Задача 3. В кружок бального танца записались Петя, Коля,

бального танца записались Петя, Коля, Витя, Олег, Таня, Оля,

Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Ответ: 1) Таня - Петя, 2) Таня - Коля, 3) Таня - Витя, 4) Таня - Олег, 5) Оля - Петя, 6) Оля - Коля, 7) Оля - Витя, 8) Оля - Олег, 9) Наташа - Петя, 10) Наташа - Коля, 11) Наташа - Витя, 12) Наташа - Олег, 13) Света - Петя, 14) Света - Коля, 15) Света - Витя, 16) Света - Олег.

Слайд 9 Дерево возможных вариантов
Самые разные комбинаторные задачи решаются

Дерево возможных вариантов Самые разные комбинаторные задачи решаются с помощью составления

с помощью составления специальных схем. Внешне такая схема напоминает

дерево, отсюда и название метода - дерево возможных вариантов.

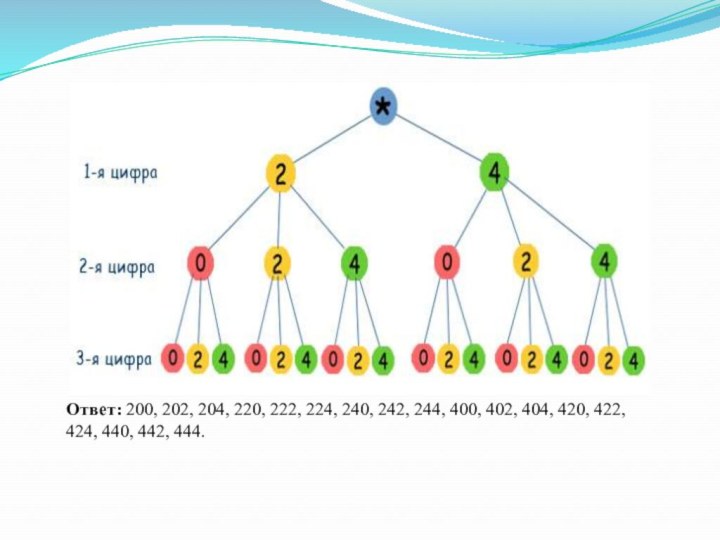
Слайд 10

Задача 4. Какие трехзначные числа можно составить из

цифр 0, 2, 4?

Решение. Построим дерево возможных вариантов, учитывая,

что 0 не может быть первой цифрой в числе.

Слайд 11 Ответ: 200, 202, 204, 220, 222, 224, 240,

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400,

242, 244, 400, 402, 404, 420, 422, 424, 440,

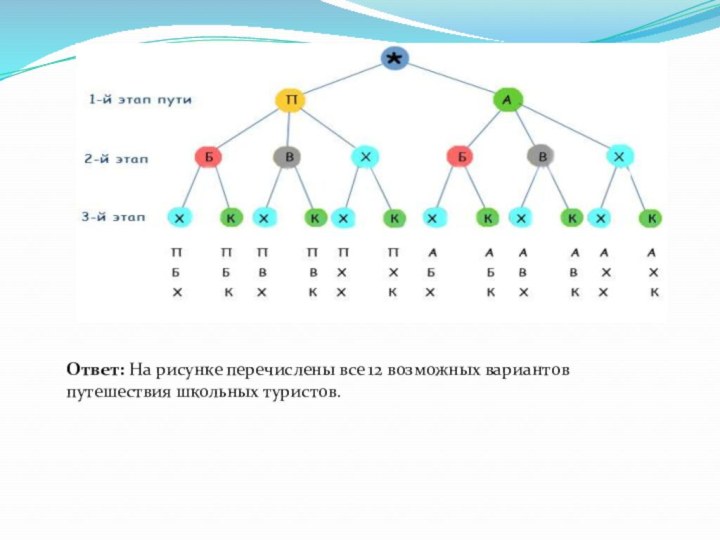
442, 444.

Слайд 12 Задача 5. Школьные туристы решили совершить путешествие к

горному озеру. Первый этап пути можно преодолеть на поезде

или автобусе. Второй этап - на байдарках, велосипедах или пешком. И третий этап пути - пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?
Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе - А, на байдарках - Б, велосипедах - В, пешком - Х, на канатной дороге - К.

Слайд 13 Ответ: На рисунке перечислены все 12 возможных вариантов

путешествия школьных туристов.

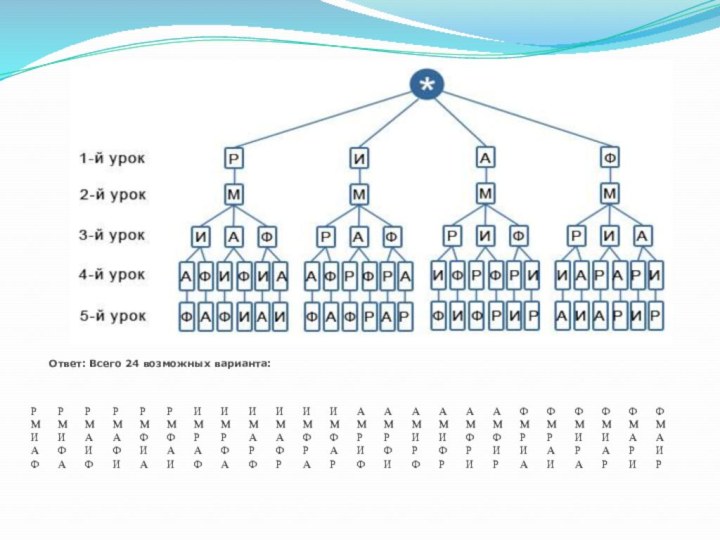
Слайд 14 Задача 6. Запишите все возможные варианты расписания пяти

уроков на день из предметов: математика, русский язык, история,

английский язык, физкультура, причем математика должна быть вторым уроком.
Решение. Построим дерево возможных вариантов, обозначив М - математика, Р - русский язык, И - история, А - английский язык, Ф - физкультура.

Слайд 15

Ответ: Всего 24 возможных варианта:

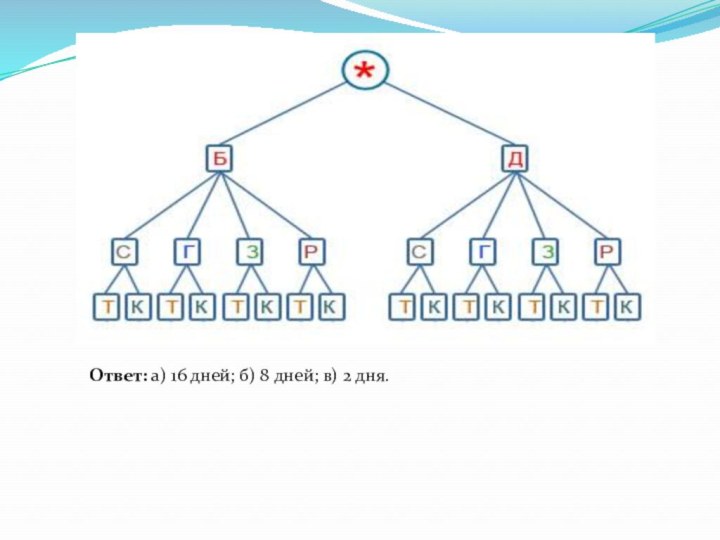
Слайд 16 Задача 7. Саша ходит в школу в брюках

или джинсах, к ним одевает рубашки серого, голубого, зеленого

цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки. а) Сколько дней Саша сможет выглядеть по-новому? б) Сколько дней при этом он будет ходить в кроссовках? в) Сколько дней он будет ходить в рубашке в клетку и джинсах?
Решение. Построим дерево возможных вариантов, обозначив Б - брюки, Д - джинсы, С - серая рубашка, Г - голубая рубашка, З - зеленая рубашка, Р - рубашка в клетку, Т - туфли, К - кроссовки.

Слайд 17 Ответ: а) 16 дней; б) 8 дней; в)

2 дня.

Слайд 18 Составление таблиц

Составление таблиц Решить комбинаторные задачи можно с помощью

Решить комбинаторные задачи можно с помощью таблиц. Они, как

и дерево возможных вариантов, наглядно представляют решение таких задач.

Слайд 19 Задача 8. Сколько нечетных двузначных чисел можно составить

из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец - первые цифры искомых чисел, вверху первая строка - вторые цифры.

Ответ: 28.

Слайд 20 Задача 9. Маша, Оля, Вера, Ира, Андрей, Миша

и Игорь готовились стать ведущими на Новогоднем празднике. Назовите

возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.

Слайд 21 Ответ: Все возможные варианты перечисляются в строках и

столбцах таблицы.

Слайд 22 Правило умножения

Этот метод решения комбинаторных задач применяется,

Правило умножения Этот метод решения комбинаторных задач применяется, когда не требуется

когда не требуется перечислять все возможные варианты, а нужно

ответить на вопрос - сколько их существует.

Слайд 23 Задача 10. В футбольном турнире участвуют несколько команд.

Оказалось, что все они для трусов и футболок использовали

белый, красный, синий и зеленый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире?
Решение. Трусы могут быть белого, красного, синего или зеленого цвета, т.е. существует 4 варианта. Каждый из этих вариантов имеет 4 варианта цвета майки.
4 х 4 = 16.
Ответ: 16 команд.

Слайд 24 Задача 11. 6 учеников сдают зачет по математике.

Сколькими способами их можно расположить в списке?
Решение. Первым в

списке может оказаться любой из 6 учеников, вторым в списке может быть любой из оставшихся 5 учеников, третьим - любой из оставшихся 4 учеников, четвертым - любой из оставшихся 3 учеников, пятым - любой из оставшихся 2 учеников, шестым - последний 1 ученик.
6 х 5 х 4 х 3 х 2 х 1 = 720.
Ответ: 720 способами.