Слайд 2
Принципы формирования П(Ĩ)
М(ĩ) СА(Ф) ĩ участвует
в ŊĨ (Ф) Ý(ĩ)
Ý зависит от успехов Ф
= эффективности ŘĨ
min y'о, соответствующий ожиданиям ĩ
Слайд 3
Факторы ожидания ĩ
ĩ: a ρ; в
надежде на y' = 20%
предложение ḿ: y'(Ŋ)
20%
20% играют роль норматива ŘĨ
Почему ĩ ожидает 20% (40% ; 5%) ?
CAPM:
ρ(a) + p(ρ) на μ в % y'(ожидаемой)
Слайд 4
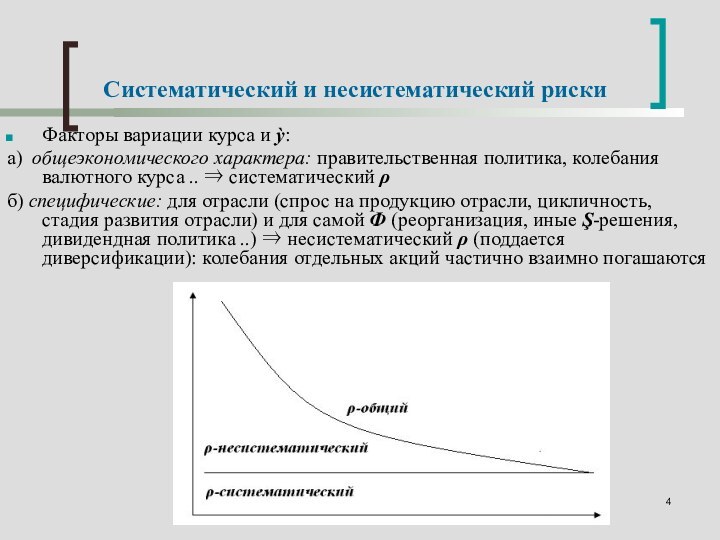
Систематический и несистематический риски
Факторы вариации курса и ỳ:
а)
общеэкономического характера: правительственная политика, колебания валютного курса ..
систематический ρ
б) специфические: для отрасли (спрос на продукцию отрасли, цикличность, стадия развития отрасли) и для самой Ф (реорганизация, иные Ş-решения, дивидендная политика ..) несистематический ρ (поддается диверсификации): колебания отдельных акций частично взаимно погашаются
Слайд 5
Систематический и несистематический риски
ρ: y' < y'о
ρ
: неопределенность Ĩ = изменчивость (вариация, колеблемость)
курса и y'(а).
вариация y' = мера ρĨ
(с определенной долей условности)
Слайд 6
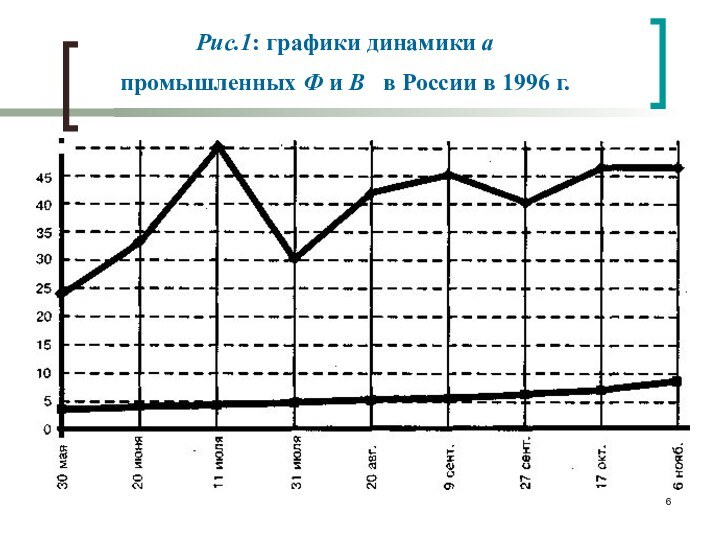
Рис.1: графики динамики а
промышленных Ф и В
в России в 1996 г.
Слайд 7
Диверсификация
П : различные ценные бумаги суммарная
вариация их курса и y'
диверсификация: ρ при
формировании П
динамика П более стабильна, чем отдельных активов
Слайд 8
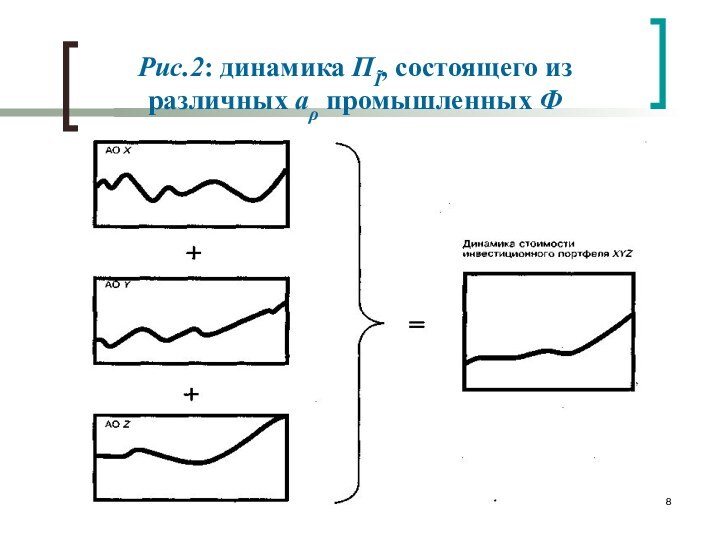
Рис.2: динамика ПĨ, состоящего из различных аρ промышленных
Слайд 9
Причины вариации курса и ỳ ценных бумаг
а) факторы
общеэкономического характера, влияющие на фондовый μ в целом (,
колебания валютного курса и др.);
б) факторы специфические:
для отрасли, в которой работает Ф;
для самой Ф или осуществляемого ею проекта (аварии, принятие решений о реорганизации и т.п.).
Слайд 10
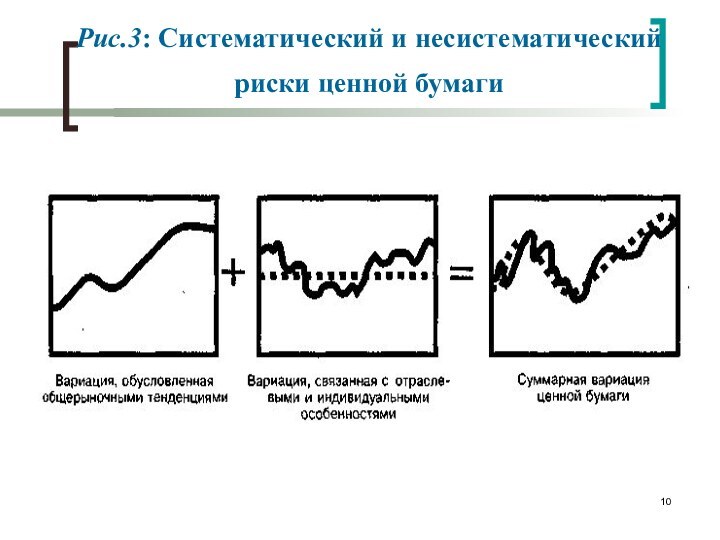
Рис.3: Систематический и несистематический риски ценной бумаги
Слайд 11
Риски
Систематический ρ = изменчивость ценных бумаг, обусловленная общеэкономическими
колебаниями, т.е. изменениями μ в целом.
Этот ρ не
поддается диверсификации недиверсифицируемый.
Несистематический ρ = вариация курса и ỳ ценных бумаг, обусловленная отраслевыми и индивидуальными особенностями эмитента.
Этот ρ поддается диверсификации.
Хорошо диверсифицированный ПĨ = несистематический ρ пренебрежимо мал
Слайд 12
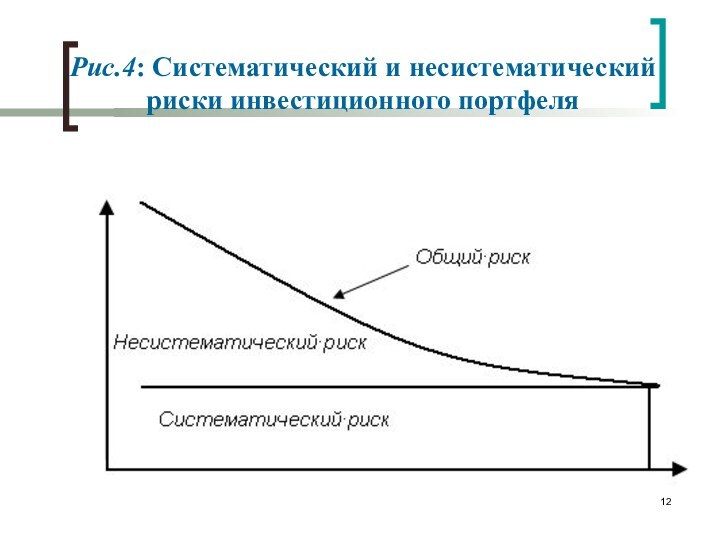
Рис.4: Систематический и несистематический
риски инвестиционного портфеля
Слайд 13
Измерение систематического риска. Бета-фактор
Различные
ценные бумаги по-разному реагируют на общеэкономические колебания: одни более
устойчивы по отношению к тенденциям μ, чем другие.
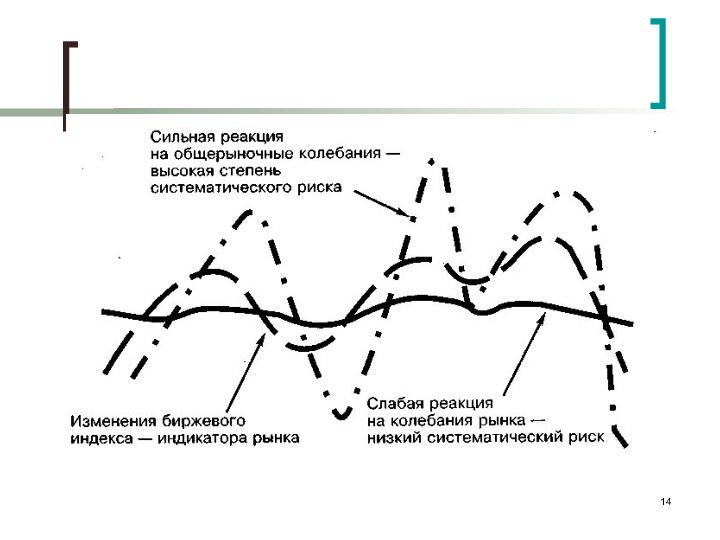
Рис.5: Систематический ρ для каждой отдельной ценной бумаги отличается от систематического ρ, среднего для μ в целом.
Слайд 15
Бета-фактор
Степень систематического ρ оценивается параметром (коэффициентом) = «бета-фактор»:
μ
в целом: = 1;
безрисковое вложение: = 0;
ценная
бумага с коэффициентом < 1 имеет меньший систематический ρ, чем μ в целом
ценная бумага с коэффициентом > 1 имеет больший систематический ρ, чем средний ρ по μ
Слайд 16
Как определить коэффициент ?
Для ценных бумаг Ф, имеющих
котировку на μ, коэффициент систематического ρ часто рассчитывается централизованно.
Расчет: сопоставление динамики биржевого индекса (μ в целом) и динамики конкретной а, по которой рассчитывается .
оценивается как коэффициент регрессии в уравнении парной корреляционной связи вида:
у = а + х + е
у - ỳ конкретной а, х - среднерыночная ỳ, е - случайная величина
Если по а на данном μ не выплачиваются дивиденды, темп прироста курса акции и темп прироста биржевого индекса соответственно будут равны ỳ акции (у) и ỳ по μ в среднем (х).
Слайд 17
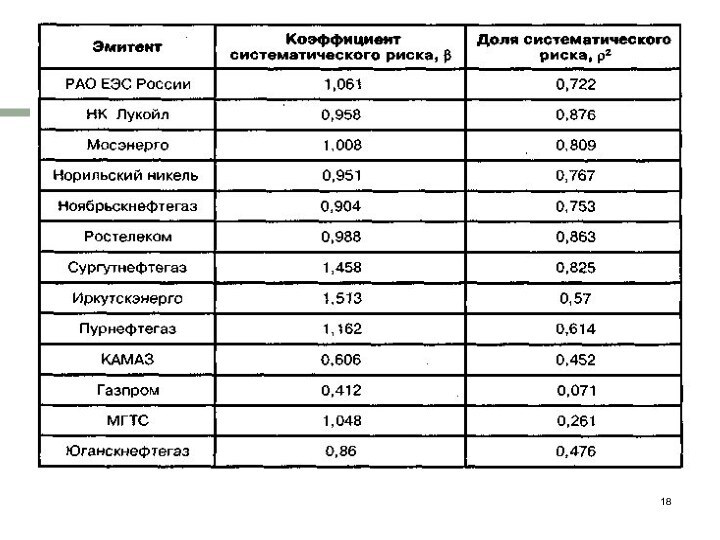
Таблица
значения коэффициентов систематического ρ, рассчитанные по некоторым ведущим
российским Ф в 1996-1997 гг.
Там же представлены коэффициенты
ρ2 (квадрат коэффициента корреляции), показывающие, какая часть общей вариации конкретной а объясняется колебаниями μ, т.е. какая часть общего ρ имеет систематическую природу.
Слайд 19
САРМ
для оценки y'(П) для Ĭ, который способен с
помощью диверсификации избавиться от несистематического ρ и который предполагает
получить определенный уровень y' за принятый систематический ρ.
дает возможность оценить ставку дисконта, Ĭ-проекта, базируясь на его систематическом ρ.
Слайд 20
САРМ исходит из ряда допущений, не вполне согласующихся
с реальной практикой
предполагается, что Ĭ владеют хорошо диверсифицированными П
(не принимаются во внимание несистематический ρ);
САРМ является равновесной моделью для совершенного μС и игнорирует налогообложение, разницу в доступности ĭ, трансакционные издержки, различия ставок по К и депозитам; все Ĭ на μ мыслят сходным образом и измеряют время в одних единицах;
среднерыночная y' = y' биржевого индекса, а y' долгосрочных дисконтных государственных ценных бумаг является безрисковой.
Слайд 21
Как зависит требуемый уровень ỳ
на вложенный С
от систематического ρ?
Если Ĭ является безрисковой, то соответствующий
ей = 0 (отсутствие ρ),
ставка требуемой y' = безрисковая ставка Rf.
Если Ĭ имеет такой же ρ, как и μ в среднем, то = 1, ставка требуемой y' = ожидаемая y' по μ в целом.
На практике такая y', обозначаемая Rm = ожидаемая ỳ биржевого индекса, характеризующего μ.
Зависимость требуемого уровня y' от систематического ρ линейная:
ρ (т.е. -фактор) требования к y' (Е(r)).
Слайд 22
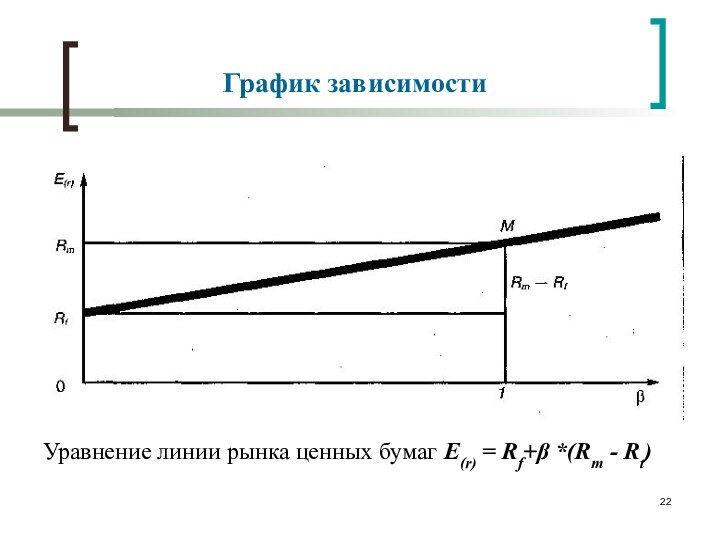
График зависимости
Уравнение линии рынка ценных бумаг E(r) =
Rf+ *(Rm - Rt)