- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория игр – как метод экономического анализа
Содержание
- 2. Теория игр - математический метод изучения оптимальных стратегий
- 3. Основные понятия Игра – ситуация, участники которой принимают
- 4. Представление игр Игры представляют собой строго определённые математические
- 5. Представление игр Игры в экстенсивной, или расширенной, форме
- 6. Представление игр В нормальной, или стратегической, форме игра
- 7. Представление игр Кооперативные игры используют так называемую характеристическую
- 8. Типы игр – Кооперативные и некооперативные; – Симметричные и несимметричные; – С нулевой
- 9. Дилемма заключённых
- 10. Примеры игр Рассмотрим двух гигантов, конкурирующих на рынке
- 11. В случае, если «Боинг» и «Эйрбас» договариваются
- 12. Прибыль участников будет максимальна, если они оба
- 13. Долларовый аукцион Сущность игры заключается в следующем. Проводится
- 14. Применение теории игр в экономике Тривиальным с позиций
- 15. Скачать презентацию
- 16. Похожие презентации
Теория игр - математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию,











Слайд 2 Теория игр - математический метод изучения оптимальных стратегий в
играх.
и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу - в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.
Слайд 3
Основные понятия
Игра – ситуация, участники которой принимают решения
в условиях взаимозависимости.
Игрок - участник, принимающий решения. Стратегия
- план действий игрока в условиях взаимозависимости. Выигрыш игрока – результат реализации стратегии. Игра – ситуация, участники которой принимают решения в условиях взаимозависимости.
Платежная матрица игры – один из способов представления игры, таблица, в которой отражаются выигрыши (платежи) игроков при выборе ими различных стратегий. Равновесие в игре - набор стратегий, в наибольшей степени устраивающих всех участников. Доминантная стратегия – стратегия, предпочтительная для одного игрока вне зависимости от стратегии, выбранной другим игроком.
Слайд 4
Представление игр
Игры представляют собой строго определённые математические объекты.
Игра образуется игроками, набором стратегий для каждого игрока и
указания выигрышей, или платежей, игроков для каждой комбинации стратегий. Большинство кооперативных игр описываются характеристической функцией, в то время как для остальных видов чаще используют нормальную или экстенсивную форму.
Слайд 5
Представление игр
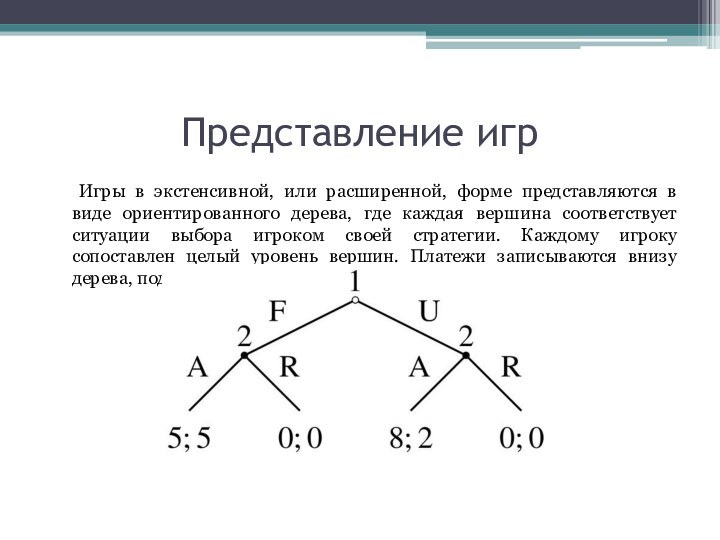
Игры в экстенсивной, или расширенной, форме представляются
в виде ориентированного дерева, где каждая вершина соответствует ситуации
выбора игроком своей стратегии. Каждому игроку сопоставлен целый уровень вершин. Платежи записываются внизу дерева, под каждой листовой вершиной.
Слайд 6
Представление игр
В нормальной, или стратегической, форме игра описывается
платёжной матрицей. Каждая сторона (точнее, измерение) матрицы это игрок,
строки определяют стратегии первого игрока, а столбцы второго. На пересечении двух стратегий можно увидеть выигрыши, которые получат игроки.Если игрок 1 выбирает Ai , а игрок 2 – Bj , то выигрыши игроков 1 и 2 равны соответственно aij и bij (i = 1, .., m; j = 1, .., n).
Слайд 7
Представление игр
Кооперативные игры используют так называемую характеристическую функцию,
определяющую выигрыш каждой коалиции игроков. При этом предполагается, что
выигрыш пустой коалиции равен нулю.Если в игре с двумя сторонами образуется коалиция C, то против неё выступает коалиция N\C. Образуется как бы игра для двух игроков. Но так как вариантов возможных коалиций много (а именно 2N, где N — количество игроков), то выигрыш для C будет некоторой характеристической величиной, зависящей от состава коалиции. Формально игра в такой форме (также называемая TU-игрой) представляется парой (N, v), где N — множество всех игроков, а v: 2N → R — это характеристическая функция.
Слайд 8
Типы игр
– Кооперативные и некооперативные;
– Симметричные и несимметричные;
– С нулевой суммой
и с ненулевой суммой;
– Параллельные и последовательные;
– С полной или неполной информацией;
– Игры
с бесконечным числом шагов;– Дискретные и непрерывные игры;
– Метаигры.
Слайд 10
Примеры игр
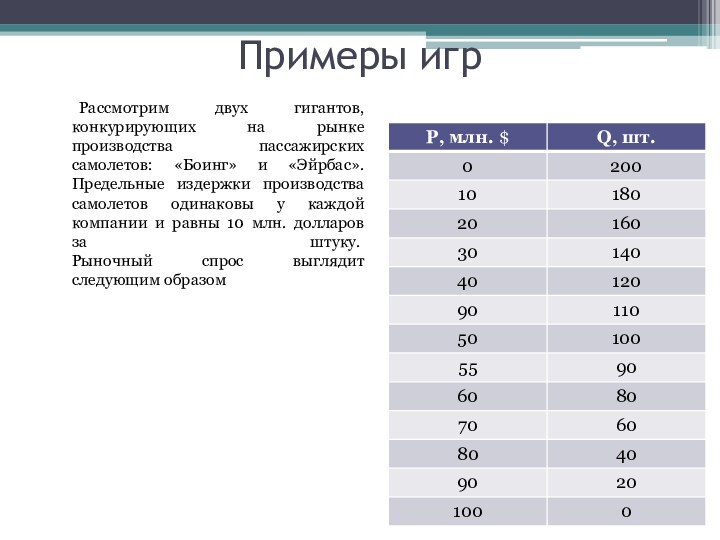
Рассмотрим двух гигантов, конкурирующих на рынке производства
пассажирских самолетов: «Боинг» и «Эйрбас». Предельные издержки производства самолетов
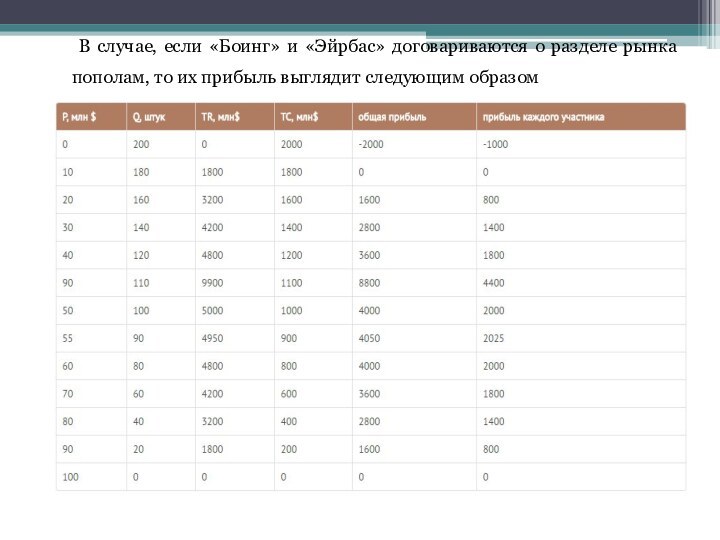
одинаковы у каждой компании и равны 10 млн. долларов за штуку. Рыночный спрос выглядит следующим образомСлайд 11 В случае, если «Боинг» и «Эйрбас» договариваются о
разделе рынка пополам, то их прибыль выглядит следующим образом
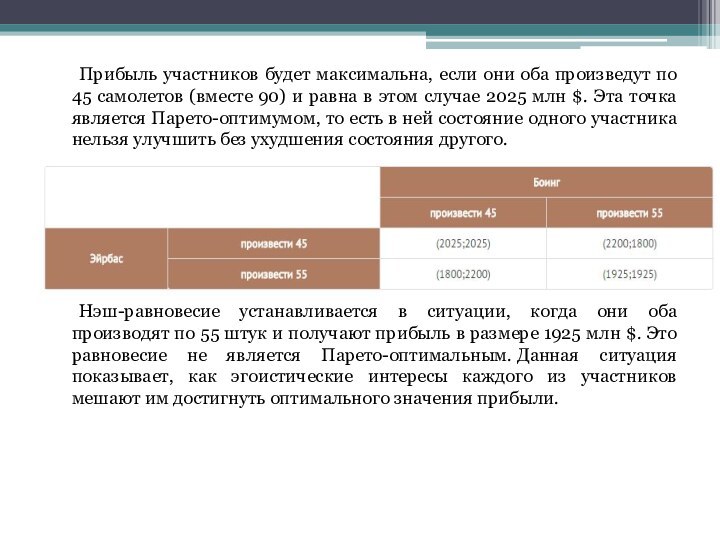
Слайд 12 Прибыль участников будет максимальна, если они оба произведут
по 45 самолетов (вместе 90) и равна в этом
случае 2025 млн $. Эта точка является Парето-оптимумом, то есть в ней состояние одного участника нельзя улучшить без ухудшения состояния другого.Нэш-равновесие устанавливается в ситуации, когда они оба производят по 55 штук и получают прибыль в размере 1925 млн $. Это равновесие не является Парето-оптимальным. Данная ситуация показывает, как эгоистические интересы каждого из участников мешают им достигнуть оптимального значения прибыли.





























