- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория поведения потребителей
Содержание
- 2. Рыночный спрос формируется на основе решений, принимаемых
- 3. Термин «полезность» был введен английским философом И.
- 4. Утилитаризм – (от лат. utilitas – польза,
- 5. 3.1. Количественный (кардиналистский) подход к анализу полезности и спроса
- 6. Кардиналистская (количественная) полезность – субъективная полезность, или
- 7. Кардиналистскую (количественную) теорию предельной полезности предложили независимо
- 8. Количественный подход к анализу полезности предполагает возможность:
- 9. Формально это можно записать в виде функции
- 10. Существует множество уравнений, описывающих данную функцию, но
- 11. Изменение TU товарного набора в зависимости от
- 12. Предельная полезность – это прирост совокупной полезности
- 13. Геометрически (нижняя часть рисунка) значение предельной полезности
- 14. Принцип убывания предельной полезности или первый закон
- 15. Математически это означает, что первая производная функции
- 16. Предположим, что потребитель располагает некоторым доходом; цены
- 17. 1) для всех реально покупаемых им товаров
- 18. MUA/PA – прирост общей полезности в результате
- 19. 2) для всех непокупаемых им товаров Y,
- 20. Основное условие потребительского оптимума или Второй закон
- 21. 3.2. Аксиомы порядкового (ординалистского подхода) к анализу полезности и спроса.
- 22. Порядковый подход к анализу полезности и спроса:1.
- 23. При порядковом подходе используются кривые и карта безразличия.
- 24. Кривая безразличия – это множество точек, каждая
- 25. Если заполнить двухмерную плоскость кривыми безразличия так
- 26. Вектор смещения кривых безразличия в сторону все более полного удовлетворения называется «вектором счастья».
- 27. Карта безразличия
- 28. Товарный набор А включает ХА единиц товара
- 29. Порядковый подход базируется на следующих аксиомах:
- 30. 1. Аксиома полной (совершенной) упорядоченности, или сравнимости
- 31. Три варианта: 1) либо набор А предпочтительнее
- 32. 2. Аксиома транзитивности Если для любых трех
- 33. Аксиома полной упорядоченности и аксиома транзитивности позволяют считать, что предпочтения согласованны и рациональны.
- 34. 3. Аксиома рефлексивностиДанная аксиома предполагает, что любой
- 35. Эти аксиомы позволяют понять, что каждый набор
- 36. 4. Аксиома ненасыщения Предполагает отсутствие у потребителя
- 37. 5. Аксиома непрерывности Любой товар может быть
- 38. 6. Аксиома строгой выпуклости к началу
- 40. Соблюдение вышеперечисленных предпосылок позволяет графически изобразить предпочтения
- 41. Свойства кривых безразличия
- 42. 1. Кривая безразличия, лежащая выше и правее
- 43. Набор С содержит такое же количество товара
- 44. 2. Кривые безразличия имеют отрицательный наклон.Пусть дана
- 45. Очевидно, что все точки, лежащие в III
- 46. 3. Кривые безразличия никогда не пересекаются. Предположим
- 47. Из аксиомы о ненасыщении следует, что А
- 48. 4. Кривая безразличия может быть проведена через
- 49. 5. Кривые безразличия выпуклы к началу координат.
- 50. Основным рабочим понятием порядковой теории полезности является
- 51. Норма, в которой человек готов заменить одно
- 52. Виды кривых безразличия:
- 53.
- 54.
- 56. Предпочтения нормального вида являются гомотетичными (подобными), т.е.
- 57. 2. Кривые безразличия для взаимозаменяемых товаров
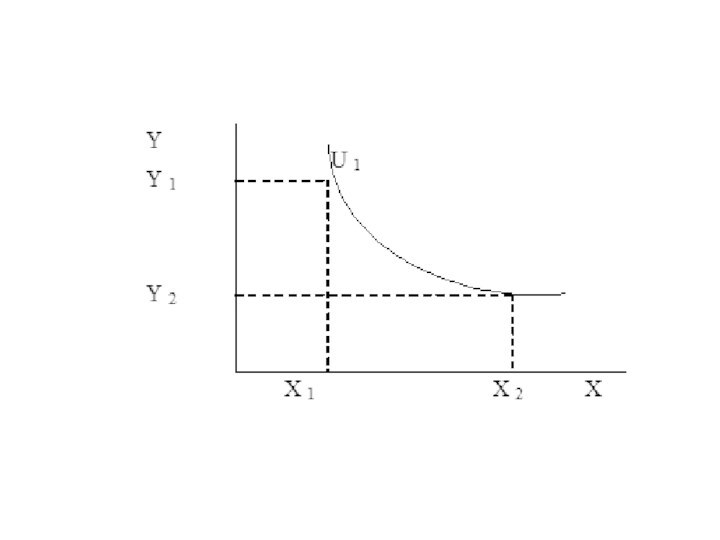
- 59. 3. Кривые безразличия для взаимодополняемых благ (совершенных
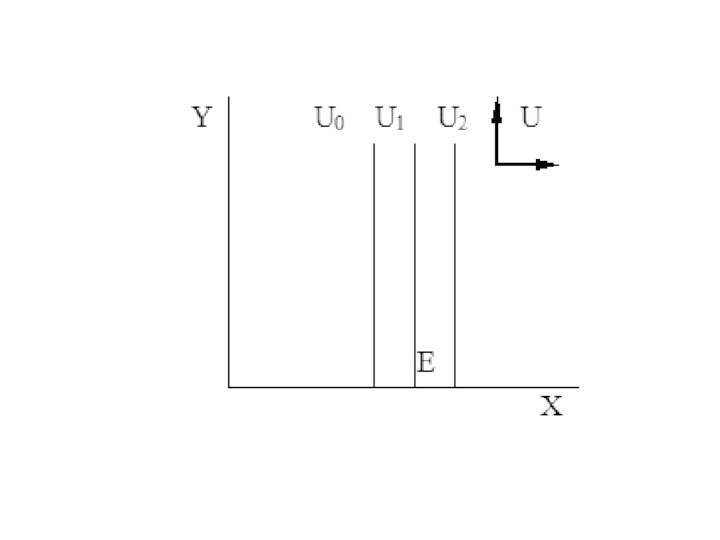
- 61. 4. Кривые безразличия для независимых (нейтральных, безразличных)
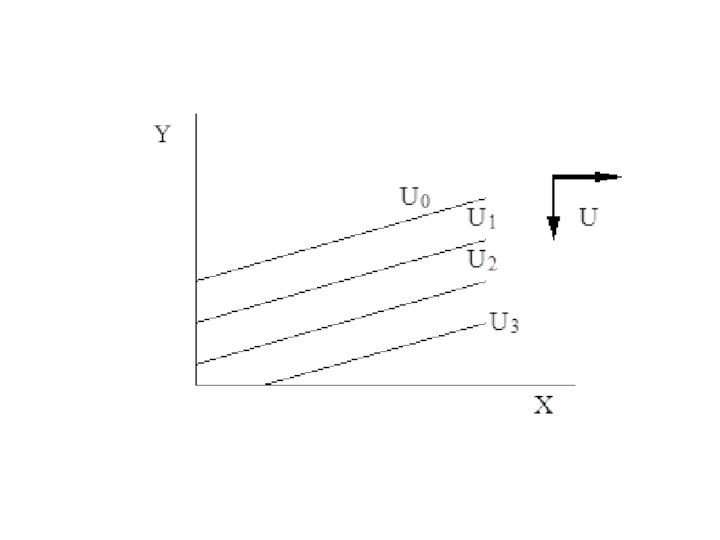
- 63. 5. Благо и антиблаго или товары, нежелательные
- 64. Функцию полезности для набора (X,Y) с благом
- 66. 6. Несовместимые товары – эти товары лучше
- 68. 7. Квазилинейные предпочтения – это такой
- 69. Функцию полезности для набора (X,Y) можно представить
- 71. 8. Лексикографические предпочтения когда все потребительские наборы
- 73. Пусть потребительский набор состоит из двух
- 74. 9. Дискретные (неделимые) благаДанный товар можно приобретать
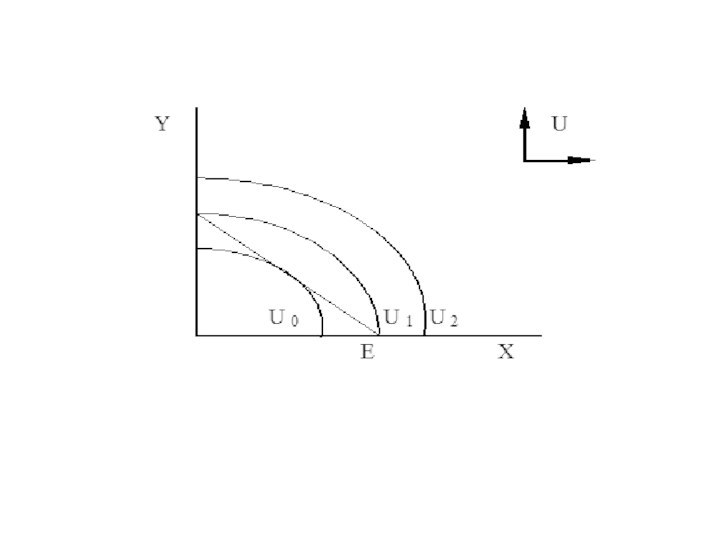
- 76. 10. Набор с точкой насыщенияСитуация, при которой
- 78. Функцию полезности для набора (X.Y) можно представить
- 79. Скачать презентацию
- 80. Похожие презентации
Рыночный спрос формируется на основе решений, принимаемых множеством отдельных лиц, которые руководствуются своими платежеспособными потребностями. Но для того чтобы распределить свои средства между разнообразными потребностями, необходимо иметь какую-то общую основу для их сопоставления.































































Слайд 2 Рыночный спрос формируется на основе решений, принимаемых множеством
отдельных лиц, которые руководствуются своими платежеспособными потребностями.
того чтобы распределить свои средства между разнообразными потребностями, необходимо иметь какую-то общую основу для их сопоставления.
Слайд 3
Термин «полезность» был введен английским философом И. Бентамом.
Иеремия
(Джереми) Бентам 15.02.1748 – 6.06.1832) – английский социолог, юрист,
один из крупнейших теоретиков политического либерализма, родоначальник одного из направлений в английской философии – утилитаризма.Слайд 4 Утилитаризм – (от лат. utilitas – польза, выгода)
– направление в этике (этическая теория), согласно которому моральная
ценность поведения или поступка определяется его полезностью.На этом основании была создана теория потребительского поведения, основанная на гипотезе о сопоставимости полезности разнообразных благ.
Известны два основных подхода к анализу полезности – количественный и порядковый.
Слайд 6 Кардиналистская (количественная) полезность – субъективная полезность, или удовлетворение,
которые потребитель получает от потребления благ, измеренные в абсолютных
величинах.Следовательно, можно измерить точную величину полезности, которую потребитель извлекает из потребления блага.
Слайд 7 Кардиналистскую (количественную) теорию предельной полезности предложили независимо друг
от друга У. Джевонс (1835-1882), К. Менгер (1840-1921) и
Л. Вальрас (1834-1910) в последней трети XIX в. Эту теорию разделял А. Маршалл.
Слайд 8
Количественный подход к анализу полезности предполагает возможность:
1.
Измерения различных благ в гипотетических единицах полезности – ютилах
(от англ. utility – полезность).2. Количественной оценки в ютилах полезности любого потребляемого им товарного набора
Не предполагает возможность:
1. Объективного измерения полезности того или иного товара в ютилах
2. Соизмерения объемов удовлетворения, получаемых различными потребителями.
Слайд 9 Формально это можно записать в виде функции совокупной
(общей) полезности:
TU = F(QA,QB,..,QZ),
где ТU – совокупная (общая)
полезность данного товарного набора; QA,QB, …,QZ – объемы потребления товаров А, В, ..., Z в единицу времени.
Слайд 10 Существует множество уравнений, описывающих данную функцию, но наиболее
часто применяемым является:
TU = а + bq + cq²
– dq³,где q – количество потребленного товара;
a, b, c, d – положительные константы.
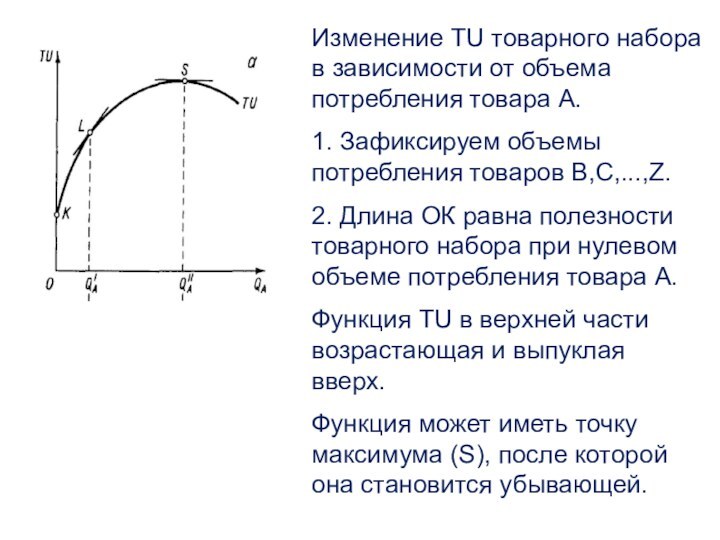
Слайд 11 Изменение TU товарного набора в зависимости от объема
потребления товара А.
1. Зафиксируем объемы потребления товаров B,C,...,Z.
2. Длина ОК равна полезности товарного набора при нулевом объеме потребления товара А.
Функция TU в верхней части возрастающая и выпуклая вверх.
Функция может иметь точку максимума (S), после которой она становится убывающей.
Слайд 12 Предельная полезность – это прирост совокупной полезности товарного
набора при увеличении объема потребления данного товара на одну
единицу.Математически предельная полезность товара есть частная производная совокупной полезности товарного набора по объему потребления i-того товара:
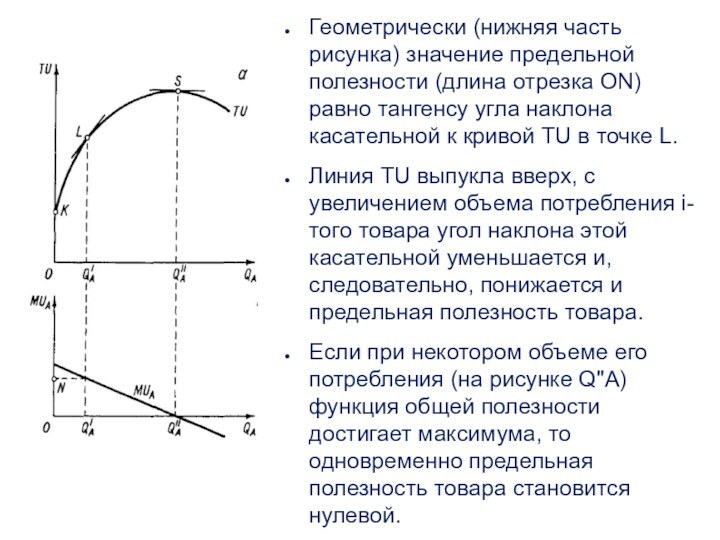
Слайд 13 Геометрически (нижняя часть рисунка) значение предельной полезности (длина
отрезка ON) равно тангенсу угла наклона касательной к кривой
TU в точке L.Линия TU выпукла вверх, с увеличением объема потребления i-того товара угол наклона этой касательной уменьшается и, следовательно, понижается и предельная полезность товара.
Если при некотором объеме его потребления (на рисунке Q"A) функция общей полезности достигает максимума, то одновременно предельная полезность товара становится нулевой.
Слайд 14 Принцип убывания предельной полезности или первый закон Госсена
(немецкий экономист Г. Госсена (1810-1859), впервые сформулировал его в
1854г.):с ростом потребления какого-то одного блага (при неизменном объеме потребления всех остальных) совокупная полезность, получаемая потребителем, возрастает, но возрастает все более медленно, а дополнительная полезность от потребления одного дополнительного блага уменьшается по мере того, как возрастает объем потребления данного блага.
Слайд 15 Математически это означает, что первая производная функции совокупной
полезности по количеству данного блага положительна, а вторая –
отрицательна:Слайд 16 Предположим, что потребитель располагает некоторым доходом; цены на
товары А, В,..., Z не зависят от его поведения
и равны соответственно PA, PB,…, PZ; товарного дефицита нет; все товары являются бесконечно делимыми.При этом потребитель достигнет максимума удовлетворения, если он распределит свои средства на покупку различных товаров таким образом, что:
Слайд 17 1) для всех реально покупаемых им товаров А,
В, С,... имеет место:
где MUA,MUB,MUC – предельные полезности
товаров А,В,С;λ – некоторая величина, характеризующая предельную полезность денег.
Слайд 18 MUA/PA – прирост общей полезности в результате увеличения
расходов потребителя на товар А на 1 денежную единицу.
В
оптимуме (максимум полезности при данных вкусах потребителя, ценах и доходах) полезность, извлекаемая из последней денежной единицы, потраченной на покупку какого-либо товара, одинакова, независимо от того, на какой именно товар она израсходована.Слайд 19 2) для всех непокупаемых им товаров Y, Z,...
имеет место
Если уже 1-ая у.е., израсходованная на покупку
товара Z, приносит потребителю недостаточно высокую полезность, то он вообще отказывается от потребления этого товара.
Слайд 20
Основное условие потребительского оптимума или Второй закон Госсена
Для
максимизации полезности потребитель должен таким образом распределить свой ограниченный
бюджет, чтобы предельные полезности на один рубль, затраченный на последнюю единицу каждого товара, равнялись бы между собой:MUА/PА=MUВ/PВ=…=MUZ/PZ,
а сумма всех затрат потребителя на товары и услуги плюс сбережения (S) соответствовала его денежному доходу (R), то есть:
PAQA+PBQB+…+PZQZ+S=R.
Если эти предельные полезности не равны, то совокупное удовлетворение может быть увеличено путем уменьшения расходов на товары с меньшей степенью полезности и увеличения затрат на товары с большей степенью полезности.
Слайд 22
Порядковый подход к анализу полезности и спроса:
1. Более
современный.
2. Основывается на менее жестких предположениях, чем количественный:
а)
от потребителя не требуется умения измерять полезность того или иного блага в искусственных единицах измерения;б) от потребителя требуется способность упорядочить все возможные товарные наборы по их «предпочтительности».
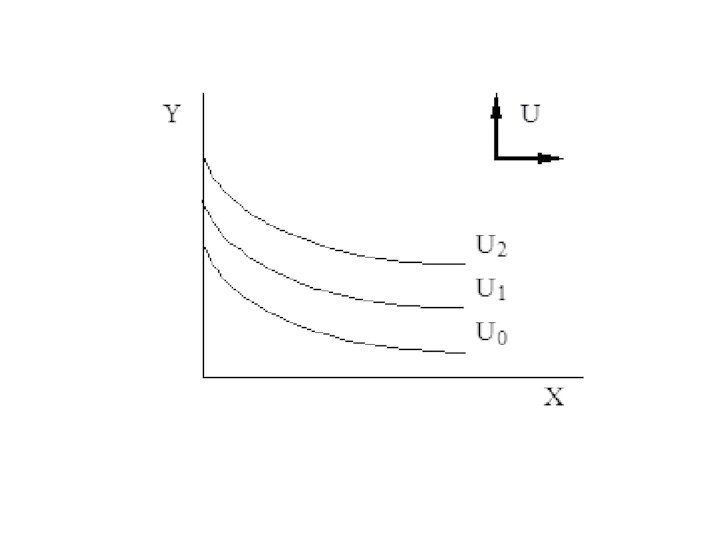
Слайд 24 Кривая безразличия – это множество точек, каждая из
которых представляет собой такой набор из двух товаров, что
потребителю безразлично, какой из этих наборов выбрать.Данные потребительские наборы обеспечивают одинаковый уровень удовлетворения потребностей потребителя (или одинаковую полезность).
Форма кривой безразличия отдельного потребителя определяется его вкусами и предпочтениями и не зависит от доходов или цен на потребляемые товары.
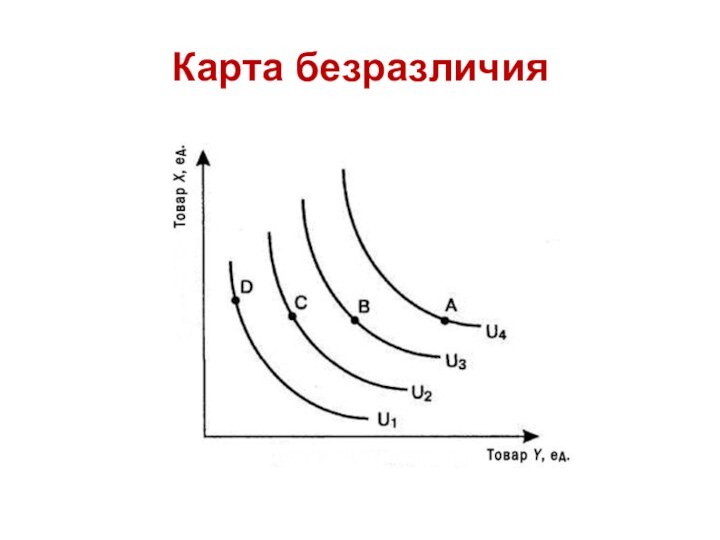
Слайд 25 Если заполнить двухмерную плоскость кривыми безразличия так плотно,
как это возможно, получим карту безразличия.
Карта безразличия – совокупность
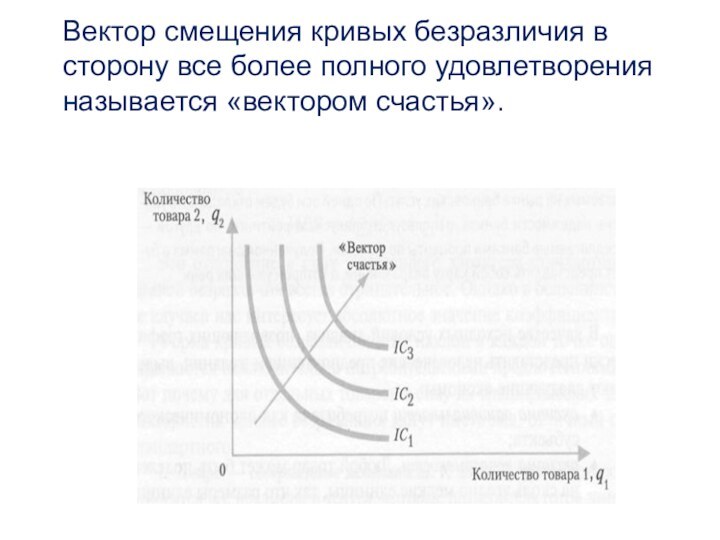
кривых безразличия, описывающих поведение одного потребителя.Слайд 26 Вектор смещения кривых безразличия в сторону все более
полного удовлетворения называется «вектором счастья».
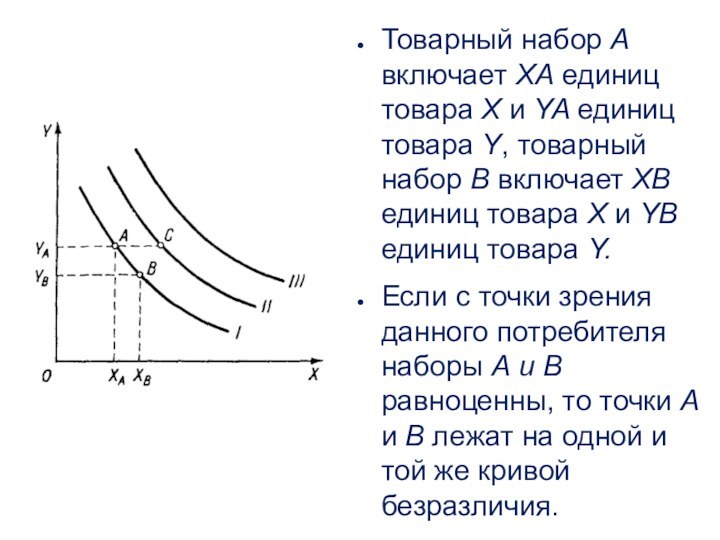
Слайд 28 Товарный набор А включает ХА единиц товара X
и YA единиц товара Y, товарный набор В включает
ХB единиц товара X и YB единиц товара Y.Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной и той же кривой безразличия.
Слайд 30 1. Аксиома полной (совершенной) упорядоченности, или сравнимости (аксиома
возможности выбора)
Выявляет предпочтительность потребительских наборов –
А или
В.
Слайд 31
Три варианта:
1) либо набор А предпочтительнее набора
В (А>В),
2) либо набор В предпочтительнее набора А
(В>А), 3) либо наборы А и В имеют одинаковую полезность для потребителя (А~В).
Следовательно, если А>В, то невозможна ситуация, когда В>А.
Слайд 32
2. Аксиома транзитивности
Если для любых трех потребительских
наборов А, В и С: А > В >
С, А ~ В > С, или А > В ~ С, то А > С.Аксиома гарантирует согласованность предпочтений и исключает возможность следующей ситуации: А > В, В > С и одновременно С > А.
Аксиома содержит утверждение: если А ~ В и В ~ С, то А ~ С.
Слайд 33 Аксиома полной упорядоченности и аксиома транзитивности позволяют считать,
что предпочтения согласованны и рациональны.
Слайд 34
3. Аксиома рефлексивности
Данная аксиома предполагает, что любой набор
благ не хуже себя самого (А~А).
В соответствии с
этой аксиомой каждый набор благ принадлежит хотя бы одной кривой безразличия, а именно, той, которая содержит этот набор.Слайд 35 Эти аксиомы позволяют понять, что каждый набор (аксиома
1) находится на одной кривой безразличия (аксиома 3), причем
не более, чем на одной кривой безразличия (аксиома 2). Из этого следует, что кривые безразличия никогда не пересекаются.
Слайд 36
4. Аксиома ненасыщения
Предполагает отсутствие у потребителя в
ближайшей перспективе порога насыщения (чем большее количество товаров в
потребительском наборе, тем выше его совокупная полезность для человека).Таким образом, если набор А содержит не меньше каждого товара, а одного из них больше, чем набор В, то А > В.
Слайд 37
5. Аксиома непрерывности
Любой товар может быть поделен
на сколь угодно мелкие единицы, так что размеры единиц,
в которых продается товар, не сдерживают потребителей;Если А > В, то наборы, близкие к А, также предпочтительнее набора В.
Слайд 38
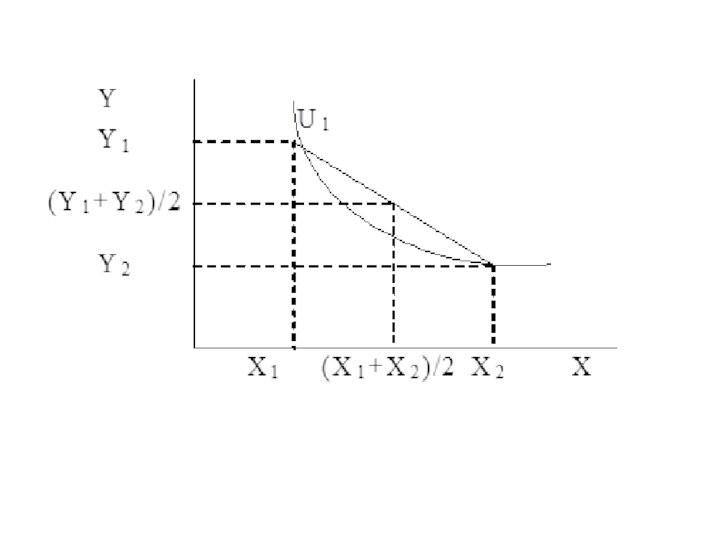
6. Аксиома строгой выпуклости к началу координат
Если
кривая безразличия строго выпукла к началу координат, то соединив
две любые точки, находящиеся внутри набора, отрезком прямой, получим, что комбинация (X1+X2)/ 2, (У1+У2)/2 предпочтительней любой из начальных комбинаций Х и Y, поскольку она будет находиться на более высокой кривой безразличия, чем исходные наборы.Слайд 40 Соблюдение вышеперечисленных предпосылок позволяет графически изобразить предпочтения с
помощью кривых безразличия свойства и виды которых весьма разнообразны.
Слайд 42 1. Кривая безразличия, лежащая выше и правее другой
кривой, представляет собой более предпочтительные для данного потребителя наборы
товаров.Рассмотрим на кривые безразличия I и II.
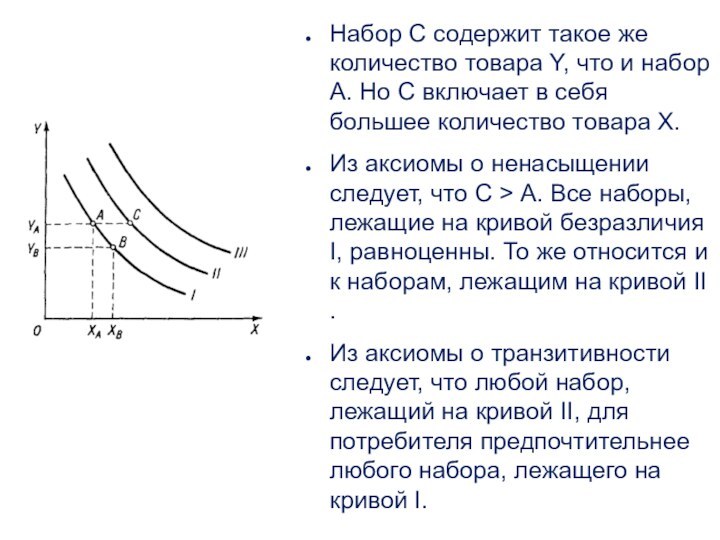
Слайд 43 Набор С содержит такое же количество товара Y,
что и набор А. Но С включает в себя
большее количество товара X.Из аксиомы о ненасыщении следует, что С > А. Все наборы, лежащие на кривой безразличия I, равноценны. То же относится и к наборам, лежащим на кривой II .
Из аксиомы о транзитивности следует, что любой набор, лежащий на кривой II, для потребителя предпочтительнее любого набора, лежащего на кривой I.
Слайд 44
2. Кривые безразличия имеют отрицательный наклон.
Пусть дана точка
А, характеризующая определенную комбинацию товаров. Проведем через нее две
взаимно перпендикулярные прямые.Слайд 45 Очевидно, что все точки, лежащие в III квадранте,
соответствуют большим, а все точки, лежащие в I квадранте,
– меньшим количествам товаров X и Y, чем точка А.В соответствии с аксиомой ненасыщения точки, лежащие в III квадранте, более предпочтительны, а лежащие в I квадранте – менее предпочтительны, чем А.
Следовательно, точки, безразличные А, например С, или В, или D, или G, должны находиться либо во II, либо в IV квадранте. И значит, кривая безразличия должна иметь отрицательный наклон.
Слайд 46
3. Кривые безразличия никогда не пересекаются.
Предположим противное.
Пусть кривые безразличия I и II пересеклись в точке
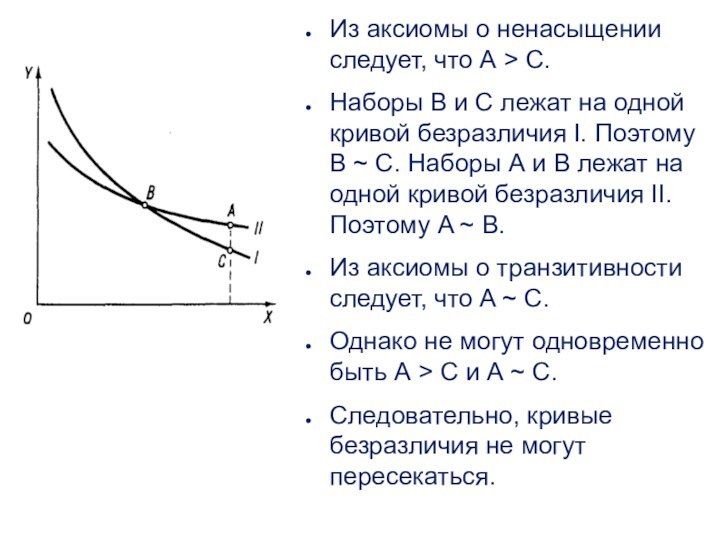
В.Слайд 47 Из аксиомы о ненасыщении следует, что А >
С.
Наборы В и С лежат на одной кривой
безразличия I. Поэтому В ~ С. Наборы А и В лежат на одной кривой безразличия II. Поэтому A ~ B. Из аксиомы о транзитивности следует, что A ~ С.
Однако не могут одновременно быть А > С и А ~ C.
Следовательно, кривые безразличия не могут пересекаться.
Слайд 48 4. Кривая безразличия может быть проведена через любую
точку пространства товаров.
Кривая безразличия не имеет «толщины». Это
свойство любых линий в Евклидовой геометрии, оно является, определенной абстракцией реального мира. Чтобы сделать его более реалистичным, необходимо при выборе единицы измерения товаров учитывать порог восприятия.
Слайд 49
5. Кривые безразличия выпуклы к началу координат.
Это
свойство, не может быть выведено непосредственно из аксиом рационального
поведения.Слайд 50 Основным рабочим понятием порядковой теории полезности является предельная
норма замещения благом X блага Y, которой называют количество
блага Y, которое должно быть сокращено «в обмен» на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным.Слайд 51 Норма, в которой человек готов заменить одно благо
на другое так, чтобы общий уровень его удовлетворенности остался
неизменным, называется предельной нормой замещения (marginal rate of substitution, MRS).Слайд 56 Предпочтения нормального вида являются гомотетичными (подобными), т.е. MRS
зависит только от соотношения благ в наборе (αY/βX), а
не от абсолютной величины объемов благ.Если потребитель предпочитает набор (X1,Y1) набору (X2,Y2), то для любого а>0 он предпочтет набор (аX1,аY1) набору (аХ2,аY2).
Слайд 57 2. Кривые безразличия для взаимозаменяемых товаров (совершенных
субститутов)
Функция полезности имеет вид:
U(X,Y)=aX+bY,
где а>0 и b>0,
параметры
MRSxy = k, где k – константа.
Если одна единица блага меняется на единицу другого блага, то MRSxy =1
Слайд 59 3. Кривые безразличия для взаимодополняемых благ (совершенных комплементов)
Функцию полезности для совершенных комплементов можно представить как
U(X,Y)=min{X,Y},
MRSxy=0, если товары дополняют друг друга в потреблении, то заменить один другим невозможно.
Слайд 61 4. Кривые безразличия для независимых (нейтральных, безразличных) благ,
или строгое предпочтение
Функцию полезности для набора (X,Y) c предпочитаемым
благом Х и с безразличным благом Y можно представить в виде U(X, Y)= U(Y), U(X)=0
Слайд 63 5. Благо и антиблаго или товары, нежелательные для
потребителя
К нежелательным (антиблагам) относятся товары, которые потребитель активно
не любит, но без которых в силу каких-либо причин не может обойтись.Степень удовлетворения потребителя и его оценка полезности будет тем выше, чем в меньших количествах нежелательный товар будет присутствовать в наборе.
Слайд 64 Функцию полезности для набора (X,Y) с благом Х
можно и антиблагом Y можно представить в виде
U(X,Y)=aX-bY,
где X – благо,
Y – антиблаго;
а>0 и b>0 – параметры.
Слайд 66 6. Несовместимые товары – эти товары лучше не
потреблять вместе.
Функцию полезности для набора (X.Y) можно представить в
виде U(X,Y)=X2+Y2
Слайд 68 7. Квазилинейные предпочтения – это такой случай,
когда все кривые безразличия являются "сдвигами" одной и той
же кривой безразличия.Квазилинейная, либо «частично линейная» функция полезности линейная по Y, но, может быть, нелинейная по X.
Линейная часть – продукт, потребляемый в относительно больших количествах в сопоставлении с нелинейным продуктом, потребление которого фактически не меняется.
Слайд 69 Функцию полезности для набора (X,Y) можно представить как
U(X,Y)= U(X)+ Y ,
где U(X) – нелинейная часть
функции полезности, Y – линейная часть функции полезности
Слайд 71
8. Лексикографические предпочтения
когда все потребительские наборы упорядочиваются
так же как слова в словаре: сначала по первой
координате, при совпадении первой координаты – по второй и т.д.Особенность лексикографических предпочтений – в невозможности быть представленными непрерывными кривыми безразличия.
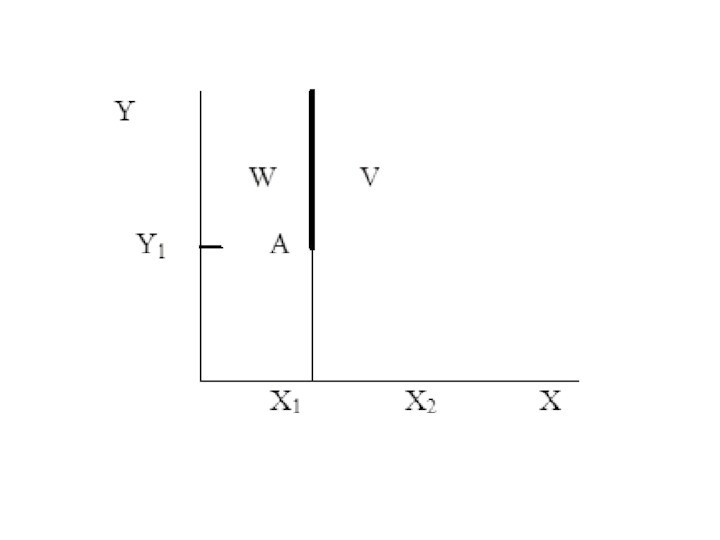
Слайд 73 Пусть потребительский набор состоит из двух товаров
– Х и Y. Тогда предпочтения потребителя таковы, что
если имеется два набора A=(Х1,Y1) и B=(X2,Y2) , то:а) Х1>Х2 ,подразумевает, что А > В,
б) X1 =Х2: и Y1 > Y2 подразумевают, что А > В.
Потребитель всегда предпочитает набор, в котором больше Х, независимо от количества Y; и только если оба набора содержат одинаковое количество Х, количество Y приобретает значение V.
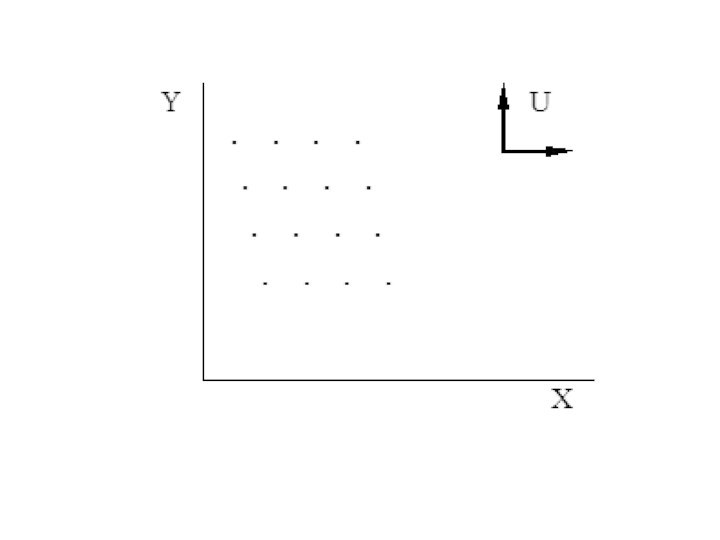
Слайд 74
9. Дискретные (неделимые) блага
Данный товар можно приобретать только
в неделимых количествах.
Функцию полезности для набора (X.Y) можно представить
в виде:U= f(X,Y),
где X – дискретный товар
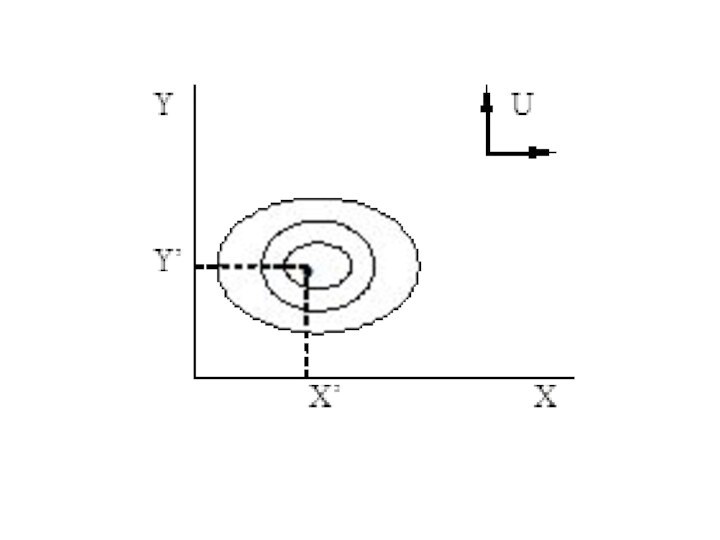
Слайд 76
10. Набор с точкой насыщения
Ситуация, при которой существует
идеальный потребительский набор, максимально удовлетворяющий потребности потребителя, то есть
находящийся в точке насыщенияГрафически кривые безразличия этого потребителя будут иметь вид эллипсов.
Слайд 78 Функцию полезности для набора (X.Y) можно представить в
виде
U=Z- (Х- Х`)2+(Y- Y`)2,
где Х и Y
– потребляемые товары, Х` и Y` – точки насыщения, т.е. объемы благ Х и Y, которые насыщают потребителя.
Z –максимальная полезность набора насыщения.





























