- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дедуктивные выводы из сложных суждений. Логика
Содержание
- 2. Тема: «Дедуктивные выводы из сложных суждений»Вопросы:Чисто условное и условно-категорическое умозаключенияРазделительно-категорическое умозаключениеУсловно-разделительное умозаключениеСокращенные, сложные и сложносокращенные силлогизмы
- 3. ЛитератураКириллов В.И., Старченко А.А. Логика: Учебник. М.:
- 4. Электронно-библиотечная система IPRbooksОсновнаяДемидов И.В. Логика: Учебник. −
- 5. Литература ЭБС «Лань» http://e.lanbook.comДмитревская, И.В. Логика
- 6. ЧИСТО УСЛОВНОЕ УМОЗАКЛЮЧЕНИЕЧисто условное умозаключение - это умозаключение, посылки и заключение которого являются условными суждениями.
- 7. Схема чисто условного умозаключения(p→q) ∧ (q→r)p→rВывод основывается на правиле: следствие следствия (r) есть следствие основания (p).
- 8. Пример чисто условного умозаключенияЕсли будет финансовый кризис,
- 9. Условно-категорическое умозаключениеУсловно-категорическое умозаключение – это умозаключение, в
- 10. Утверждающий модус
- 11. Отрицающий модус
- 12. Неправильные модусы p→q,
- 13. Примеры неправильных модусовЕсли будет засуха, то посевы
- 14. Правильные модусы условно-категорического умозаключенияподчиняются правилу: утверждение основания
- 15. Однако, если большая посылка является эквивалентным суждением:
- 16. Разделительно-категорическое умозаключениеРазделительно-категорическое умозаключение – это умозаключение, в
- 17. Утверждающе-отрицающий модус (modus ponendo tollens)
- 18. Отрицающе-утверждающий модус (modus tollendo ponens) ,
- 19. Пример разделительно-категорического умозаключенияДоговор может быть двусторонним или многосторонним.Заключенный договор не является многосторонним.Заключенный договор является двусторонним.
- 20. Условно-разделительное умозаключениеУмозаключение, в котором одна посылка условное,
- 21. Виды дилеммРазличают следующие виды дилемм: конструктивная (созидательная)простаясложнаядеструктивная (разрушительная)простаясложная
- 22. Простая конструктивная дилеммаВ простой конструктивной дилемме условная
- 23. Пример простой конструктивной дилеммы:Если будет туман, то
- 24. Сложная конструктивная дилеммаВ сложной конструктивной дилемме условная
- 25. Пример сложной конструктивной дилеммы:Если осуществляется передача недвижимости
- 26. Простая деструктивная дилеммаВ простой деструктивной дилемме условная
- 27. Пример простой деструктивной дилеммы:Если будет наводнение, то
- 28. Сложная деструктивная дилеммаВ сложной деструктивной дилемме условная
- 29. Пример сложной деструктивной дилеммы:Если организация является коммерческой,
- 30. Сокращенный силлогизм (энтимема)Силлогизм, в котором выражены
- 31. Например:«Экономика является наукой, следовательно она имеет предмет
- 32. Форму энтимемы принимают также умозаключения, посылками которых
- 33. Сложный силлогизмСоединение простых силлогизмов,
- 34. Прогрессивный и регрессивный полисиллогизмыВ прогрессивном полисиллогизме заключение
- 35. Пример прогрессивного полисиллогизмаВсе китообразные животные – млекопитающиеДельфины
- 36. Пример регрессивного полисиллогизмаВсе китообразные животные – млекопитающиеДельфины
- 37. Сложными могут быть чисто условные силлогизмы, которые
- 38. Не было гвоздя - Подкова пропала, Не
- 39. СОРИТСорит (греч. куча) – полисиллогизм, в котором
- 40. Пример соритаКража есть хищение чужого имуществаХищение чужого
- 41. ЭпихейремаК сложносокращенным силлогизмам относится также эпихейрема. Эпихейремой
- 42. Скачать презентацию
- 43. Похожие презентации




![Дедуктивные выводы из сложных суждений. Логика Литература ЭБС «Лань» http://e.lanbook.comДмитревская, И.В. Логика [Электронный ресурс]: учебное пособие. −](/img/tmb/15/1449753/90274b65f9ae1c5032e832f153821c1b-720x.jpg)































Слайд 2
Тема: «Дедуктивные выводы из сложных суждений»
Вопросы:
Чисто условное и
условно-категорическое умозаключения
Слайд 3
Литература
Кириллов В.И., Старченко А.А. Логика: Учебник. М.: Проспект,
2014.
Кириллов В.И., Орлов Г.А., Фокина Н.И. Упражнения по логике.
М.: Проспект,2014. URL: http://e.lanbook.com/books/ element.php?pl1_id=54814. − ЭБС «Лань».Мирошниченко Л.Н. Логика: Учебно-методическое пособие. Красногорск, 2013.
Слайд 4
Электронно-библиотечная система IPRbooks
Основная
Демидов И.В. Логика: Учебник. − М.:
Дашков и Ко,2012. − 348 с. − URL: http://www.iprbookshop.ru/10936.html.
Дополнительная
Светлов
В.А. Логика: Учебное пособие. − М.: Логос,2012. − 432 с. − URL: http://www.iprbookshop.ru/9134.html.Дегтярев М.Г., Хмелевская С.А. Логика: Учебник для студентов юридических вузов. − М.: Пер Сэ, 2012. − 288 с. − URL: http://www.iprbookshop.ru/7412.html.
Гриценко В.П. Логика: Учебное пособие. − Краснодар: Южный институт менеджмента,2012. − 265 с. − URL: http://www.iprbookshop.ru/10288.html.
Слайд 5
Литература
ЭБС «Лань»
http://e.lanbook.com
Дмитревская, И.В. Логика [Электронный ресурс]: учебное
пособие. − Электрон. дан. − М.: ФЛИНТА, 2013. −
384 с. − Режим доступа: http://e.lanbook.com/ books/element.php?pl1_id=71956 − ЭБС «Лань».Ивлев, Ю.В. Логика [Электронный ресурс]: учебник. − Электрон. дан. − М.: Проспект, 2015. − 297 с. − URL: http://e.lanbook.com/books/element.php?pl1_id=54781. − ЭБС «Лань».
Слайд 6
ЧИСТО УСЛОВНОЕ УМОЗАКЛЮЧЕНИЕ
Чисто условное умозаключение - это умозаключение,
посылки и заключение которого являются условными суждениями.
Слайд 7
Схема чисто условного умозаключения
(p→q) ∧ (q→r)
p→r
Вывод основывается на
правиле: следствие следствия (r) есть следствие основания (p).
Слайд 8
Пример чисто условного умозаключения
Если будет финансовый кризис, то
наступит инфляция
В случае возникновения инфляции произойдет обесценивание денег
_______________________________________________________
Если будет
финансовый кризис, то произойдет обесценивание денег
Слайд 9
Условно-категорическое умозаключение
Условно-категорическое умозаключение – это умозаключение, в котором
одна из посылок – условное, а другая посылка и
заключение – категорические суждения.Это умозаключение имеет два правильных модуса: утверждающий и отрицающий. Они дают достоверные выводы.
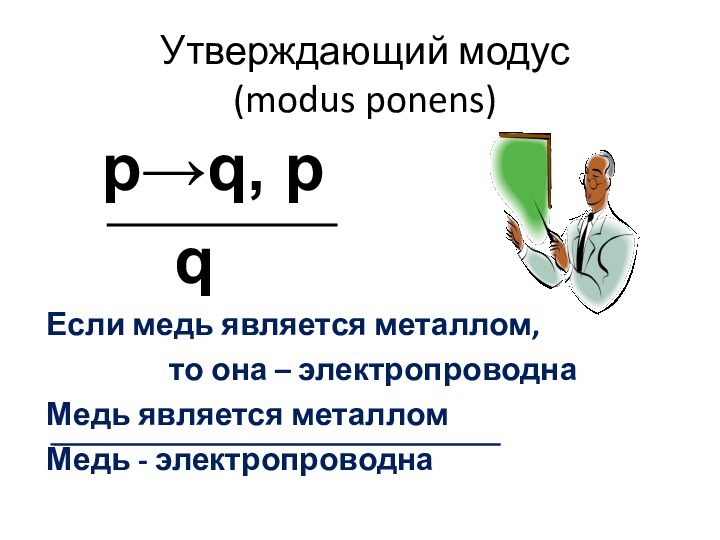
Слайд 10 Утверждающий модус
(modus ponens)
p→q, p
qЕсли медь является металлом,
то она – электропроводна
Медь является металлом
Медь - электропроводна
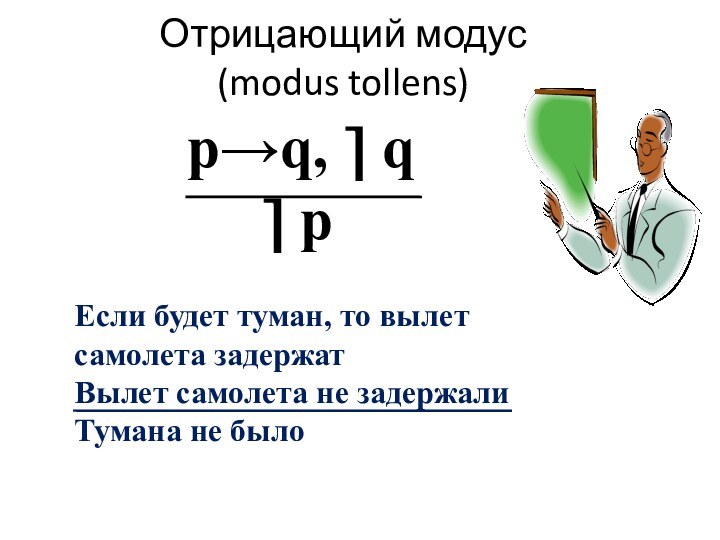
Слайд 11 Отрицающий модус
(modus tollens)
p→q, ⎤ q
⎤ p Если будет туман, то вылет самолета задержат
Вылет самолета не задержали
Тумана не было
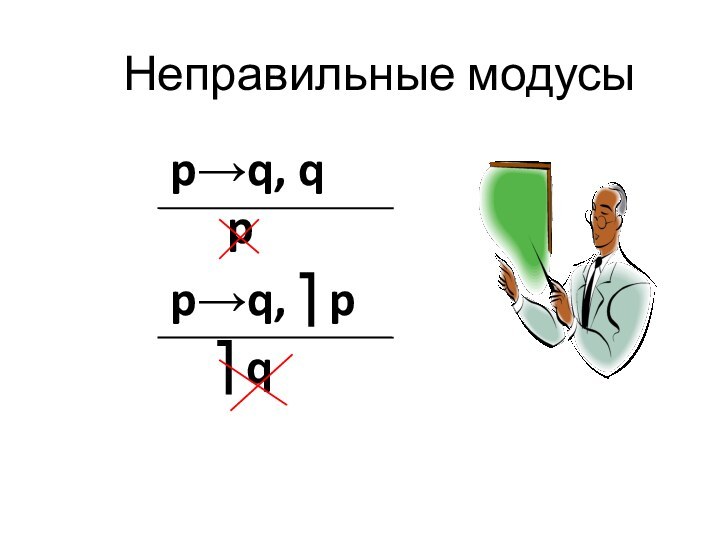
Слайд 13
Примеры неправильных модусов
Если будет засуха, то посевы погибнут
Посевы
погибли
Была засуха
Если будет засуха, то посевы погибнут
Засухи не было
Посевы
не погибли
Слайд 14
Правильные модусы условно-категорического умозаключения
подчиняются правилу: утверждение основания ведет
к утверждению следствия и отрицание следствия – к отрицанию
основания.Неправильные модусы подчиняются правилу: отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.
Слайд 15 Однако, если большая посылка является эквивалентным суждением: р
≡ q (если и только если р, то q),
то достоверные заключения получаются по всем четырем модусам:р ≡ q, p р ≡ q, ⎤ q р ≡ q, q р ≡ q, ⎤ p
q ⎤ р р ⎤ q
Если сегодня вторник, то завтра – среда
Завтра будет среда
Следовательно, сегодня - вторник
Слайд 16
Разделительно-категорическое умозаключение
Разделительно-категорическое умозаключение – это умозаключение, в котором
одна из посылок – разделительное, а другая посылка и
заключение – категорические суждения.Это умозаключение имеет два модуса:
утверждающе-отрицающий и отрицающе-утверждающий.
Слайд 17
Утверждающе-отрицающий модус (modus ponendo tollens)
p ∨ q,
p⎤ q
Заключение по этому модусу достоверно, если соблюдается правило: разделительная посылка должна быть исключающе-разделителъным суждением, или суждением строгой дизъюнкции
Слайд 18
Отрицающе-утверждающий модус (modus tollendo ponens)
, ⎤
p
q
Заключение по этому модусу достоверно, если соблюдается правило: в
разделительной посылке должны быть перечислены все возможные суждения – дизъюнкты, иначе говоря, эта посылка должна быть полным (закрытым) дизъюнктивным высказыванием.
Слайд 19
Пример разделительно-категорического умозаключения
Договор может быть двусторонним или многосторонним.
Заключенный
договор не является многосторонним.
Заключенный договор является двусторонним.
Слайд 20
Условно-разделительное умозаключение
Умозаключение, в котором одна посылка условное, а
другая – разделительное суждение, называется условно-разделительным, или лемматическим (лемма
– предположение).Разделительное суждение может содержать две, три и большее число альтернатив, поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтернативы) и т. д.
Слайд 21
Виды дилемм
Различают следующие виды дилемм:
конструктивная (созидательная)
простая
сложная
деструктивная (разрушительная)
простая
сложная
Слайд 22
Простая конструктивная дилемма
В простой конструктивной дилемме условная посылка
содержит два основания, из которых вытекает одно следствие. Разделительная
посылка утверждает оба возможных основания, заключение утверждает следствие.(p→ r) ∧ (q→r), p ∨ q
r
Слайд 23
Пример простой конструктивной дилеммы:
Если будет туман, то вылет
самолета задержат
Если будет сильный снегопад, то вылет самолета тоже
задержатБыл туман или сильный снегопад
Вылет самолета задержали
Слайд 24
Сложная конструктивная дилемма
В сложной конструктивной дилемме условная посылка
содержит два основания и два следствия. Разделительная посылка утверждает
оба возможных основания.Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствий.
(p→ r) ∧ (q→s), p ∨ q
r ∨ s
Слайд 25
Пример сложной конструктивной дилеммы:
Если осуществляется передача недвижимости в
собственность, то заключается договор в письменной форме
Если оказывается услуга
по ремонту недвижимости, то договор может быть заключен в устной формеНедвижимость либо передана в собственность, либо осуществляется ремонт
Заключен договор либо в письменной, либо в устной форме
Слайд 26
Простая деструктивная дилемма
В простой деструктивной дилемме условная посылка
содержит одно основание, из которого вытекает два возможных следствия.
Разделительная посылка отрицает оба следствия, заключение отрицает основание. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности основания.(p→ q) ∧ (p→r), ⎤ q ∨ ⎤ r
⎤ p
Слайд 27
Пример простой деструктивной дилеммы:
Если будет наводнение, то объявляется
режим ЧП
Если будет наводнение, то производится эвакуация населения
Режим ЧП
не объявлен или эвакуация населения не производиласьНаводнения не было
Слайд 28
Сложная деструктивная дилемма
В сложной деструктивной дилемме условная посылка
содержит два основания и два следствия. Разделительная посылка отрицает
оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.(p→ q) ∧ (r → s), ⎤ q ∨ ⎤ s
⎤ p ∨ ⎤ r
Слайд 29
Пример сложной деструктивной дилеммы:
Если организация является коммерческой, то
основная цель ее деятельности – извлечение прибыли
Если организация является
кооперативом, то она осуществляет деятельность на основе добровольного объединения гражданДанная организация не ставит основной целью извлечение прибыли или не осуществляет деятельность на основе добровольного объединения граждан
Данная организация не является коммерческой или кооперативом
Слайд 30
Сокращенный силлогизм (энтимема)
Силлогизм, в котором выражены
все его части – обе посылки и заключение, называется полным.
Силлогизм с пропущенной посылкой или заключением называется сокращенным силлогизмом, или энтимемой (греч. «в уме»).
Широко используются энтимемы простого категорического силлогизма, особенно выводы по первой фигуре.
Слайд 31
Например:
«Экономика является наукой, следовательно она имеет предмет изучения».
Полный
силлогизм строится по
1-й фигуре:Все науки (М) имеют предмет изучения (Р)
Экономика (S) является наукой (М)
_______________________________________________________________________________________________________________________________
Экономика (S) имеет предмет изучения (Р)
Слайд 32 Форму энтимемы принимают также умозаключения, посылками которых являются
условные и разделительные суждения. Например, «Вылет самолета был задержан,
так как был туман».Использование сокращенных силлогизмов обусловлено тем, что пропущенная посылка или заключение либо содержит известное положение, которое не нуждается в устном или письменном выражении, либо в контексте выраженных частей умозаключения она легко подразумевается.
Слайд 33
Сложный силлогизм
Соединение простых силлогизмов,
в котором заключение
предшествующего силлогизма становится посылкой последующего силлогизма, называется сложным силлогизмом, или полисиллогизмом.
Слайд 34
Прогрессивный и регрессивный полисиллогизмы
В прогрессивном полисиллогизме заключение предшествующего
силлогизма становится большей посылкой последующего.
В регрессивном полисиллогизме заключение предшествующего
силлогизма становится меньшей посылкой последующего.
Слайд 35
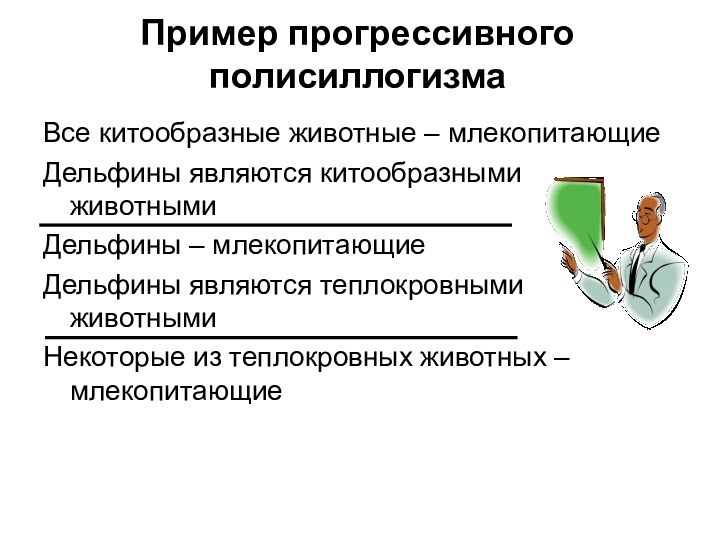
Пример прогрессивного полисиллогизма
Все китообразные животные – млекопитающие
Дельфины являются
китообразными животными
Дельфины – млекопитающие
Дельфины являются теплокровными животными
Некоторые из теплокровных
животных – млекопитающие
Слайд 36
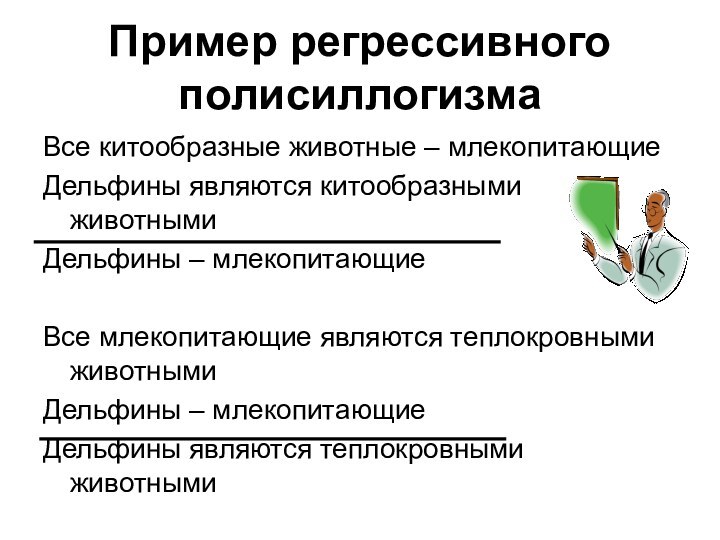
Пример регрессивного полисиллогизма
Все китообразные животные – млекопитающие
Дельфины являются
китообразными животными
Дельфины – млекопитающие
Все млекопитающие являются теплокровными животными
Дельфины –
млекопитающиеДельфины являются теплокровными животными
Слайд 37 Сложными могут быть чисто условные силлогизмы, которые имеют
схему:
(p→q) ∧ (q→r) ∧ … ∧ (r →s)
p→s
Из схемы
видно, что, как и в простом чисто условном умозаключении, заключение представляет собой импликативную связь основания первой посылки со следствием последней.Слайд 38 Не было гвоздя - Подкова пропала, Не было подковы - Лошадь
захромала, Лошадь захромала - Командир убит, Конница разбита, Армия бежит! Враг вступает в город, Пленных
не щадя, Оттого, что в кузнице Не было гвоздя!
Слайд 39
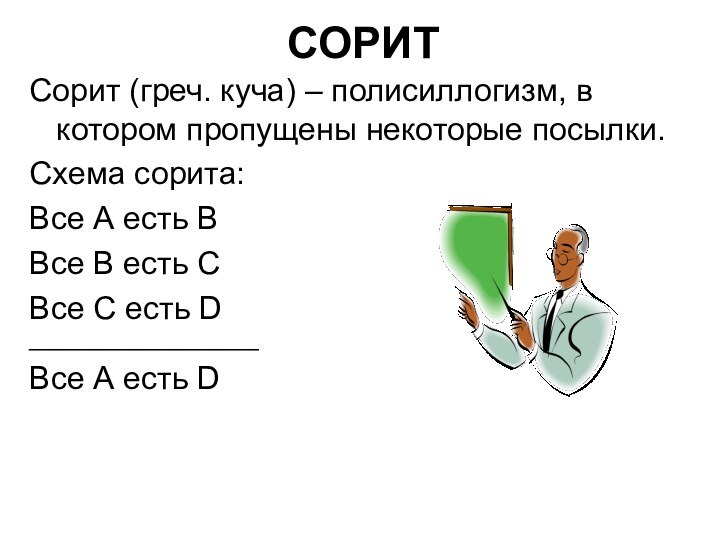
СОРИТ
Сорит (греч. куча) – полисиллогизм, в котором пропущены
некоторые посылки.
Схема сорита:
Все А есть В
Все В есть С
Все
С есть D_______________________
Все А есть D
Слайд 40
Пример сорита
Кража есть хищение чужого имущества
Хищение чужого имущества
есть преступление
Преступление есть общественно опасное деяние
_________________________________
Кража есть общественно опасное
деяние
Слайд 41
Эпихейрема
К сложносокращенным силлогизмам относится также эпихейрема. Эпихейремой называется
сложносокращенный
силлогизм, обе посылки которого являются энтимемами.Все А суть С, так как А суть В.
Все D суть А, так как D суть Е.
______________________
Все D суть С.