Презентация на тему Электронное пособие по теме Плоская система сходящихся сил

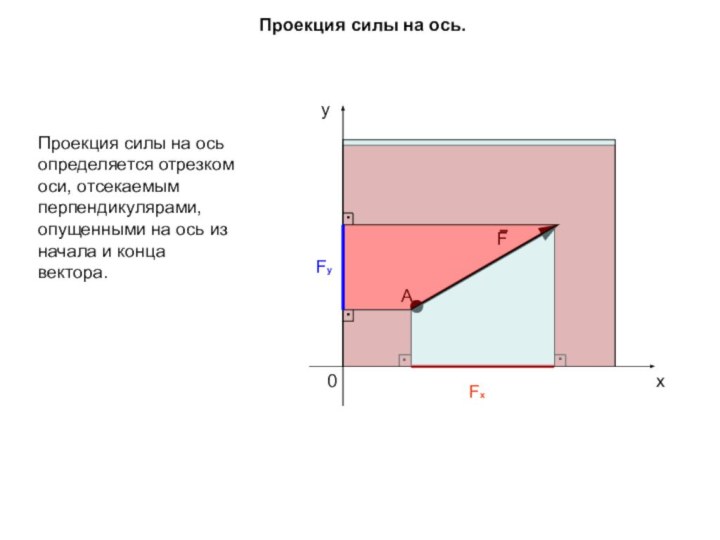
отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала

0

силы на косинус угла между вектором силы и положительным

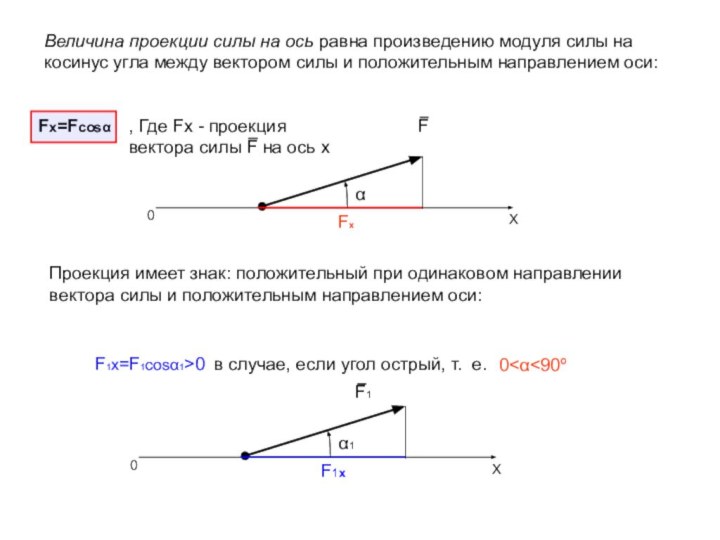
Проекция имеет знак: положительный при одинаковом направлении вектора силы и положительным направлением оси:

X

F1

α1

0

F1x=F1cosα1>0

F1x

0<α<90º

, Где Fx - проекция вектора силы F на ось x

в случае, если угол острый, т. е.

отрицательной полуоси:
F2
α2
0
β2
F2x

F2x= F2cosα2 = -F2cosβ
cosα2= cos(180º-β2) = -cosβ2
90º

x

0

.

F3

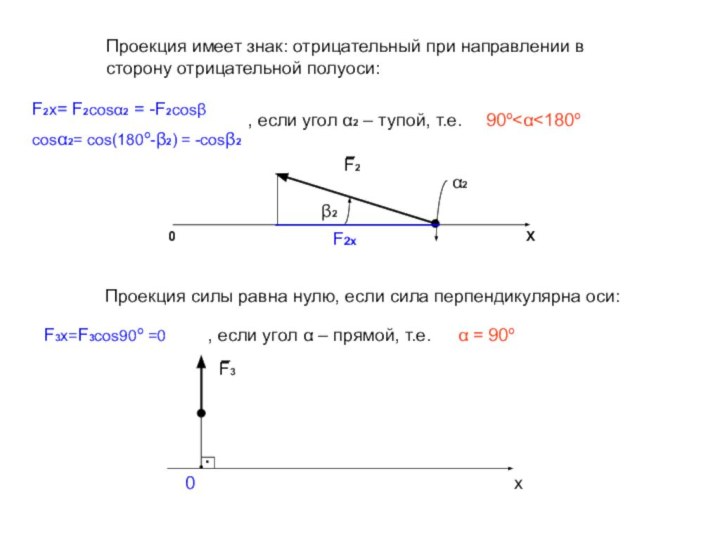
α = 90º

F3x=F3cos90º =0

, если угол α2 – тупой, т.е.

, если угол α – прямой, т.е.

многоугольника.
F1
F2
F3
F4
А

Спроектируем векторное равенство на ось x :
Спроектируем векторное

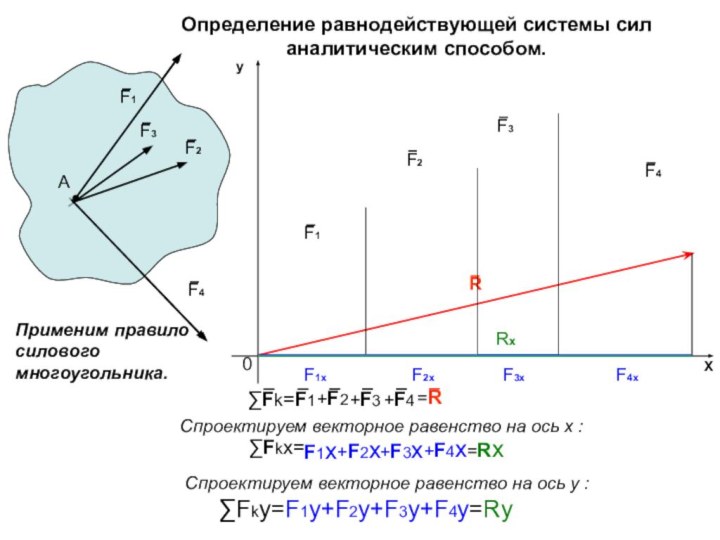
∑Fky=F1y+F2y+F3y+F4y=Ry

∑Fk=F1

+F2

+F3

+F4

=R

∑Fkx=

+F2x

+F3x

+F4x

=Rx

F1x

алгебраической сумме проекций всех сил системы на эти оси:


Модуль

R=√ R x+R y

2

2

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат:

cosαx=

Rx

R

cosαy=

Ry

R

R

αx

αy

Rx

X

y

0

Ry

форме.
Исходя из того, что равнодействующая равна нулю, получим
R=√

2

2

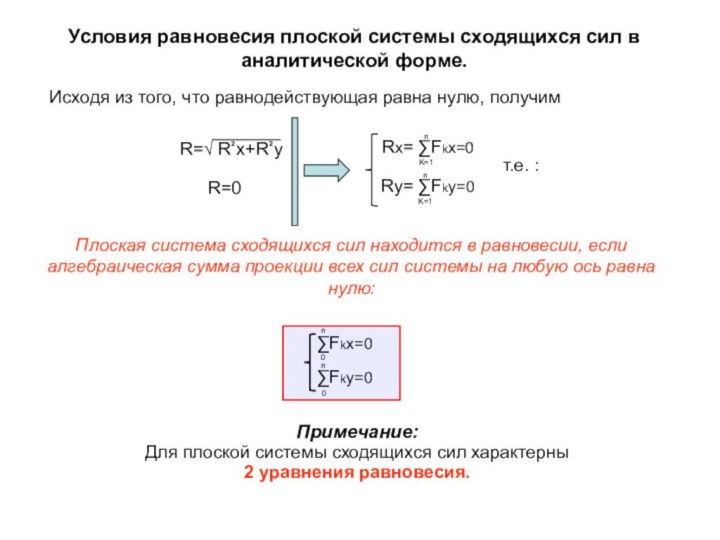
Rx= ∑Fkx=0

n

K=1

Ry= ∑Fky=0

n

K=1

R=0

т.е. :

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекции всех сил системы на любую ось равна нулю:

∑Fkx=0

n

0

∑Fky=0

n

0

Примечание:
Для плоской системы сходящихся сил характерны
2 уравнения равновесия.

статики на равновесие решаются в строгом порядке:
1. Выбирается объект

2. На основании аксиомы связей мысленно освободить несвободное тело от связей, заменив их действием реакциями.

3. К выбранному объекту приложить все действующие активные силы, в том числе и силы тяжести.

4. К полученной системе сил применить условия равновесия в геометрической или аналитической форме. При этом, геометрический метод решения применяется в случае, если на объект действует система 3х сходящихся сил; тогда строится и затем решается (графически или геометрически) замкнутый силовой треугольник.

Аналитический метод применяется в случае, если число действующих на объект сил от 3х и больше, или силы не лежат в одной плоскости

5. Определяются искомые величины, и полученные результаты исследуются.

Примечание:

В случае применения аналитического метода решения необходимо: а) выбрать оси координат так, чтобы одна из неизвестных реакций была направлена вдоль оси; б) произвести проверку правильности решения, для чего, выбрав новую систему координат, составить аналитические уравнения равновесия

подвешен на нити м опирается о гладкую стену.
Решение:
1.

2. Мысленно отбрасываем связи (связями являются тела, устранив которые, несвободное тело превратится в свободное) – нить и стена.

Реакция нити направлена вдоль нити – Т,

N

T

3. Прикладываем активную силу – силу тяжести mg

mg

4. Задачу решаем аналитически. Для этого прикладываем систему координат xOy в центре шара так, чтобы одна из неизвестных, например N,была направлена вдоль оси x.

x

y

Перенесем реакции Т и N в точку О (согласно следствию аксиомы присоединения или отбрасывания).

О

300

Определить силу натяжения нити и
реакцию опорной поверхности.

реакция стены направлена перпендикулярно опорной поверхности – N (в сторону, противоположную возможному перемещению).

и осью y согласно условию задачи равен 300
Для

∑Fkx=0

n

0

∑Fky=0

n

0

(1)

(2)

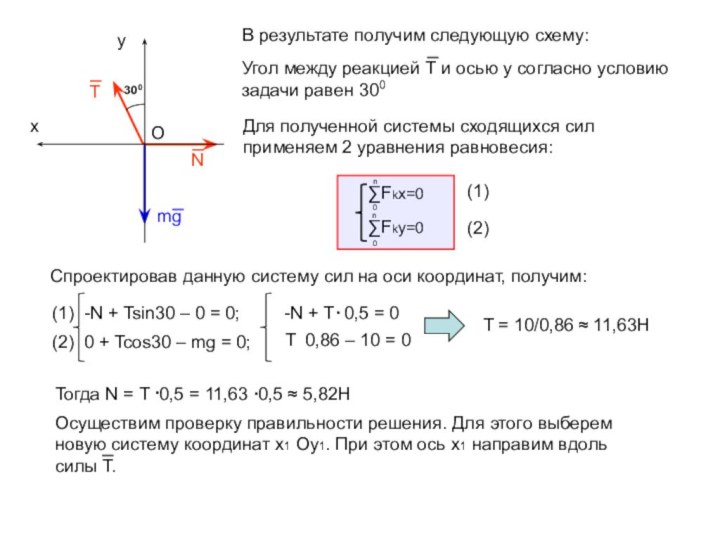
Спроектировав данную систему сил на оси координат, получим:

(1) -N + Tsin30 – 0 = 0;

(2) 0 + Tcos30 – mg = 0;

-N + T 0,5 = 0

T 0,86 – 10 = 0

T = 10/0,86 ≈ 11,63H

Тогда N = T 0,5 = 11,63 0,5 ≈ 5,82H

Осуществим проверку правильности решения. Для этого выберем новую систему координат x1 Oy1. При этом ось x1 направим вдоль силы Т.

300

.

.

.