- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Закон всемирного тяготения
Содержание
- 2. НЬЮТОН (Newton) Исаак (1643–1727), английский математик, механик,
- 3. Исаак Ньютон похоронен в Вестминстерском аббатстве. Над
- 4. Ньютон смог объяснить движение тел в космическом
- 5. Если m1 и m2 – массы двух
- 6. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ Два любых тела притягиваются
- 7. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ Открыт Ньютоном в 1667
- 8. Закон справедлив для:Однородных шаров. Для материальных точек.
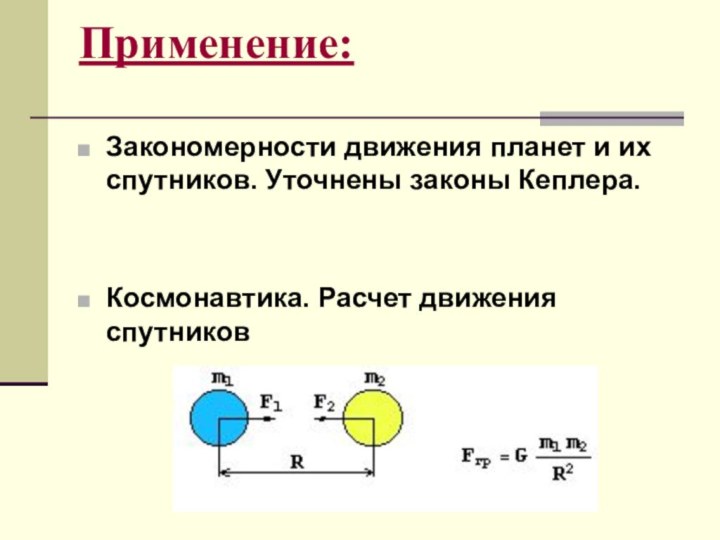
- 9. Применение: Закономерности движения планет и их спутников. Уточнены законы Кеплера. Космонавтика. Расчет движения спутников
- 10. Силы тяготения или иначе гравитационные силы, действующие
- 11. Внимание!:Закон не объясняет причин тяготения, а только
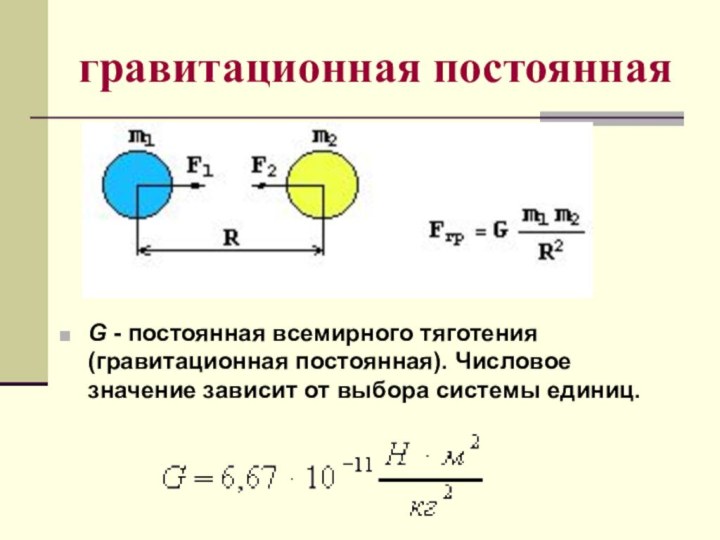
- 12. гравитационная постояннаяG - постоянная всемирного тяготения (гравитационная постоянная). Числовое значение зависит от выбора системы единиц.
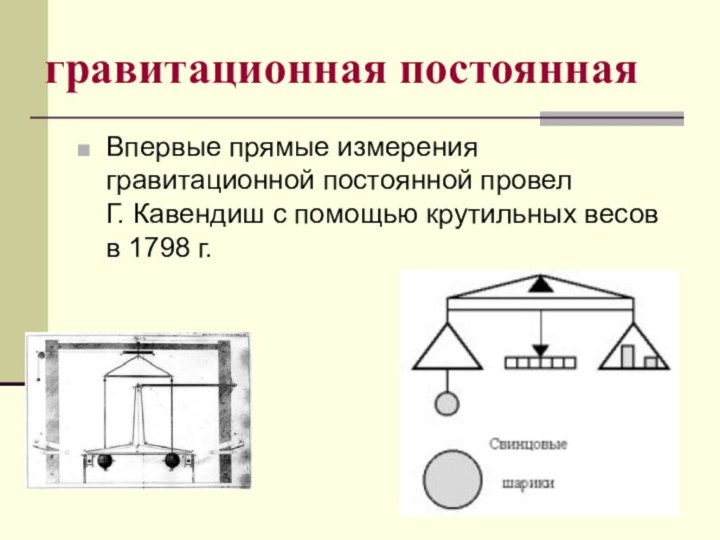
- 13. гравитационная постояннаяВпервые прямые измерения гравитационной постоянной провел
- 14. Физический смысл гравитационной постоянной: гравитационная постоянная численно
- 15. ЭТО ИНТЕРЕСНОЕсли изменить постоянную тяготения, скажем увеличить
- 16. ЭТО ИНТЕРЕСНОЗемля отстоит от Солнца на 150
- 18. Пусть m1=m2=1 кг, R=1 м, тогда: G=F
- 19. Ускорение, которое испытывает тело m, находящееся на
- 20. Скачать презентацию
- 21. Похожие презентации
НЬЮТОН (Newton) Исаак (1643–1727), английский математик, механик, астроном и физик, создатель классической механики, член (1672) и президент (с 1703) Лондонского королевского общества.
















Слайд 3
Исаак Ньютон похоронен в Вестминстерском аббатстве. Над его
могилой высится памятник с бюстом и эпитафией «Здесь покоится
сэр Исаак Ньютон, дворянин, который почти божественным разумом первый доказал с факелом математики движение планет, пути комет и приливы океанов. Он исследовал различие световых лучей и проявляющиеся при этом различные свойства цветов... Пусть смертные радуются, что существует такое украшение рода человеческого».Слайд 4 Ньютон смог объяснить движение тел в космическом пространстве
с помощью закона всемирного тяготения.
Ньютон пришел к своей
теории в результате многолетних исследований движения Луны и планет. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Слайд 5 Если m1 и m2 – массы двух точечных
тел, а r – расстояние между ними, то закон
всемирного тяготения записывается в видегде G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная.
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Слайд 6
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Два любых тела притягиваются друг
к другу с силой, прямо пропорциональной произведению масс этих
тел и обратно пропорционально квадрату расстояния между ними.
Слайд 7
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Открыт Ньютоном в 1667 году
на основе анализа движения планет (з-ны Кеплера) и, в
частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович.
Слайд 8
Закон справедлив для:
Однородных шаров.
Для материальных точек.
Для
концентрических тел.
если одно тело большой шар , а другое
находится вблизи негоГравитационное взаимодействие существенно при взаимодействии тел большой массы.
Слайд 9
Применение:
Закономерности движения планет и их спутников. Уточнены
законы Кеплера.
Космонавтика. Расчет движения спутников
Слайд 10 Силы тяготения или иначе гравитационные силы, действующие между
двумя телами: - дальнодействующие; - для них не существует преград; -
направлены вдоль прямой, соединяющей тела; - равны по величине; - противоположны по направлению.Анализ закона:
Слайд 11
Внимание!:
Закон не объясняет причин тяготения, а только устанавливает
количественные закономерности.
В случае взаимодействия трех и более тел
задачу о движении тел нельзя решить в общем виде. Требуется учитывать "возмущения", вызванные другими телами (открытие Нептуна Адамсом и Леверье в 1846 г. и Плутона в 1930). В случае тел произвольной формы требуется суммировать взаимодействия между малыми частями каждого тела.
Слайд 12
гравитационная постоянная
G - постоянная всемирного тяготения (гравитационная постоянная).
Числовое значение зависит от выбора системы единиц.
Слайд 13
гравитационная постоянная
Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш
с помощью крутильных весов в 1798 г.
Слайд 14 Физический смысл гравитационной постоянной: гравитационная постоянная численно равна модулю
силы тяготения, действующей между двумя точечными телами массой по
1 кг каждое, находящимися на расстоянии 1 м друг от друга.гравитационная постоянная
Слайд 15
ЭТО ИНТЕРЕСНО
Если изменить постоянную тяготения, скажем увеличить ее
на 10 процентов, что произойдет?
Сократится радиус земной орбиты,
увеличится количество тепла, поступающего на Землю от Солнца. Температура Земли, как показывают расчеты физиков, подскочит на 100 градусов. Резко изменится и угрожающе изменится климат/ В подобных условиях существование на Земле высокоорганизованной органической материи стало бы по-видимому, невозможным.___
Слайд 16
ЭТО ИНТЕРЕСНО
Земля отстоит от Солнца на 150 миллионов
километров. Случайность?
Вовсе нет. Именно здесь центробежная сила (вращение
Земли вокруг Солнца) уравновешивается силой притяжения. Вот так ход планетам диктует постоянная тяготения, входящая в данный нам Ньютоном закон.





























