Презентация на тему Атомная физика

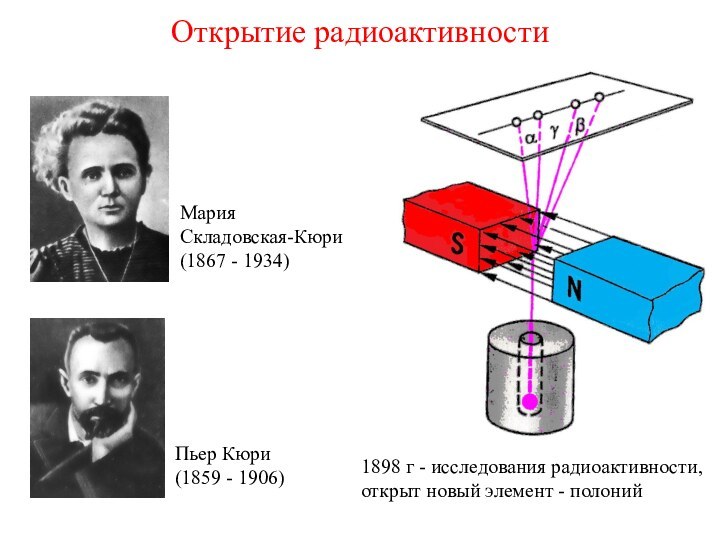
Беккерель изучал термоэлектричество и флуоресценцию. Его отец, Александр Эдмон

1 марта 1896 г.

- полоний

частицы, чтобы сохранять устойчивую конфигурацию, должны двигаться.
В этом и

Здесь электроны - кольца вокруг положительно заряженного тела. Но

- планетарная. Но никаких физческих обоснований она не имела.

фермера-скотовода. С 1895 г. работал в Кавендишской лаборатории. Был

α-частицы со скоростью 10 - 20 тысяч километров в

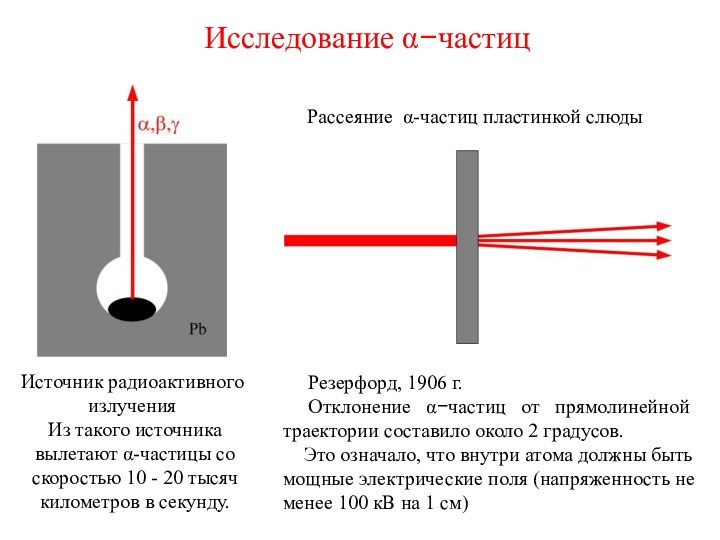
Рассеяние α-частиц пластинкой слюды

Резерфорд, 1906 г.
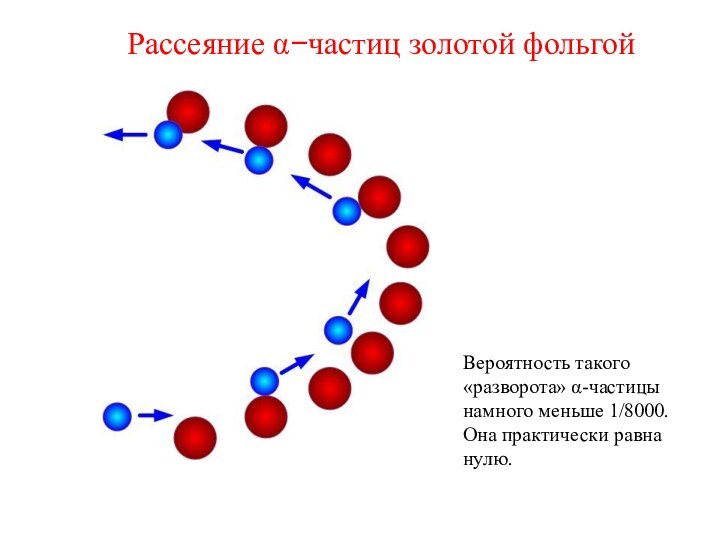
Отклонение α−частиц от прямолинейной траектории составило около 2 градусов.
Это означало, что внутри атома должны быть мощные электрические поля (напряженность не менее 100 кВ на 1 см)

Установлено, что одна из примерно 8000 α−частиц рассеивается на

невероятно, как если бы вы выстрелили 15-дюймовым снарядом в

1/8000.
Она практически равна нулю.

на большие углы было наличие массивного, хотя и очень

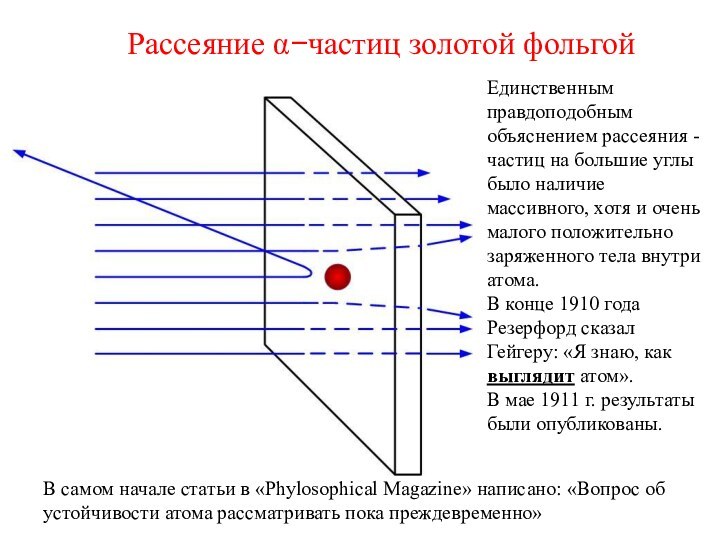
В самом начале статьи в «Phylosophical Magazine» написано: «Вопрос об устойчивости атома рассматривать пока преждевременно»

существовать не может:
- электроны движутся по замкнутым траекториям, следовательно,

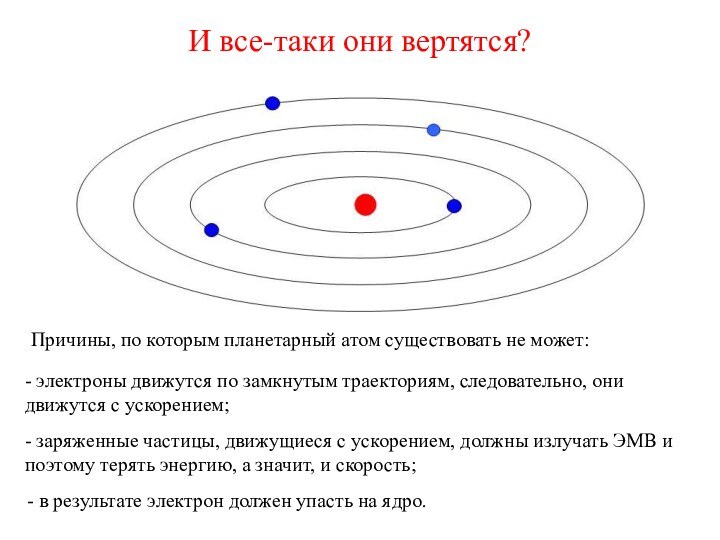
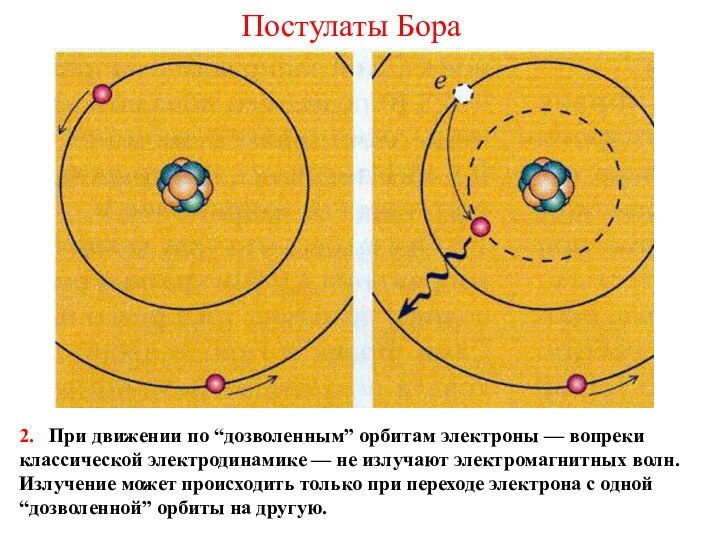
- заряженные частицы, движущиеся с ускорением, должны излучать ЭМВ и поэтому терять энергию, а значит, и скорость;

- в результате электрон должен упасть на ядро.

чтобы объяснить, как может существовать планетарный атом Резерфорда, Бор

2. Он обратил внимание на то, что постоянная Планка h имеет размерность (в системе СИ, которой тогда не было, Дж·с), совпадающую с размерностью физической величины, называемой действием.

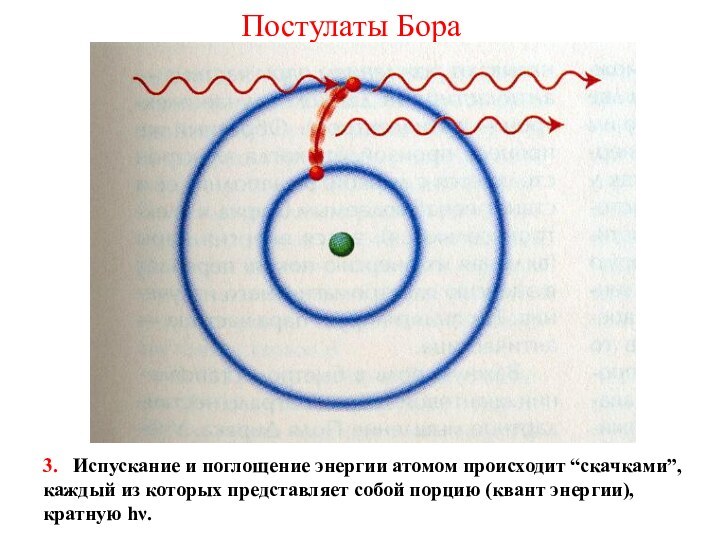
3. Бор предположил, что все физические величины должны изменяться так, что в ходе любых процессов действие должно быть равно целому числу постоянных Планка h.

4. Основываясь на предположении о квантовании (скачкообразном изменении) действия, Бор предположил, что при движении электрона по орбите вокруг положительного заряженного ядра выполняется условие
2π RmV=nh,
то есть квантуется действие электрона.

происходит порциями – квантами, энергия которых равна
Изменение энергии стоячей

Стоячие волны можно рассматривать, как линейные гармонические осцилляторы. Согласно Планку, из всех возможных состояний линейного гармонического осциллятора осуществляются только такие, энергия которых

где n – целое число.

Перепишем последнее условие в виде

Это означает, что некоторая величина, имеющая размерность [энергия/частота] или [энергия∙время] должна быть кратной постоянной Планка. Эта величина называется действием.

приводящее к правильному выбору состояний, рассмотрим линейный гармонический осциллятор.

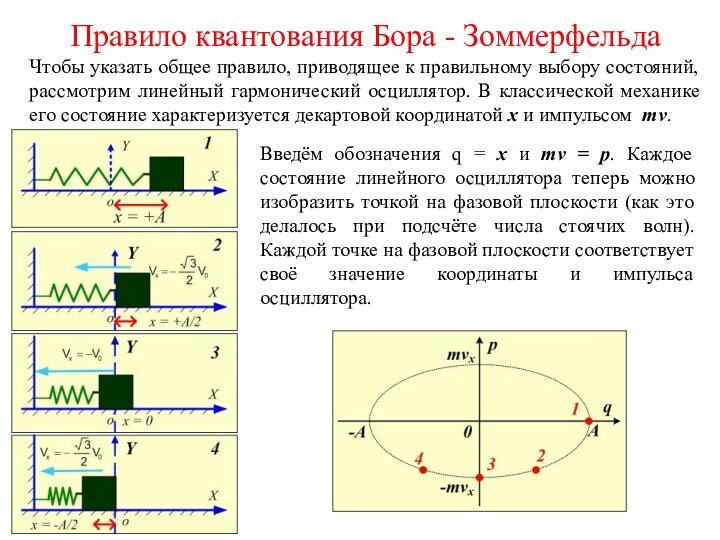
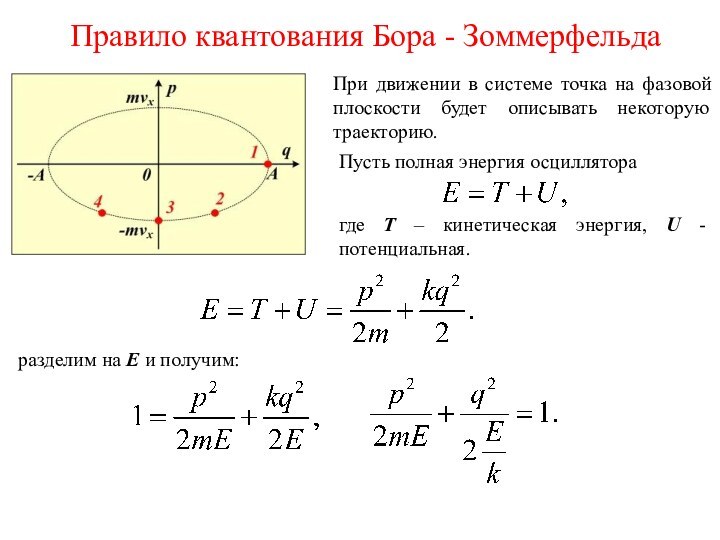
Введём обозначения q = x и mv = p. Каждое состояние линейного осциллятора теперь можно изобразить точкой на фазовой плоскости (как это делалось при подсчёте числа стоячих волн). Каждой точке на фазовой плоскости соответствует своё значение координаты и импульса осциллятора.

будет описывать некоторую траекторию.
Правило квантования Бора - Зоммерфельда
Пусть

где T – кинетическая энергия, U - потенциальная.

разделим на E и получим:

это уравнение эллипса с полуосями
Фазовая траектория линейного осциллятора

Площадь эллипса равна

По определению, величина

и есть действие для осциллятора.

колебаний квантуется, то есть
Здесь T – период колебаний

Правило квантования Бора - Зоммерфельда

получаем, что

осциллятора точка на фазовой плоскости будет описывать эллиптическую траекторию.

Бор стал рассматривать это условие, как общее для всех видов движений с одной степенью свободы (к таким движениям относится и движение электрона в атоме). Возможны только такие фазовые траектории, для которых действие равно nh. Под координатами q и p следует понимать так называемые обобщённые координаты и обобщённые импульсы.

При рассмотрении движения электрона в атоме в качестве координаты удобно выбрать полярный угол φ. В этом случае обобщённым импульсом будет величина pφ = mVr = mr2ω, ω – угловая скорость электрона при движении по орбите. (Легко убедиться, что размерность произведения pφ∙q будет [Дж·с].)

выведенное для линейного осциллятора к движению электрона в атоме

В процессе движения электрона по круговой орбите угловая скорость ω постоянна.

следовательно,

Угол φ меняется в процессе движения от 0 до 2π поэтому,

- орбитальный момент импульса электрона.

круговых орбит: из всех возможных согласно классической механике орбит

Применение правила квантования Бора – Зоммерфельда состоит в следующем:

1. Движение системы описывается при помощи классической механики.

2. Определяются обобщённые координаты и импульс, вычисляется действие системы.

3. Применяется условие, что действие должно быть кратно постоянной Планка.

4. С использованием последнего условия отбираются возможные состояния системы.

ядра по круговой орбите. На него действует кулоновская сила

Необходимо найти полную энергию электрона, учитывая, то значение его момента импульса может изменяться дискретно, то есть

Полная механическая энергия электрона есть сумма его кинетической и потенциальной энергии

Потенциальная энергия электрона в кулоновском поле ядра

орбиты.
здесь Z - заряд ядра.
Запишем второй закон Ньютона. Центростремительное

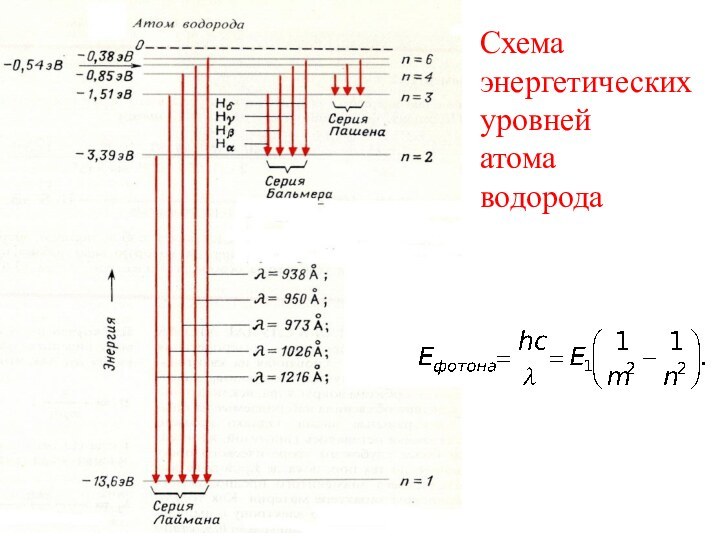
Боровская теория водородоподобного атома

согласно классической механике орбит реализуются только те, у которых

Боровская теория водородоподобного атома

Отсюда

Как было показано ранее

Подставим сюда выражение для скорости V:

откуда

Подставим выражение для радиуса орбиты R в формулу для энергии электрона:

атоме может принимать ряд дискретных значений
При этом, согласно

Здесь n – целое число.

Состояние атома с наименьшей энергией (что соответствует n = 1) называется основным состоянием. Энергия основного состояния

Энергию произвольного состояния с любым номером n удобно выражать через энергию основного состояния:

удобно выражать через радиус первой бороской орбиты:
Боровская теория водородородоподобного

Для атома водорода (Z = 1)

дискретных устойчивых состояниях, характеризуемых определенными дискретными значениями энергии. В

электроны — вопреки классической электродинамике — не излучают электромагнитных

происходит “скачками”, каждый из которых представляет собой порцию (квант

орбиты на внешнюю, более далекую от ядра. При обратном

Бора
Для водорда s = 1, p = 1.
R -

Формула Бальмера - странная, но красивая

м-1.

1913 г.
Стеклянная колба заполнена парами ртути.
Электроны вылетают

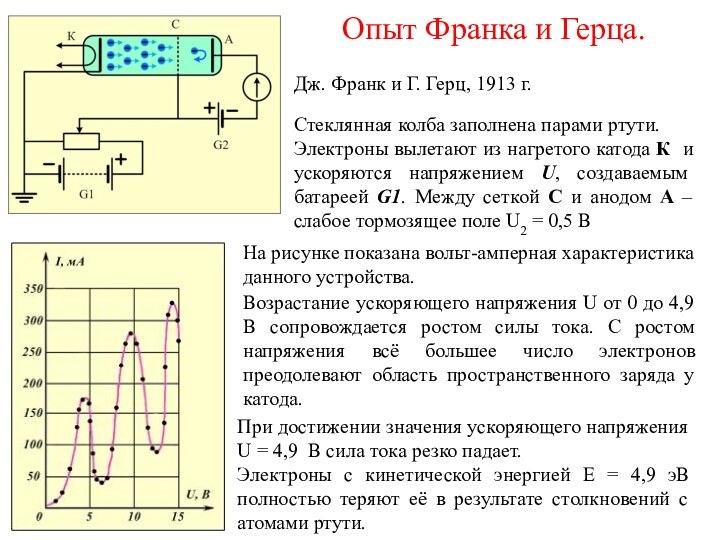
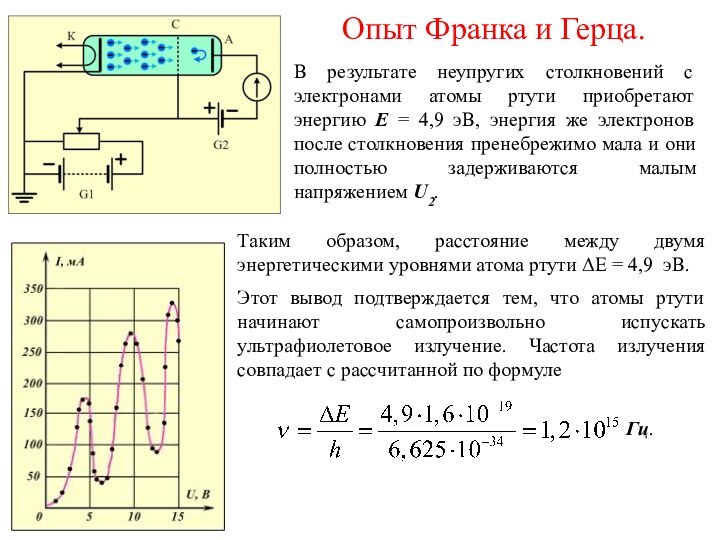
На рисунке показана вольт-амперная характеристика данного устройства.

Возрастание ускоряющего напряжения U от 0 до 4,9 В сопровождается ростом силы тока. С ростом напряжения всё большее число электронов преодолевают область пространственного заряда у катода.

При достижении значения ускоряющего напряжения U = 4,9 В сила тока резко падает.
Электроны с кинетической энергией E = 4,9 эВ полностью теряют её в результате столкновений с атомами ртути.