Слайд 2
4.1 Блок-схема машин. Понятие детали и сборочной единицы.
МП.
Каждая машина обычно состоит из трех частей:
двигатель,
передаточный
механизм (или передача),
исполнительный механизм.
Передаточный механизм необходим для согласования режима работы двигателя с режимом работы исполнительного механизма (обычно, уменьшение частоты вращения, увеличение вращающего момента).
Слайд 3
Механическими передачами, или просто передачами называют механизмы, передающие
работу двигателя испол-нительному органу машины. Передавая механическую энергию, передачи
одновременно могут выполнять следующие функции:
понижать (редукторы) и повышать (мультипликаторы) угловые скорости, соответственно повышая или понижая вращающие моменты;
преобразовывать один вид движения в другой (вращательное в возвратно-поступательное, равномерное в прерывистое и т.д.);
регулировать угловые скорости рабочего органа машины;
реверсировать движение (прямой и обратный ход);
распределять работу двигателя между несколькими исполнительными органами машины.
Передаточное отношение - отношение частот вращения валов в направлении силового потока.
Слайд 4
4.1.2 Классификация передач механической энергии.
В зависимости от принципа
действия все передачи делятся на две группы:
передачи трением –
фрикционные и ременные;
передачи зацеплением – зубчатые, червячные, цепные.
Все передачи трением имеют повышенный износ рабочих поверхностей, так как в них неизбежно проскальзывание одного звена относительно другого.
В зависимости от способа соединения ведущего и ведомого звеньев бывают:
передачи непосредственного контакта – фрикционные зубчатые, червячные;
передачи гибкой связью – ременные, цепные.
Передачи гибкой связью допускают значительные расстояния между ведущим и ведомым валами.
Слайд 6
Основные силовые и кинематические соотношения в передачах
Выбор типа
передачи и ее применение определяется следующими основным характеристиками:
мощностью на
ведущем W1 и ведомом W2 валах;
угловой скоростью ведущего ω 1 и ведомого ω2 валов (рисунок 4.1).
Это две основные характеристики, необходимые для выполнения проектного расчета любой передачи.
Слайд 7
Рассмотрим некоторые кинематические и силовые соотношения на примере
двухступенчатого редуктора (типа привода тигельных машин)
В двухступенча-той передаче с
приводом от электродвигателя (рисунок 4.2) при частоте враще-ния двигателя n1 вал 2 имеет частоту враще-ния n2, а вал 3 – n3. Передаточ-ным отношением ступени i называ-ют отношение угловых скоростей валов 1 и 2.
Слайд 8
(1)
Передаточное отношение ступени i :
Тогда
развиваемый электродвигателем крутящий
момент при мощности W1 и угловой скорости вращения ω1
(2)
или
(3)
где
T1 – в Н·мм; W1 – в Вт; ω1 – в с-1; n – в мин-1.
Коэффициент полезного действия ступени определяют отношением мощности на валах 1 и 2
(4)
Слайд 9
Тогда мощности на валах 2 и 3
(5)
При
известном крутящем моменте на валу 1 T1 крутящие моменты 2 и 3
(6)
Привод с крутящим моментом T3 и частотой вращения n3 может быть использован при соединении вала 3:
с валом с помощью муфты для вращательного движения;
с валом кривошипно-кулисного механизма для поворота ведомого вала на необходимый угол;
с винтом для поступательного перемещения гайки со столом на определенную длину l.
Слайд 10
При использовании в приводе кулачковых, мальтистских, рычажных, стержневых
механизмов можно получать различные законы движения исполнительного механизма.
Зависимость
между развиваемым двигателем крутящим моментом Tдв и противодействующими моментами определяется основным уравнением движения механизма:
(7)
где Iп – момент инерции механизма, приведенный к валу электродвигателя;
ὠ – угловая скорость вращения электродвигателя;
Tc – момент сил сопротивления исполнительного механизма, приведенный к валу электродвигателя;
φ – угол поворота звена приведения (вала электродвигателя).
Слайд 11
В уравнении величину
называют динамическим моментом.
В случае, когда момент инерции механизма не изменяется с углом поворота φ, .
Тогда уравнение (7) принимает вид
(8)
При определении динамического момента
- угловое ускорение звена приведения,
рассчитывают при исследовании переходного процесса работы механизма, который типичен для моментов разгона, останова и реверса.
При работе привода в режиме длительной постоянной или незначительно меняющейся нагрузки
(9)
Слайд 12
Расчеты показывают, что при передаточных отношениях редуктора
приведенный к валу электродвигателя момент инерции
Iп мало отличается от момента инерции ротора Iр. При расчетах принимают
(10)
где Iм – момент инерции приводимого в движение механизма.
В теории электропривода при определении момента инерции ротора электродвигателя используют связь между его величиной и маховым моментом, обозначаемым в каталогах через :
(11)
где M – масса ротора; R – радиус инерции, G – вес тела, Н.
Слайд 13
Приближенно моменты инерции звеньев можно вычислить, если звенья
условно расчленить на отдельные цилиндры. Тогда искомые моменты инерции
определяют как сумму моментов инерции составляющих цилиндров.
Для сплошного цилиндра массой М, диаметром d момент инерции относительно продольной оси
При известной плотности ρ и длине l момент инерции цилиндра
(12)
Слайд 14
4.2 Зубчатые передачи
4.2.1 Общие сведения и классификация зубчатых
передач
Механизм, в котором два подвижных звена являются зубчатыми колесами,
образующими с неподвижным звеном вращательную или поступательную пару, называют зубчатой передачей (рис. 4.3).
Меньшее из колес передачи принято называть шестерней, а большее – колесом, звено зубчатой передачи, совершающее прямолинейное движение, называют зубчатой рейкой (рис. 4.3, г).
При одинаковых размерах колес шестерней называют ведущее зубчатое колесо. Параметры шестерни сопровождаются индексом “1”, а колеса – “2”.
Слайд 15
Рис. 4.3 - Виды зубчатых передач: а, б,
в — цилиндрические зубчатые передачи с внешним зацеплением; г
— реечная передача; д — цилиндрическая передача с внутренним зацеплением; е — зубчатая винтовая передача; ж, з, и — конические зубчатые передачи; к — гипоидная передача
Слайд 16
Зубчатые передачи и колеса классифицируют по следующим признакам (см.

рис. 4.3):
- по взаимному расположению осей колес: с параллельными
осями (цилиндрические, см. рис. 4.3, а—д), с пересекающимися осями (конические, см. рис. 4.3, ж—и), со скрещивающимися осями (винтовые, см. рис. 4.3, е, гипоидные, см.рис. 4.3,к), с преобразованием движения (реечные, см. рис. 4.3, г);
- по расположению зубьев относительно образующих колес: прямозубые (продольная ось зуба параллельна образующей поверхности колеса (рис. 4.3, а)); косозубые (продольная ось зуба направлена под углом к образующей поверхности колеса (рис. 4.3, б)); шевронные (зуб выполнен в форме двух косозубых колес со встречным наклоном осей зубьев (рис. 4.3, в)); с круговым зубом (ось зуба выполнена по окружности относительно образующей поверхности колеса);
- по направлению косые зубья бывают правые и левые.
- шевронные колеса по виду шеврона бывают с непрерывным шевроном (см. рис. 4.3,в) и имеющие между полушевронами канавку для выхода режущего инструмента.
- по конструктивному оформлению: открытые (бескорпусные) и закрытые (корпусные). Конструктивно зубчатые передачи большей частью выполняют закрытыми в общем жестком и герметичном корпусе, что обеспечивает им высокую точность сборки и защиту от загрязнения.
Слайд 17
- по окружной скорости: тихоходные (до 3 м/с),

для средних скоростей (3—15 м/с), быстроходные (св. 15 м/с);
-
по числу ступеней: одно- и многоступенчатые;
- по расположению зубьев в передаче и колесах: внешнее (зубья направлены своими вершинами от оси вращения колеса (см. рис. 4.3, а, б, в)), внутреннее (зубья одного из зацепляющихся колес направлены своими вершинами к оси вращения колеса (см. рис. 4.3, д)) и реечное зацепление (одно из колес заменено прямолинейной зубчатой рейкой (см. рис. 4.3, г));
- по форме профиля зуба: эвольвентные - рабочий профиль зуба очерчен по эвольвенте круга (линия описываемая точкой прямой, катящейся без скольжения по окружности); циклоидальные - рабочий профиль зуба очерчен по круговой циклоиде (линия описываемая точкой окружности, катящейся без скольжения по другой окружности); цевочное (разновидность циклоидального) – зубья одного из колес, входящих в зацепление, заменены цилиндрическими пальцами – цевками; с круговым профилем зуба (зацепление Новикова) – рабочие профили зубьев образованы дугами окружности практически одинаковых радиусов.
- по относительной подвижности геометрических осей зубчатых колес: с неподвижными осями колес - рядовые передачи; с подвижными осями некоторых колес - планетарные передачи.
- по жесткости зубчатого венца колес, входящих в зацепление: с колесами неизменяемой формы (с жестким венцом); включающая колеса с венцом изменяющейся формы (гибким).
Слайд 18
- по величине передаточного числа:
с передаточным числом u ≥ 1
– редуцирующие (редукторы - большинство зубчатых передач);
с передаточным
числом u < 1 – мультиплицирующие (мультипликаторы).
Реализуемое передаточное число может быть постоянным и ступенчато-регулируемым осевым перемещением колес по валу (в коробках скоростей).
-. по точности зацепления
Стандартом предусмотрено 12 степеней точности. Практически передачи общего машиностроения изготовляют от шестой до десятой степени точности. Передачи, изготовленные по шестой степени точности, используют для наиболее ответственных случаев.
- по назначению различают:
силовые передачи, предназначенные для передачи мощности;
кинематические передачи, то есть передачи, не передающие значительной мощности, а выполняющие чисто кинематические функции.
Слайд 19
4.2.2 Достоинства и недостатки зубчатых передач
Основные достоинства зубчатых

передач по сравнению с другими передачами:
- технологичность, постоянство передаточного числа;
-
высокая нагрузочная способность (до N=50000 кВт);
- высокий КПД (до 0,97-0,99 для одной пары колес);
- малые габаритные размеры по сравнению с другими видами передач при равных условиях;
- большая надежность в работе, простота обслуживания;
- сравнительно малые нагрузки на валы и опоры.
К недостаткам зубчатых передач следует отнести:
- невозможность бесступенчатого изменения передаточного числа;
- высокие требования к точности изготовления и монтажа;
- шум при больших скоростях; плохие амортизирующие свойства;
- громоздкость при больших расстояниях между осями ведущего и ве домого валов;
- потребность в специальном оборудовании и инструменте для нарезания зубьев;
- высокая жесткость, не позволяющая компенсировать динамические нагрузки;
- нерациональное использование зубьев – в работе передачи одновременно участвуют обычно не более двух зубьев каждого из зацепляющихся колёс;
- зубчатая передача не предохраняет машину от возможных опасных перегрузок.
Слайд 20
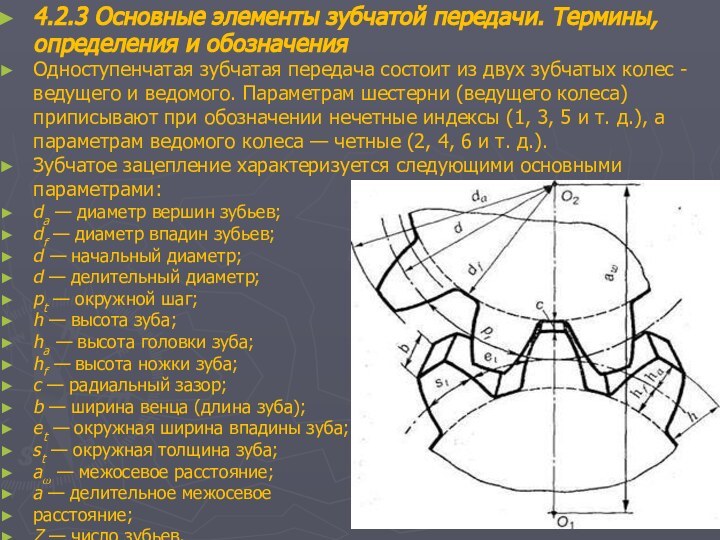
4.2.3 Основные элементы зубчатой передачи. Термины, определения и
обозначения
Одноступенчатая зубчатая передача состоит из двух зубчатых колес -
ведущего и ведомого. Параметрам шестерни (ведущего колеса) приписывают при обозначении нечетные индексы (1, 3, 5 и т. д.), а параметрам ведомого колеса — четные (2, 4, 6 и т. д.).
Зубчатое зацепление характеризуется следующими основными параметрами:
da — диаметр вершин зубьев;
df — диаметр впадин зубьев;
d — начальный диаметр;
d — делительный диаметр;
рt — окружной шаг;
h — высота зуба;
ha — высота головки зуба;
hf — высота ножки зуба;
с — радиальный зазор;
b — ширина венца (длина зуба);
еt — окружная ширина впадины зуба;
st — окружная толщина зуба;
a? — межосевое расстояние;
а — делительное межосевое
расстояние;
Z — число зубьев.
Слайд 21
Делительная окружность - окружность, по которой обкатывается инструмент
при нарезании. Делительная окружность связана с колесом и делит
зуб на головку и ножку.
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.
Линейную величину, в ? раз меньшую окружного шага зубьев, называют окружным модулем зубьев и обозначают т :
Размеры цилиндрических прямозубых колес вычисляют по окружному модулю, который называют расчетным модулем зубчатого колеса, или просто модулем; обозначают буквой т . Модуль измеряют в миллиметрах. Модули стандартизованы.
Слайд 22
Начальная окружность — каждая из взаимокасающихся окружностей зубчатых
колес передачи, принадлежащая начальной поверхности данного зубчатого колеса.
Начальные окружности
являются сопряженными, т.е. это понятие относится к паре колес, находящихся в зацеплении (к передаче). При изменении межосевого расстояния aω начальные диаметры тоже соответственно изменяются, так как aω равно сумме радиусов этих окружностей. Таким образом, у пары колес, находящихся в зацеплении, может быть сколько угодно начальных окружностей, в то время как для отдельно взятого зубчатого колеса понятие начальной окружности вообще лишено смысла.
По делительному диаметру d окружные шаги соответствуют стандартному модулю т. Для цилиндрических прямозубых колес, например, или d = mz.
Основными называются окружности, по которым развер-тываются эвольвенты, очерчивающие профили зубьев.
Слайд 23
Окружностями выступов и впадин называются окружности, ограничивающие вершины и
впадины зубьев.
Линией зацепления называется геометрическое место точек контакта зубьев в
зацеплении. В эвольвентном зацеплении линия зацепления - прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям.
Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров.
Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса.
Для определения основных параметров зубчатой передачи принимают делительный радиус. Если межосевое расстояние в передаче равно сумме делительных радиусов, то начальные и делительные окружности в этом случае совпадают. В дальнейшем рассматривается именно такой частный случай зацепления.
Слайд 24
Высота зуба h — радиальное расстояние между окружностями
вершин и впадин зубчатого колеса:
H = ha + hf.
Головка
зуба — его часть, расположенная между делительной окружностью цилиндрического зубчатого колеса и окружностью вершин зубьев; ha — высота головки зуба.
Ножка зуба — часть зуба, расположенная между делительной окружностью и окружностью впадин (высота ножки зуба - hf ).
Радиальный зазор — расстояние между поверхностями вершин зубьев и впадин шестерни и колеса:
с = hf - ha.
Окружная толщина зуба st — расстояние между разноименными профилями зуба по дуге концентрической окружности зубчатого колеса.
Слайд 25
Ширина венца b — наибольшее расстояние между торцами
зубьев цилиндрического зубчатого колеса по линии, параллельной его оси.
Межосевое
расстояние aω — расстояние между осями зубчатых колес передачи.
Основную теорему зацепления можно сформулировать так: общая нормаль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние на отрезки, обратно пропорционально угловым скоростям.
В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN.
Эту прямую называют линией зацепления.
Длина линии зацепления qa — отрезок линии зацепления, отсекаемый окружностями вершин зубьев сопряженных колес. Он определяет начало и конец зацепления пары сопряженных зубьев. Длина зацепления — активная часть линии зацепления.
В процессе работы сопряженных (эвольвентных) профилей точка их касания все время
Слайд 26
4.2.4 Цилиндрические прямозубые передачи. Устройство и основные геометрические
соотношения
Зубчатую передачу с параллельными осями, у колес которой поверхности
по диаметру выступов цилиндрические, называют цилиндрической.
Цилиндрическая прямозубая зубчатая передача состоит из двух или нескольких пар цилиндрических зубчатых колес с прямыми зубьями (рис.4.4).
Эта передача наиболее проста в изготовлении.
Применяется как в открытом, так и в закрытом исполнении.
Слайд 27
Рис. 4.4 - Цилиндрическая прямозубая передача
Слайд 28
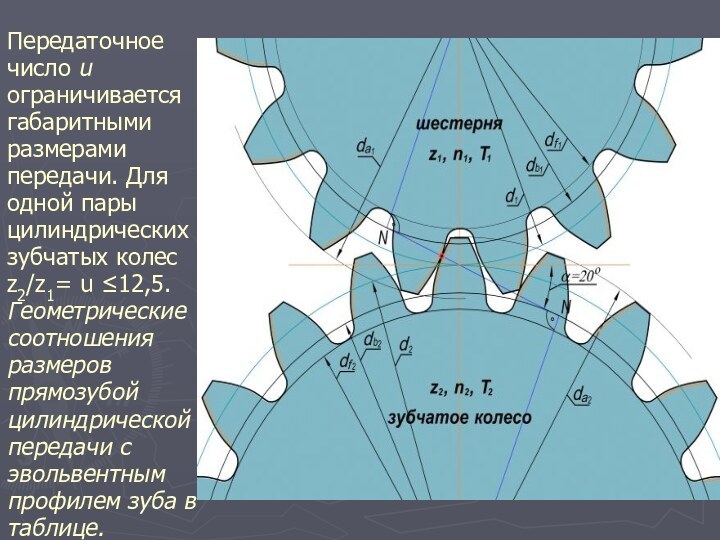
Передаточное число u ограничивается габаритными размерами передачи. Для
одной пары цилиндрических зубчатых колес z2/z1= u ≤12,5.
Геометрические
соотношения
размеров
прямозубой
цилиндрической передачи с
эвольвентным
профилем зуба в таблице.
Слайд 31
Кинематические параметры зубчатых передач − это угловые скорости

ω1 и ω2, частоты вращения n1, n2 ведущего и
ведомого зубчатых колес и передаточное число u зубчатой передачи, вычисляемое по соотношению
(4.5)
Учитывая вышеизложенное, нетрудно установить, что
(4.6)
Для нормальной работы зубчатой передачи (обеспечение плавности работы, отсутствие излишних вибраций и инерционных сил, относительно высокий КПД зубчатого зацепления) форма рабочей поверхности профиля зубьев должна удовлетворять следующим требованиям:
1) в течение времени взаимодействия рабочих поверхностей двух сопряженных зубьев ведущего и ведомого колес передаточное отношение должно сохраняться постоянным (основная теорема зубчатого зацепления);
2) профиль зуба должен обеспечивать выполнение условия 1 при зацеплении данного колеса с любым другим колесом того же модуля;
3) профиль зуба должен обеспечивать возможность изготовления колеса любого диаметра одним инструментом;
4) инструмент для нарезания зубьев должен быть простым и легко доступным для изготовления и контроля.
Слайд 32
Схема расчета зубьев на изгиб
На рис. показан профиль
балки равного сопротивления (s — толщина зуба в опасном сечении; l — плечо изгибающей
силы; b ω— длина зуба; Fn — нормальная сила, действующая на зуб). Определим силы в опасном сечении корня зуба. Разложим силу Fn в точке А на две составляющие: Ft и Fr, условно принимаем, что сила Fn приложена только к одному зубу (перекрытием пренебрегаем), а сила Ft равна окружной силе на начальной окружности.
Слайд 33
При выводе формул принимают следующие упрощения и допущения:
зуб рассматривают как
консольную балку прямоугольного сечения, работающую на изгиб и сжатие;
вся нагрузка, действующая в зацеплении, передается одной парой зубьев и приложена к их вершинам;
нагрузка равномерно распределена по длине зуба .
Слайд 34
Сила Ft изгибает зуб, а сила Fr сжимает
его. Находим:
Ft =Fncos α; Fr =Fnsin α
где α — угол
направления нормальной силы Fn, приложен-ной у вершины, который несколько больше угла зацепле-ния ; Fn =Ft/cos — нормальная сила.
Исходя из изложенного выше, за расчетное напряжение принимают напряжения на растянутой стороне зуба:
(1)
Для опасного сечения ВС условие прочности:
где σF — напряжение изгиба в опасном сечении корня зуба; W — осевой момент сопротивления; A= s b ω — площадь сечения ножки зуба.
Выразим I и s в долях модуля зубьев: l= km; s = cm,
где к и с — коэффициенты, зависящие от формы зуба, т.е. от угла и числа зубьев Z.
Тогда изгибающий момент в опасном сечении
MB=Ft∙l=Ft∙km;
Слайд 35
осевой момент сопротивления прямоугольного сечения зуба
Подставим в формулу
(2) входящие в него параметры МИ и W, введем коэффициенты расчетной нагрузки (табл.
6), KFV (табл. 7) и теоретический коэффициент концентрации напряжений КТ.
В результате получим окончательную формулу проверочного расчета прямозубой передачи на усталость при изгибе
где YF — коэффициент учитывающий форму зуба и концентрацию напряжений.
Слайд 36
Выведем формулу проверочного расчета прямозубых передач на усталость
при изгибе через вращающий момент Т2..
С учетом того, что
Ft=2T1/d1=2T1/mz1=2T2/mz1u;
= mz1
формула проверочного расчета (4) примет вид
где , , МПа; m, мм; T2 — вращающий момент на колесе, Нмм; Z1 — число зубьев шестерни; ψ bd — коэффициент длины зуба (ширины венца) по делительному диаметру.
Из формул (5) и (6) получаем формулы
проектировочного расчета на изгиб P1=T1
где Km = 1,4 для прямозубых колес.
Слайд 37
4.2.5 Расчет цилиндрической прямозубой передачи на контактную прочность
Расчет

прочности контактирующих поверхностей зубьев основан на ограничении наибольших нормальных
напряжений.
При выводе формул приняты следующие допущения: зубья рас-сматривают как два находящихся в контакте цилиндра с параллель-ными образующими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно распределенной по длине зуба; контактирующие профили предполагают неразделенными масляной пленкой.
На основании этих допущений к расчету зубчатых колес можно применить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:
(4.5)
Где q — расчетная удельная нормальная нагрузка;
пр — приведенный модуль упругости материалов зубьев;
ρпр — приведенный радиус кривизны профилей зубьев шестерни и колеса;
μ — коэффициент Пуассона.
Слайд 38
Для прямозубых колес без учета коэффициентов нагрузки
,
(17)(4.6)
где — нормальная сила, действующая на зуб (см. рис. 4.9); Ft — окружная сила;
— суммарная длина контактной линии (для прямозубых передач;
— ширина венца, так как ;
здесь — коэффициент, учитывающий непостоянство суммарной длины контактной линии); — коэффициент перекрытия.
Для учета неравномерности распределения нагрузки по длине контактных линий, а также для учета динамических нагрузок вследствие погрешности изготовления и деформации деталей передачи вводят коэффициент нагрузки .
Отсюда (4.7)
Слайд 39
Приведенный модуль упругости Епр=2Е1Е2/(Е1+Е2), где E1 и E2 — модули упругости материалов шестерни
и колеса.
Зубья рассматриваются как цилиндры длиной ba (ширина зубчатого колеса) и
радиусов ρ1 и ρ2 , где
Приведенный радиус кривизны зубьев в полюсе
Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внутреннего зацепления.
Подставляя значения ρпр и q в формулу (4.6), после преобразований получим (4.8)
Слайд 40
Обозначим в формуле (4.8) выражение
через ZH —
коэффициент, учитывающий форму сопряженных поверхностей зубьев;
— коэффициент, учитывающий
механические свойства материалов сопряженных колес (ZM= 275 МПа1/2 — для стальных колес);
— коэффициент, учитывающий суммарную длину контактных линии для (
прямозубых передач).
Получим расчетную формулу, рекомендуемую для проверочного расчета:
(4.9)
Слайд 41
После подстановки значений Ft=2T2/d1u; d1=2
И
в формулу (4.9)
и некоторых преобразований получим удобную для расчета формулу(4.10)
Значение ψba
определяют по формуле
После некоторых преобразований формулы (4.10) получим формулу проектировочного расчета для определения межосевого расстояния прямозубых зубчатых передач:
Обозначим через вспомогательный коэффициент Ka (для прямозубых передач при KHV= 1,25, Ka= 49,5 МПа1/3).
Слайд 42
Допускаемые контактные напряжения (МПа) при расчете рабочих поверхностей
на усталостное выкрашивание рассчитываются по формуле
,
Где — предел выносливости рабочих поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений NHlim, МПа (база испытаний NH0 определяется по табл.);
SH — коэффициент безопасности (SH= 1,1 при нормализации, улучшении или объемной закалке; при поверхностной закалке и цементации SH=1,2); ZR — коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев (ZR=1 0,9);
KHL — коэффициент долговечности, который учитывает влияние срока службы, режима нагрузки передачи и возможность повышения допускаемых напряжений для кратковременно работающих передач.
Слайд 43
При постоянной нагрузке
;
(или ) — циклическая долговечность.
При переменной нагрузке расчетная циклическая долговечность определяется по формуле:
,
где КНЕ — коэффициент приведения переменного режима нагружения к постоянному эквивалентному
В расчетные формулы (4.10) и (4.11) входит меньшее из допускаемых напряжений, установленных для шестерни и колеса. Так как материал колеса имеет обычно меньшую твердость, чем материал шестерни, то в большинстве случаев для колеса меньше.
Слайд 44
4.2.7 Последовательность проектировочного расчета цилиндрической прямозубой передачи
1. Определить

передаточное число u.
2. В зависимости от условий работы передачи выбрать
материалы колес, назначить термическую обработку и значения твердости рабочих поверхностей зубьев (табл. 13).
3. Определить базу испытаний NHO, расчетную циклическую долговечность NH, вычислить коэффициенты и допускаемые напряжения изгиба.
4. Выбрать коэффициент длины зуба (ширины венца колеса) и рассчитать .
5. Определить межосевое расстояние из условия контактной прочности по формуле (22) и округлить его значение до стандартного.
Для стандартных редукторов расчетное значение округляют до ближайшего большего значения: 40, 50, 63, 80, 100, 125, (140), 160, (180), 200, (225), 250, (280), 315, (335), 400, (450), 500, (560), 630, (710), 800, (900), 1000 и т. д. до 25 000 (в скобках значения по 2-му ряду стандарта для aω).
6. Задать модуль из соотношения m=(0,01 0,02) и округлить его значение до ближайшего стандартного (см. табл. 3). При этом в силовых передачах желательно, чтобы модуль был не менее 1,5-2 мм.
Слайд 45
7. Определить суммарное число зубьев , передачи, числа зубьев
шестерни и колеса.
8. По табл. 8 выбрать коэффициенты формы
зубьев YFi и YF2 для шестерни и колеса.
9. Проверить прочность зубьев по напряжениям изгиба. При неудовлетворительных результатах
( )
необходимо путем соответствующего изменения числа зубьев и модуля; при том же межосевом расстоянии добиться уменьшения напряжений изгиба, не нарушая при этом условия контактной прочности.
10. Произвести геометрический расчет передачи.
11. Определить окружную скорость колеса v и по табл. 14 назначить соответствующую степень точности зацепления.
Слайд 46
Передачи с эвольвентным зацеплением.
Наиболее полно перечисленным требованиям
удовлетворяет эвольвентное зацепление, предложенное Леонардом Эйлером (1760 или 65
г.) и широко применяемое в общепромышленной и военной технике.
Основные параметры эвольвентных цилиндрических зубчатых передач стандартизованы.
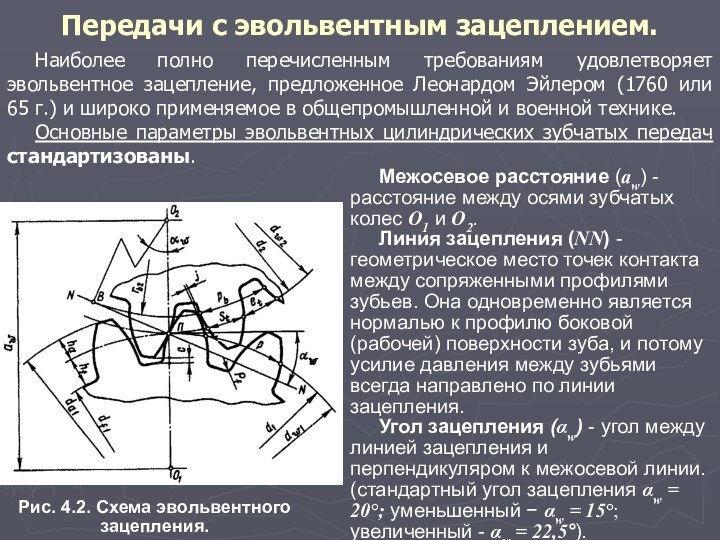
Рис. 4.2. Схема эвольвентного зацепления.
Межосевое расстояние (аw) - расстояние между осями зубчатых колес О1 и О2.
Линия зацепления (NN) - геометрическое место точек контакта между сопряженными профилями зубьев. Она одновременно является нормалью к профилю боковой (рабочей) поверхности зуба, и потому усилие давления между зубьями всегда направлено по линии зацепления.
Угол зацепления (αw) - угол между линией зацепления и перпендикуляром к межосевой линии. (стандартный угол зацепления αw = 20°; уменьшенный − αw = 15°; увеличенный - αw = 22,5°).
Слайд 47
Основные параметры эвольвентных конических зубчатых передач
Конические зубчатые
эвольвентные передачи предназначены для передачи вращательного движения между валами,
геометрические оси которых пересекаются. Наиболее часто угол между осями валов составляет 90°, передачи с таким углом принято называть ортогональными (рис. 4.3).
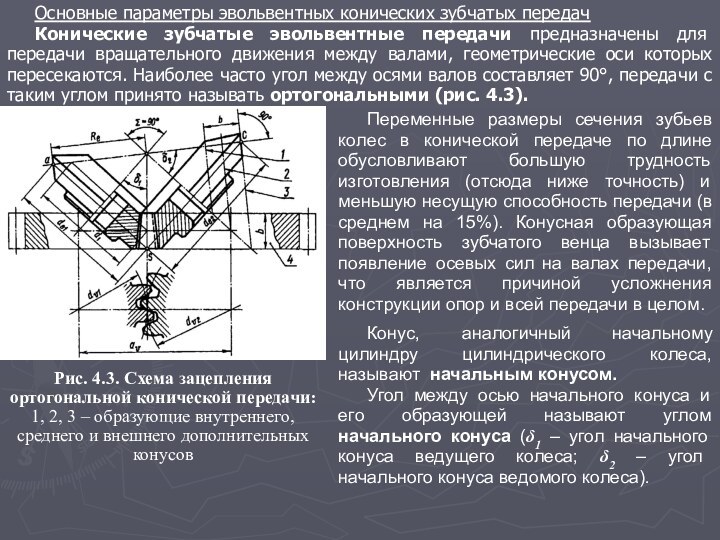
Рис. 4.3. Схема зацепления ортогональной конической передачи: 1, 2, 3 – образующие внутреннего, среднего и внешнего дополнительных конусов
Переменные размеры сечения зубьев колес в конической передаче по длине обусловливают большую трудность изготовления (отсюда ниже точность) и меньшую несущую способность передачи (в среднем на 15%). Конусная образующая поверхность зубчатого венца вызывает появление осевых сил на валах передачи, что является причиной усложнения конструкции опор и всей передачи в целом.
Конус, аналогичный начальному цилиндру цилиндрического колеса, называют начальным конусом.
Угол между осью начального конуса и его образующей называют углом начального конуса (δ1 – угол начального конуса ведущего колеса; δ2 – угол начального конуса ведомого колеса).