Слайд 2
Общие сведения
Зубчатая передача – трехзвенный механизм, включающий два
подвижных звена, взаимодействующих между собой через высшую зубчатую кинематическую
пару и образующих с третьим неподвижным звеном низшие (вращательные или поступательные) кинематические пары (рисунок 1).
Рисунок 1 – Виды зубчатых передач
Меньшее зубчатое колесо называют шестерня, большее –колесо. Звено, движущееся прямолинейно (если оно имеется), называют зубчатой рейкой (рисунок 1, к).
Назначение зубчатой передачи – передача движения (обычно вращательного) с преобразованием параметров, а иногда и его вида (реечная передача). Зубчатые передачи вращательного движения наиболее распространены в технике (рисунок 1, от а до и).
Слайд 3
Достоинства зубчатых передач
1 Высокая надежность работы в
широком диапазоне нагрузок и скоростей.
2 Большой ресурс.
3
Малые габариты.
4 Высокий КПД (до 0,98).
5 Относительно малые нагрузки на валы и подшипники.
6 Постоянство передаточного числа.
7 Простота обслуживания.
Недостатки зубчатых передач
1 Сложность изготовления и ремонта (необходимо высокоточное специализированное оборудование).
2 Относительно высокий уровень шума, особенно на больших скоростях.
3 Нерациональное использование зубьев – в работе передачи одновременно участвуют обычно не более двух зубьев каждого из зацепляющихся колёс.
Слайд 4
Классификация зубчатых передач
1 По величине передаточного числа:
1.1 с
передаточным числом u 1 – редуцирующие (редукторы);
1.2 с
передаточным числом u < 1 – мультиплицирующие (мультипликаторы).
2 По взаимному расположению валов:
2.1 с параллельными валами – цилиндрические (рисунок 1, от а до г);
2.2 с пересекающимися осями валов – конические (конические передачи с углом 90 между осями валов называют ортогональными; рисунок 1, от д до ж);
2.3 с перекрещивающимися осями валов – червячные, винтовые (рисунок 1, и), гипоидные (рисунок 1, з);
2.4 с преобразованием движения – реечные (рисунок 1, к).
3 По расположению зубьев относительно образующей поверхности колеса:
3.1 прямозубые – продольная ось зуба параллельна образующей поверхности колеса (рисунок 1, а, г, д, к);
3.2 косозубые – продольная ось зуба направлена под углом к образующей поверхности колеса (рисунок 1, б, е, и);
Слайд 5
3.3 шевронные – выполненых в форме двух косозубых

колес со встречным наклоном осей зубьев (рисунок 1, в);
3.4
с круговым зубом – ось зуба выполнена по окружности относительно образующей поверхности колеса (рисунок 1, ж, з).
4 По форме зацепляющихся звеньев:
4.1 с внешним зацеплением – зубья направлены своими вершинами от оси вращения колеса (рисунок 1, от а до в);
4.2 с внутренним зацеплением зубья одного из зацепляющихся колес направлены своими вершинами к оси вращения колеса (рисунок 1, г);
4.3 реечное зацепление – одно из колес заменено прямолинейной зубчатой рейкой (рисунок 1, к);
5 По форме рабочего профиля зуба:
5.1 эвольвентные – рабочий профиль зуба очерчен по эвольвенте круга (линия, описываемая точкой прямой, катящейся без скольжения по окружности);
5.2 циклоидальные – рабочий профиль зуба очерчен по круговой циклоиде (линия, описываемая точкой окружности, катящейся без скольжения по другой окружности);
5.3 с круговым профилем зуба (зацепление Новикова) – рабочие профили зубьев образованы дугами окружности практически одинаковых радиусов.
Слайд 6
6 По относительной подвижности геометрических осей зубчатых колес:
6.1
с неподвижными осями колес – рядовые передачи;
6.2 с подвижными
осями некоторых колес – планетарные передачи.
7 По конструктивному исполнению:
7.1 открытые (бескорпусные);
7.2 закрытые (корпусные редукторы).
Слайд 7
Способы изготовления зубчатых колес
В зависимости от материала и
размеров колес, заготовки для них могут быть получены литьем,
ковкой и штамповкой.
Зубья колес изготавливают следующими способами:
а) накатывание (образование зубьев на специальном прокатном стане в результате пластического деформирования нагретой до 1 000…
1 100° заготовки);
б) нарезание:
– метод копирования (прорезание впадин между зубьями дисковой модульной или пальцевой фрезой);
– метод обкатки (воспроизведение зацепления зубчатой пары: одно звено – заготовка, второе – режущий инструмент «рейка»);
в) литье (наименее точный вид изготовления зубчатых колес, обычно требующий дополнительной мехобработки).
Слайд 8
Способы изготовления зубчатых колес
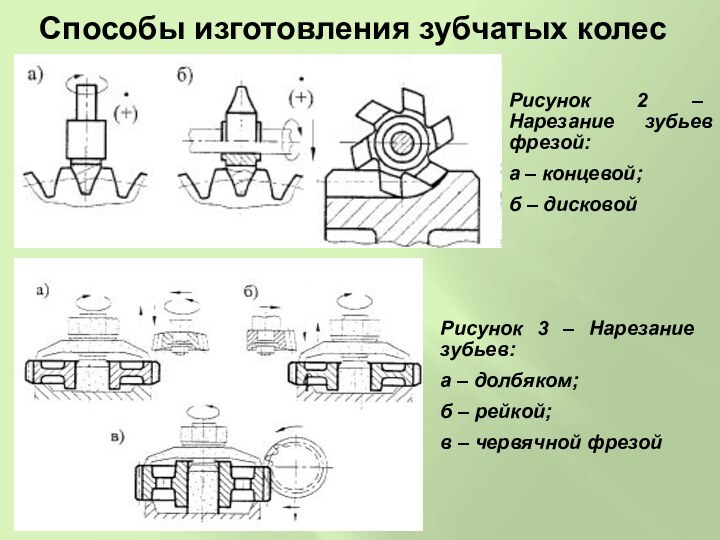
Рисунок 2 – Нарезание зубьев
фрезой:
а – концевой;
б – дисковой
Рисунок 3 – Нарезание зубьев:
а
– долбяком;
б – рейкой;
в – червячной фрезой
Слайд 9
Способы изготовления зубчатых колес
Точность зубчатых колес регламентируется стандартом
(существует 12 степеней точности). Степень точности определяется окружной скоростью
зубчатого колеса.
Для каждой степени точности зубчатого колеса и передачи устанавливаются следующие нормы:
– кинематической точности;
– плавности работы;
– контакта зубьев.
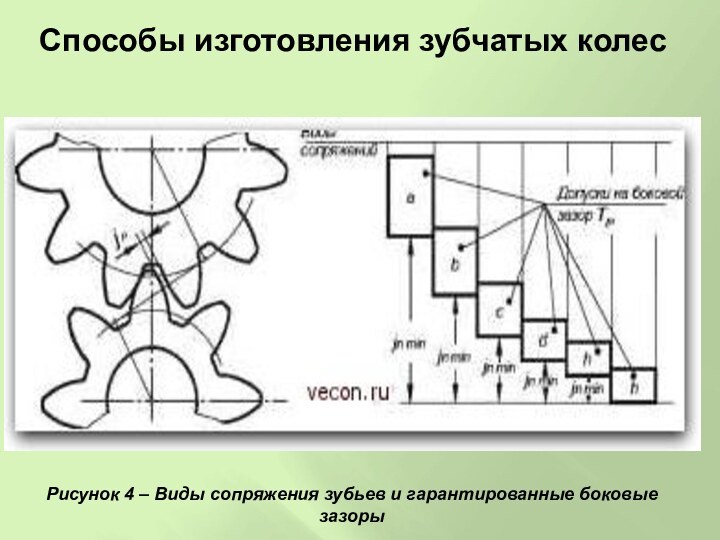
Устанавливается 6 видов сопряжений, имеющих разный гарантированный боковой зазор, исключающий заклинивание:
Н – нулевой зазор; Е – весьма малый зазор;
С, D – уменьшенный зазор; В – нормальный зазор;
А – увеличенный зазор.
Пример обозначения точности колеса: 9-8-7-В ГОСТ 1643-81
Слайд 10
Способы изготовления зубчатых колес
Рисунок 4 – Виды сопряжения
зубьев и гарантированные боковые зазоры
Слайд 11
Основы теории зубчатого зацепления
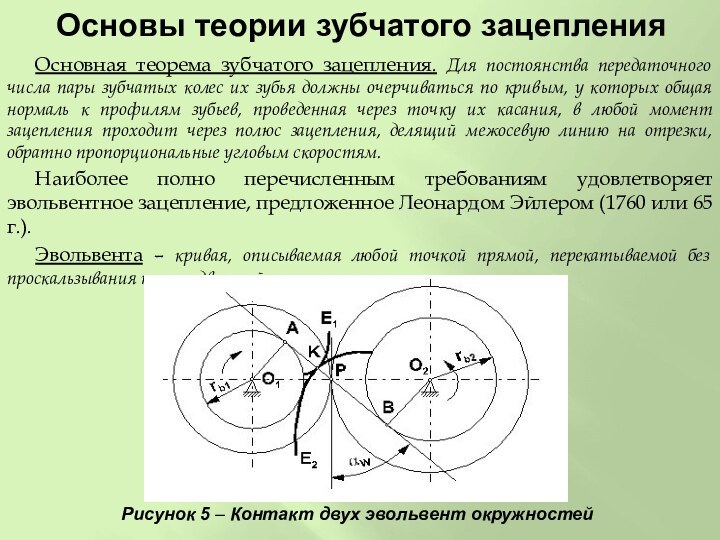
Основная теорема зубчатого зацепления. Для
постоянства передаточного числа пары зубчатых колес их зубья должны
очерчиваться по кривым, у которых общая нормаль к профилям зубьев, проведенная через точку их касания, в любой момент зацепления проходит через полюс зацепления, делящий межосевую линию на отрезки, обратно пропорциональные угловым скоростям.
Наиболее полно перечисленным требованиям удовлетворяет эвольвентное зацепление, предложенное Леонардом Эйлером (1760 или 65 г.).
Эвольвента – кривая, описываемая любой точкой прямой, перекатываемой без проскальзывания по неподвижной окружности.
Рисунок 5 – Контакт двух эвольвент окружностей
Слайд 12
Передачи с эвольвентным зацеплением
Основные параметры эвольвентных цилиндрических зубчатых
передач стандартизованы.
Рисунок 6 – Схема эвольвентного зацепления
Межосевое расстояние
(аw) – расстояние между осями зубчатых колес О1 и О2.
Линия зацепления (NN) – геометрическое место точек контакта между сопряженными профилями зубьев. Она одновременно является нормалью к профилю боковой (рабочей) поверхности зуба, и потому усилие давления между зубьями всегда направлено по линии зацепления.
Нормаль всегда проходит через одну и ту же точку П на линии центров зубчатых колес О1 и О2, называемой полюсом зацепления.
Слайд 13
В полюсе зацепления касаются друг друга две окружности,
перекатывающиеся одна по другой без проскальзывания, и называющиеся начальными
(dw ).
Угол зацепления (w ) – угол между линией зацепления и перпендикуляром к межосевой линии (стандартный угол зацепления w = 20°; уменьшенный w = 15°; увеличенный – w = 22,5°).
Угол наклона зубьев () – угол между продольной осью зуба и образующей поверхности зубчатого венца колеса.
Окружность, являющаяся начальной при зацеплении колеса с рейкой называется делительной (d)
Окружность вершин зубьев (dа ) – окружность, ограничивающая высоту зубьев:
Окружность впадин зубьев (df ) – окружность, ограничивающая глубину впадин:
Передаточное отношение
Слайд 14
Окружной делительный шаг зубьев (p) расстояние между
одноименными боковыми поверхностями двух соседних зубьев, измеренное по дуге
делительной окружности. Так как длина делительной окружности равна d, то для любого зубчатого колеса имеем следующее:
Окружной модуль ( ) – линейная величина в раз меньшая шага, измеренного по делительной окружности.
Модуль является основным параметром зубчатой передачи, определяющим ее размеры. Для пары зацепляющихся колес модуль должен быть одинаковым.
Рисунок 7 – Конструктивные параметры цилиндрических ЗП
Слайд 15
Высота зуба (h) – расстояние между окружностью впадин

и окружностью выступов, измеренное по радиусу, для цилиндрических колес
h = 2,25 m).
Высота головки зуба (hа ) – расстояние между делительной окружностью и окружностью выступов, измеренное по радиусу (обычно hа = m).
Высота ножки зуба (hf ) – расстояние между делительной окружностью и окружностью впадин, измеренное по радиусу (обычно hf = 1,25 m).
Ширина зубчатого венца (b) – расстояние между торцовыми поверхностями зубчатого венца колеса.
Угол поворота колеса от положения входа в зацепление его зуба до выхода из зацепления называется углом перекрытия .
Отношение угла перекрытия зубчатого колеса к его угловому шагу ( ) называется коэффициентом торцевого перекрытия:
Коэффициент торцевого перекрытия показывает сколько пар зубьев в среднем за поворот колеса на один шаг находятся в зацеплении. Для непрерывности зацепления необходимо, чтобы . Коэффициент характеризует плавность зацепления, т.е. с увеличением увеличивается плавность хода и нагрузочная способность передачи, поэтому