Презентация на тему Теоретическая механика

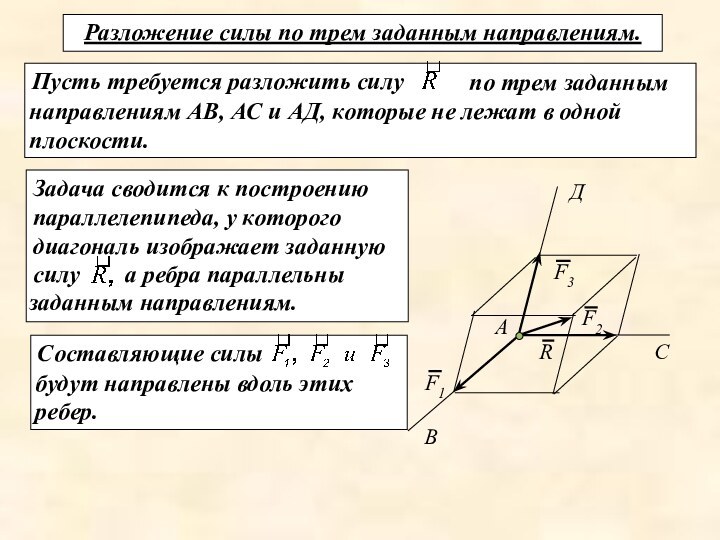
2. Яблонский А.А. Курс теоретической механики. Часть 1.
3.

Задачники
1. Мещерский И.В. Сборник задач по теоретической механике.
2. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в
примерах и задачах. Часть 1.

Статикой называется раздел механики, в котором излагается общее учение

Определение абсолютно твердого тела

Абсолютно твердым телом называется такое тело, расстояние между двумя точками которого всегда остается постоянным.

Тело, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным, а тело, перемещение которого ограничено другими телами – несвободное.

Определение свободного и несвободного тела

мерой механического взаимодействия тел.
Сила - векторная величина. Обозначается:
Параметры,

б) направление силы;

Линия (СД), вдоль которой действует сила, называется линией действия силы.

в) точка приложения силы
(на рисунке – точка А).

единиц (СИ) является 1 ньютон (Н). Более крупная единица

Внешнее и внутренние силы

Опр. Внешними называются силы, которые действуют на тело (на тела системы) со стороны других тел.

Опр. Внутренними называются силы, с которыми части данного тела (тела данной системы) действуют друг на друга.

какой-нибудь одной его точке, называется сосредоточенной.
Распределенные силы
Опр.

Распределенные нагрузки характеризуются интенсивностью q. Размерность [q] = H/м.

q · l, приложенной к середине участка распределения.
Виды

а) равномерно распределенная нагрузка

Действие характеризуется интенсивностью q = const.

Действие характеризуется интенсивностью q(х) = а · х.

Заменяется сосредоточенной силой Q = qmax · l/2, приложенной на расстоянии 1/3 от конца участка распределения, где q = qmax.

Заменяется сосредоточенной силой

Системы сил.

а) совокупность сил, действующих на тело (или тела), называется системой сил;

б) если линии действия всех сил лежат в одной плоскости, то система сил называется плоской, а если не лежат в одной плоскости, - пространственной;

в) системы сил, линии действия которых пересекаются в одной точке, называется сходящимися;

одной точке, называется сходящимися;
г) системы сил, линии действия которых

д) если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными;

е) система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.

то эта сила называется равнодействующей данной системы сил;
б)

Равнодействующая и уравновешивающая силы

сил, действующих на твердое тело, в системы им эквивалентные,

Определение условий равновесия системы сил, действующих на твердое тело.

(аксиомы или принципы) статики

Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F = F / ) и направлены вдоль одной прямой в противоположные стороны.

Аксиома двух сил

Аксиома присоединения

Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

абсолютно твердое тело не изменится, если перенести точку приложения

Аксиома параллелограмма

Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.

А

одного материального тела на другое имеет место такое же

не образуют уравновешенную систему сил, так как приложены к разным телам.

Свойство внутренних сил. Из аксиомы следует, что сумма внутренних сил, действующих на абсолютно твердое тело, образует уравновешенную систему сил, которую можно отбросить. То есть, при изучении условий равновесия тела необходимо учитывать только внешние силы.

Силы

Следствие.

под действием данной системы сил, не нарушится, если тело

Аксиома освобождаемости твердых тел от связей (аксиома связей)

Несвободное твердое тело можно считать свободным, если действие связей заменить их реакциями.

Определение связи
Все то, что ограничивает перемещение тела в

Понятие реакции связи
Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или просто реакцией связи.

Направление реакции связи
Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.

(свободное опирание)
Опр. Гладкой называется поверхность, трением о которую можно

гладкой поверхности или опоры (при свободном опирании) направлена по общей нормали к поверхности соприкасающихся тел в точке их касания и приложена в этой точке.

Вывод. Реакция

дает телу удалиться от точки подвеса нити.

Вывод. Реакция

шарниром) называется связь, которая осуществляет такое соединение тел, при

цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси шарнира.

Вывод. Реакция

или шарнирно-подвижной опорой) называется

шарнирно-подвижной опоры проходит через центр шарнира

Вывод2. Линия действия реакции ползунка проходит центр шарнира перпендикулярно направляющим, в которых движется ползунок.

Вывод1. Линия действия реакции

шарнирно-неподвижная связь, не ограничивающая движение тела вдоль поверхности, по которой связь может перемещаться.

называется связь, которая позволяет соединенным телам как угодно поворачиваться

Вывод1. Реакция сферического шарнира может иметь любое направление в пространстве.

Вывод2. Реакция подпятника может иметь любое направление в пространстве.

по сравнению с воспринимаемой им нагрузкой можно пренебречь.


Вывод. Реакция

называется связь, которая ограничивает любое перемещение тела.

Вывод. Действие

связь, которая ограничивает любое перемещение тела кроме движения по

А

Вывод. Действие скользящей жесткой заделки заменяется наперед неизвестной реакцией, которая направлена перпендикулярно направляющим в плоскости действия сил, и парой сил, с наперед неизвестным моментом МА.

параллелограмма находится по правилу параллелограмма, т.е.
α
А
α
β
γ
Геометрическая сумма двух сил

Модуль R, углы β и γ определятся по формулам.

F1 / sin γ = F2 / sin β = R / sinα.

двух сил

2.1. Сложение сил

Тема 2. Сложение и разложение сил.

плоскости.

трех сил

сил называется геометрическая сумма всех сил, входящих в систему:


Главный

1. Последовательным сложением сил по правилу параллелограмма;

2. С помощью построения многоугольника сил. Каждая сила переносится в масштабе параллельно самой. Последующая сила откладывается от конца предыдущей.

Замыкающая сторона многоугольника – главный вектор

Для системы сходящихся сил главный вектор и равнодействующая совпадают.

направлениям.
Пусть требуется разложить силу


А
D
B
Для этого необходимо построить

направленные по сторонам параллелограмма, будут составляющими силами.

по двум заданным направлениям АВ и АD.

Силы