Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Жидкость

Содержание

2. 1. Упругие напряжения и деформации. Закон Гука
3. Идеально (абсолютно) упругим телом называется такое тело,
4. Выделим бесконечно малый объем вещества в виде
5. Эти величины называются механическими напряжениями.Из второго условия
6. Компоненты
7. Деформация растяжения (сжатия) – характеризуют величиной относительного
8. Деформация сдвига характеризуется величиной относительного сдвигаЗакон ГукаОтносительное
9. Растяжение, например, стержня, сопровождается его поперечным сжатием.
10. Зависимость напряжения от относительного удлинения при растяжении образца Предел упругостиПластическая деформацияДеформационное упрочнениеПредел прочностиТекучее состояние
11. 2. Общие свойства жидкостей и газов
12. Агрегатное состояния веществаТвердое Жидкое ГазообразноеЗависит от соотношения
13. Способы кинематического описания жидкостейСпособ Лагранжа. Выбирается совокупность
14. Линия тока – линия, в каждой точке
15. 3. Поток вектора скорости; уравнение непрерывности
16. Рассмотрим в поле вектора малый плоский элемент
17. Если поверхность имеет конечные размеры S
18. Рассмотрим в поле вектора
19. Если div(v) = 0, в
20. Уравнение непрерывностиВыберем в жидкости объем V, ограничим
21. Уравнение непрерывности жидкости в интегральной форме.Если течение
22. 4. Циркуляция векторного поля. Ротор вектора. Уравнения движения и равновесия жидкости.
23. Пусть в поле скоростей v (x, y,
24. Это локальная характеристика завихренности потока жидкости в окрестности точки А.
25. В жидкости отсутствует понятие сдвига. В жидкости
26. Выберем в жидкости бесконечно малый объем dx, dy,
27. Воспользуемся определением частной производной , т е.
28. Идеальная жидкость – жидкость, вязкостью которой можно
29. Частный случай: несжимаемая жидкость.Жидкость находится в однородном
30. Одно из проявлений закона Паскаля можно наблюдать
31. Вследствие несжимаемости объемы жидкости, перешедшего из одного
32. Согласно формулеСила давления на нижние слои жидкости
33. Поэтому на верхнее основание действует силаНа глубине
34. 6. Стационарное движение идеальной жидкости. Уравнение Бернулли
35. Стационарное течение жидкости - это такое течение,
36. За время dt через сечение
37. При течении жидкости ее отдельные слои текут
38. За время Δt объем жидкости переместится вдоль
39. Изменение полной механической энергииСилы давления на боковую
40. Сечения S1 и S2 были взяты произвольно.
41. 7. Движение тел в среде с сопротивлением. Стационарное течение вязкой жидкости
42. Рассмотрим следующую ситуацию. Пусть у нас имеются
43. Слои жидкости также станут двигаться, причем величина
44. Для величины силы вязкого трения в условиях
45. Вихревая дорожка при обтекании цилиндра
46. Число РейнольдсаЕсли число Рейнольдса мало (Re~1 –
48. 3. Если увеличить число Рейнольдса до (Re~102),
49. Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины «Лос-Анджелес»
51. Скачать презентацию
52. Похожие презентации

1. Упругие напряжения и деформации. Закон Гука

Лекция 10Тема: ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД Упругие напряжения и деформации. Закон Гука.

Идеально (абсолютно) упругим телом называется такое тело, которое обладает свойством восстанавливать свои

Выделим бесконечно малый объем вещества в виде куба. Обозначим dS – площадь боковых

Эти величины называются механическими напряжениями.Из второго условия равновесия суммарный момент, например, сил

Деформация растяжения (сжатия) – характеризуют величиной относительного удлинения.Если выделенный в теле объем

Деформация сдвига характеризуется величиной относительного сдвигаЗакон ГукаОтносительное растяжение (сжатие) ε пропорционально растягивающему

Растяжение, например, стержня, сопровождается его поперечным сжатием. - относительное сжатие. Относительное сжатие связано

Зависимость напряжения от относительного удлинения при растяжении образца Предел упругостиПластическая деформацияДеформационное упрочнениеПредел прочностиТекучее состояние

Агрегатное состояния веществаТвердое Жидкое ГазообразноеЗависит от соотношения между потенциальной энергией взаимодействия атомов

Способы кинематического описания жидкостейСпособ Лагранжа. Выбирается совокупность «жидких» частиц, движение жидкости описывается

Линия тока – линия, в каждой точке которой вектор скорости

3. Поток вектора скорости; уравнение непрерывности

Рассмотрим в поле вектора малый плоский элемент поверхности с площадью dS. Введем

Если поверхность имеет конечные размеры S разбить на плоские малые

Рассмотрим в поле вектора малый объем ΔV, окруженный замкнутой

Если div(v) = 0, в т. А нет источников (стоков).Если

Уравнение непрерывностиВыберем в жидкости объем V, ограничим замкнутой поверхностью S. Поток массы

Уравнение непрерывности жидкости в интегральной форме.Если течение стационарно, т.е. величины, характеризующие течение

4. Циркуляция векторного поля. Ротор вектора. Уравнения движения и равновесия жидкости.

Пусть в поле скоростей v (x, y, z) задана некоторая кривая L.

Это локальная характеристика завихренности потока жидкости в окрестности точки А.

В жидкости отсутствует понятие сдвига. В жидкости могут быть только напряжения всестороннего

Выберем в жидкости бесконечно малый объем dx, dy, dz – длины ребер.

Воспользуемся определением частной производной , т е. проекция силы давления, отнесенная к

Идеальная жидкость – жидкость, вязкостью которой можно пренебречь.Запишем второй закон Ньютона

Частный случай: несжимаемая жидкость.Жидкость находится в однородном поле тяготения.Выберем положительное направление оси

Одно из проявлений закона Паскаля можно наблюдать в гидравлическом прессе: два сообщающихся

Вследствие несжимаемости объемы жидкости, перешедшего из одного цилиндра в другой, одинаковы: Работы, совершаемые

Согласно формулеСила давления на нижние слои жидкости будет больше, чем на верхние.

Поэтому на верхнее основание действует силаНа глубине h + a давление равноПоэтому

6. Стационарное движение идеальной жидкости. Уравнение Бернулли

Стационарное течение жидкости - это такое течение, при котором скорость жидкости в

За время dt через сечение пройдет объем жидкости

При течении жидкости ее отдельные слои текут с разными скоростями, скользят друг

За время Δt объем жидкости переместится вдоль трубки тока. В силу непрерывности

Изменение полной механической энергииСилы давления на боковую поверхность трубки тока перпендикулярны в

Сечения S1 и S2 были взяты произвольно. Поэтому в стационарно текущей идеальной

7. Движение тел в среде с сопротивлением. Стационарное течение вязкой жидкости

Рассмотрим следующую ситуацию. Пусть у нас имеются две большие параллельные пластины, площадью

Слои жидкости также станут двигаться, причем величина скорости этих слоев будет линейно

Для величины силы вязкого трения в условиях рассматриваемого опыта справедливо равенствоФормула Ньютона

Число РейнольдсаЕсли число Рейнольдса мало (Re~1 – 10-2), то течение через некоторое

3. Если увеличить число Рейнольдса до (Re~102), то характер течения снова меняется

Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины «Лос-Анджелес»

Лекция оконченаНажмите клавишу для выхода

Слайды презентации

Слайд 2 1. Упругие напряжения и деформации. Закон Гука

Слайд 3 Идеально (абсолютно) упругим телом называется такое тело, которое

Идеально (абсолютно) упругим телом называется такое тело, которое обладает свойством восстанавливать

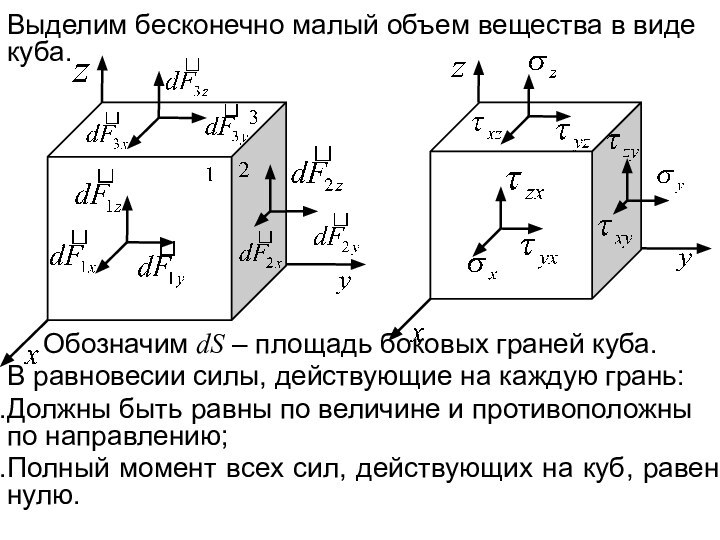
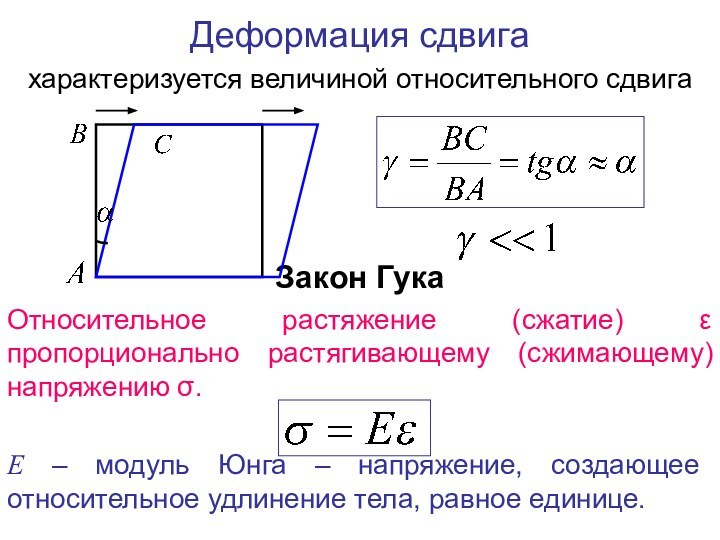
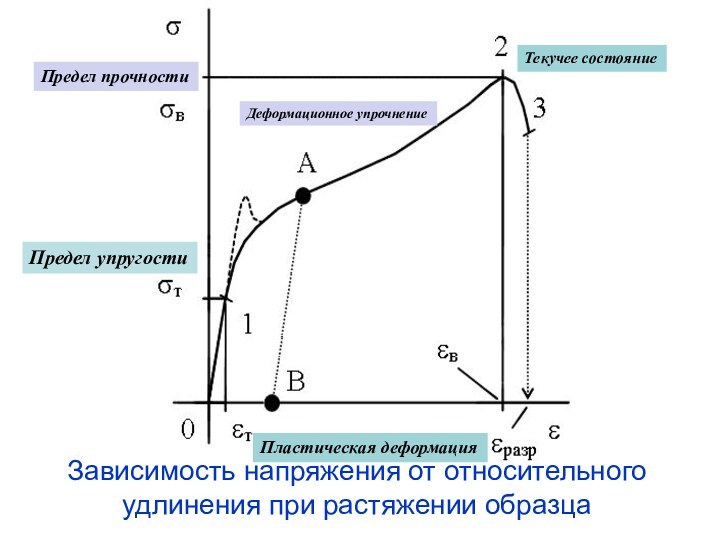
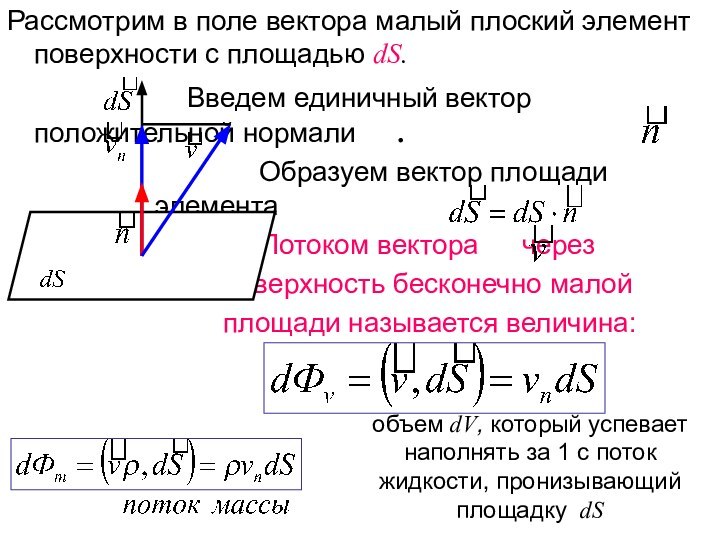
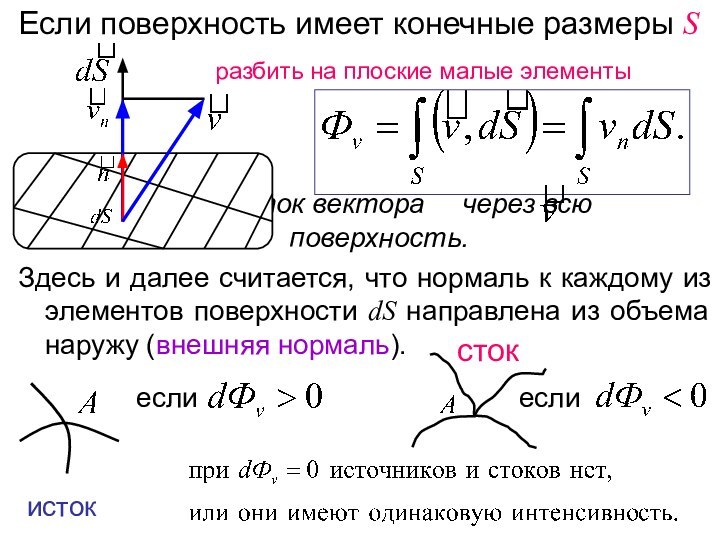
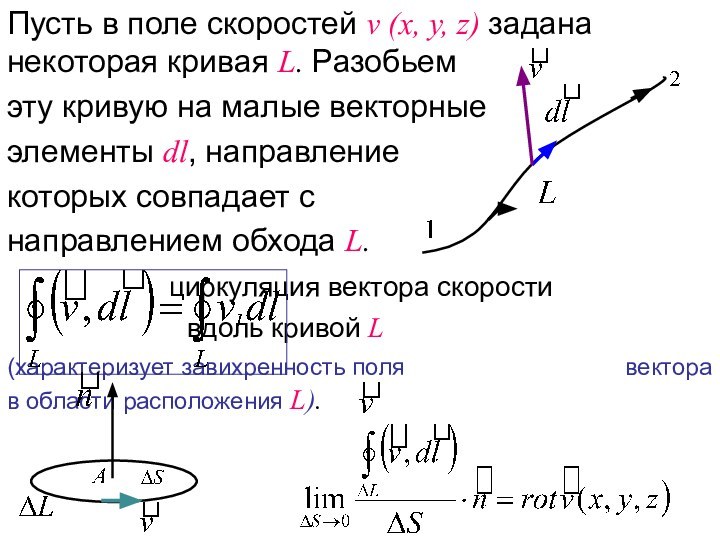
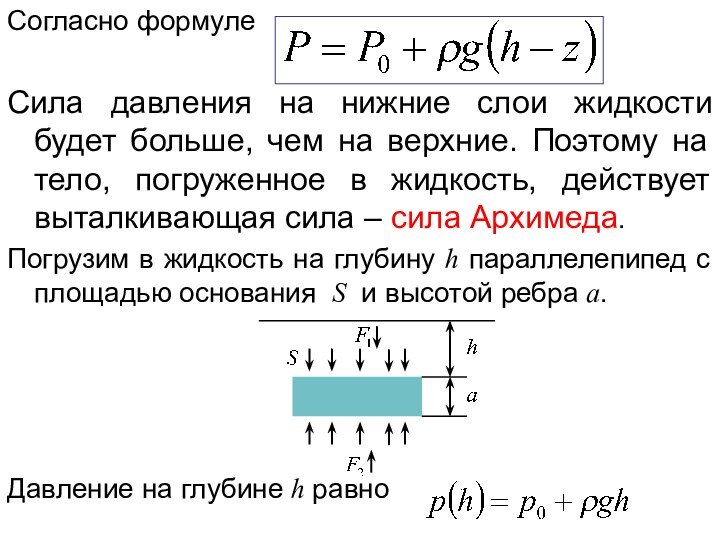
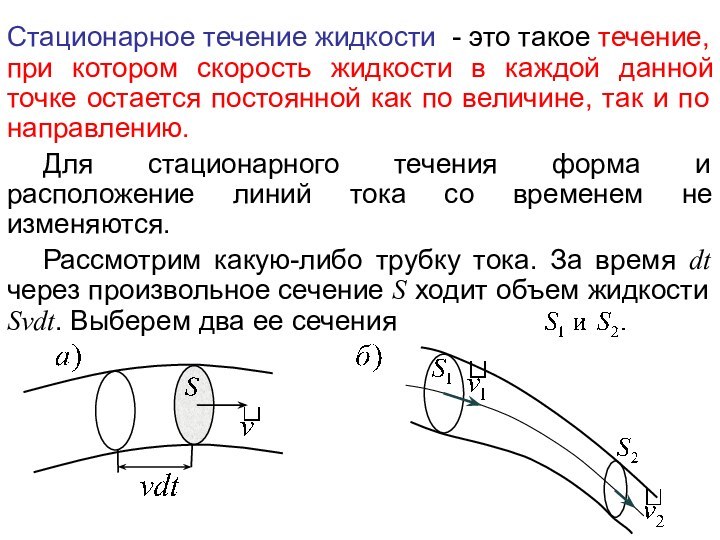
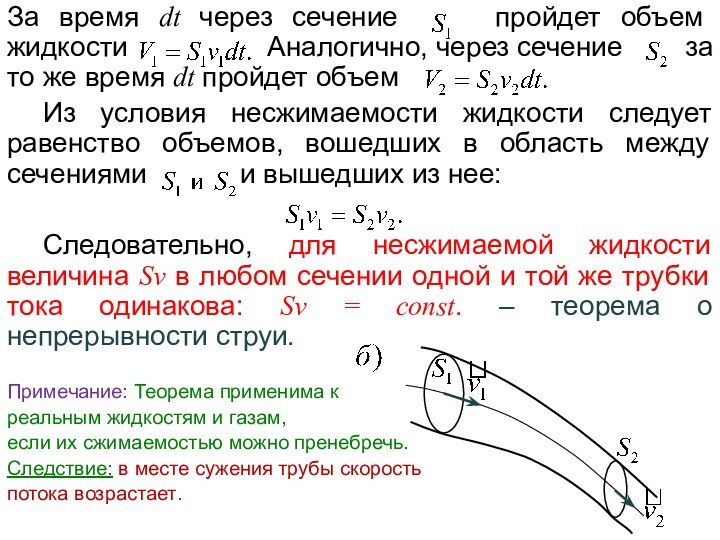
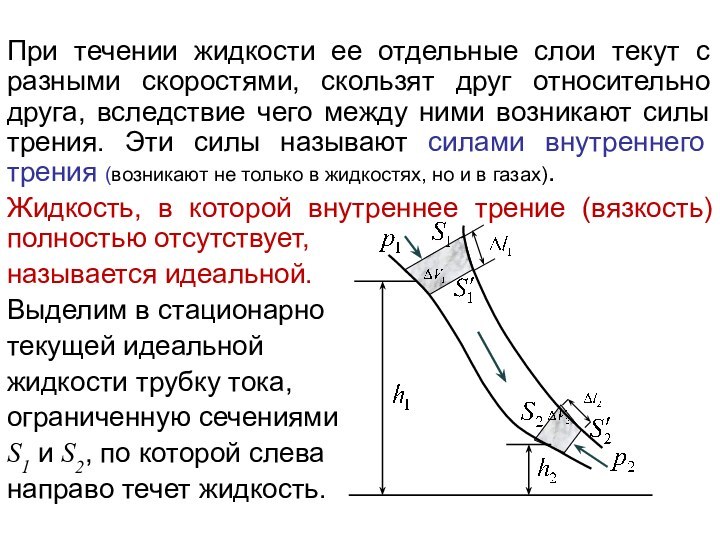
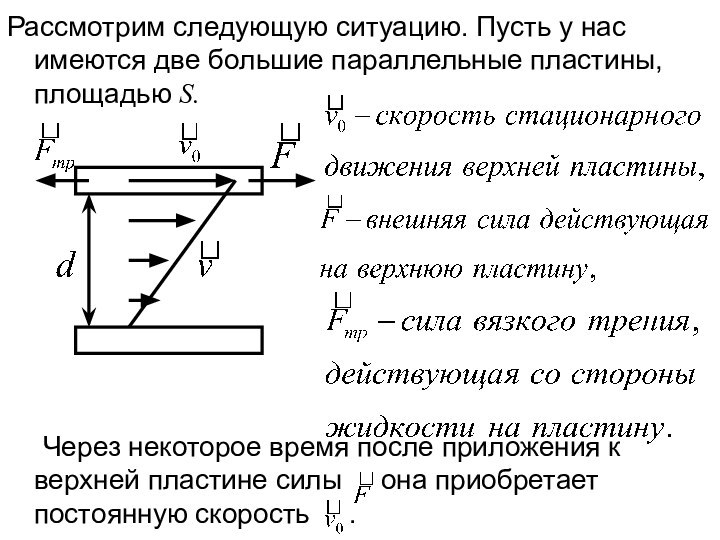
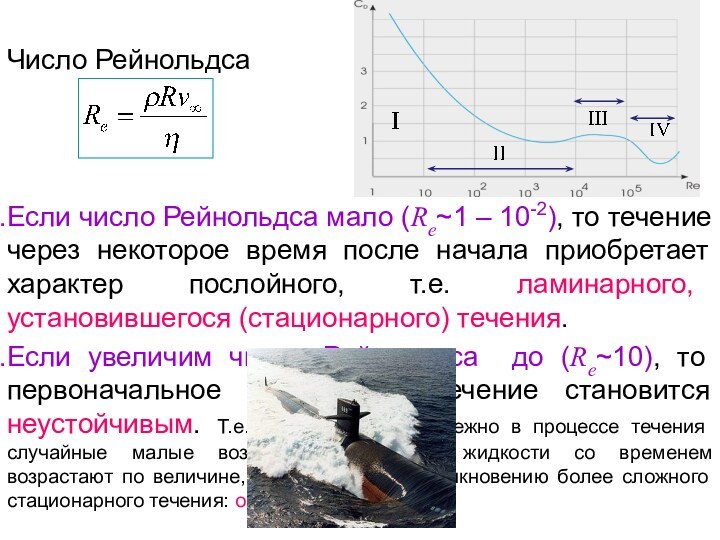
обладает свойством восстанавливать свои размеры и форму после того,

как деформирующие его силы прекращают свое воздействие.
Рассматриваем не сам процесс деформирования, а конечный результат, после установления равновесия в деформируемом теле.
Рассмотрим некоторое тело, деформированное внешними силами. Внешние силы вызывают смещения частиц тела по сравнению с исходным состоянием. В результате в теле возникают внутренние силы, т.е. тело переходит в напряженное состояние.

Слайд 4

Выделим бесконечно малый объем вещества в виде куба.

Обозначим

Выделим бесконечно малый объем вещества в виде куба. Обозначим dS – площадь

dS – площадь боковых граней куба.
В равновесии силы, действующие

на каждую грань:
Должны быть равны по величине и противоположны по направлению;
Полный момент всех сил, действующих на куб, равен нулю.

Слайд 5

Эти величины называются механическими напряжениями.
Из второго условия равновесия

Эти величины называются механическими напряжениями.Из второго условия равновесия суммарный момент, например,

суммарный момент, например, сил dF1y и dF2x равен нулю,

если dF1y = dF2x , т.е.

Слайд 6 Компоненты

Компоненты - нормальные напряжения, в зависимости от

- нормальные напряжения, в зависимости от знака

характеризуют растягивающие (сжимающие) усилия.
Напряжения - касательные (сдвиговые) напряжения, действуют в плоскости соответствующих граней.
При внешнем воздействии в общем случае тело изменяет свои размеры и форму, т.е. испытывает деформацию. При всем разнообразии деформаций оказывается возможным любую из них свести к двум.
Элементарными деформациями являются растяжение (сжатие) и сдвиг.

Слайд 7 Деформация растяжения (сжатия) –
характеризуют величиной относительного удлинения.
Если

Деформация растяжения (сжатия) – характеризуют величиной относительного удлинения.Если выделенный в теле

выделенный в теле объем до действия сил имел длину

l в некотором направлении, а после приложения сил, эта длина изменилась на Δ l, то относительное удлинение будет

При растяжении ε >0, при сжатии ε <0.
Как правило ε <<1 !!!

Слайд 8 Деформация сдвига
характеризуется величиной относительного сдвига

Закон Гука
Относительное растяжение

Деформация сдвига характеризуется величиной относительного сдвигаЗакон ГукаОтносительное растяжение (сжатие) ε пропорционально

(сжатие) ε пропорционально растягивающему (сжимающему) напряжению σ.

Е – модуль

Юнга – напряжение, создающее относительное удлинение тела, равное единице.

Слайд 9 Растяжение, например, стержня, сопровождается его поперечным сжатием.
-

Растяжение, например, стержня, сопровождается его поперечным сжатием. - относительное сжатие. Относительное сжатие

относительное сжатие.

Относительное сжатие связано с относительным растяжением:

-

коэффициент Пуассона.
«-» – отражает тот факт, что продольная и поперечная деформации при одноосном растяжении (сжатии) всегда имеют противоположные знаки.

Слайд 10 Зависимость напряжения от относительного
удлинения при растяжении образца

Предел упругости
Пластическая деформация
Деформационное упрочнение
Предел прочности
Текучее состояние

Слайд 11 2. Общие свойства жидкостей и газов

Слайд 12 Агрегатное состояния вещества
Твердое
Жидкое
Газообразное
Зависит от соотношения между

Агрегатное состояния веществаТвердое Жидкое ГазообразноеЗависит от соотношения между потенциальной энергией взаимодействия

потенциальной энергией взаимодействия атомов Wвз, составляющих тело, и их

средней кинетической энергией Wср.кин.
Wвз >> Wср.кин, твердое состояние.
Wвз ~ Wср.кин, жидкое состояние.
Wвз << Wср.кин, газообразное состояние.

Слайд 13 Способы кинематического описания жидкостей
Способ Лагранжа. Выбирается совокупность «жидких»

Способы кинематического описания жидкостейСпособ Лагранжа. Выбирается совокупность «жидких» частиц, движение жидкости

частиц, движение жидкости описывается как движение таких частиц. Вводится

понятие скорости и ускорения частиц (трудно учесть изменение формы «жидкой» частицы при движении).
Способ Эйлера. Задается векторное поле скоростей движения жидкости, т.е. фиксируем, как ведет себя скорость течения жидкости в точках ее объема с течением времени. Следим за кинематическими характеристиками жидкости в фиксированных точках пространства, не интересуясь тем, какие именно «жидкие» частицы проходят эти точки. Для наглядного представления вводят линии тока.

Слайд 14 Линия тока – линия, в каждой точке которой

вектор скорости направлен по касательной.

Густота , с

которой проведены линии тока, пропорциональна величине скорости течения.
Часть объема жидкости, ограниченная
линиями тока, называется трубкой тока.
Жидкость, находящаяся внутри трубки тока, не может покинуть ее пределы, т.к. по определению линий тока вектор скорости течения направлен по касательной к поверхности трубки тока.

Слайд 15 3. Поток вектора скорости; уравнение непрерывности

Слайд 16 Рассмотрим в поле вектора малый плоский элемент поверхности

Рассмотрим в поле вектора малый плоский элемент поверхности с площадью dS.

с площадью dS.
Введем единичный вектор положительной нормали

.
Образуем вектор площади элемента .
Потоком вектора через
поверхность бесконечно малой
площади называется величина:

объем dV, который успевает наполнять за 1 с поток жидкости, пронизывающий площадку dS

Слайд 17 Если поверхность имеет конечные размеры S

разбить на плоские малые элементы

поток вектора через

всю поверхность.
Здесь и далее считается, что нормаль к каждому из элементов поверхности dS направлена из объема наружу (внешняя нормаль).

если

исток

сток

если

Слайд 18 Рассмотрим в поле вектора малый

объем ΔV, окруженный замкнутой поверхностью ΔS. Тогда

будет характеризовать общую

интенсивность источников и стоков, находящихся в объеме ΔV.

характеризует удельную
интенсивность источников (стоков).

Это локальная удельная характеристика интенсивности источников жидкости в точке А поля .

Слайд 19

Если div(v) = 0, в т.

А нет источников (стоков).
Если div(v) > 0, т. А

является источником.
Если div(v) < 0, т. А является стоком.
Чем больше div(v) > 0, тем выше интенсивность источника.

Это локальная удельная характеристика интенсивности источников жидкости в точке А поля .

Слайд 20 Уравнение непрерывности
Выберем в жидкости объем V, ограничим замкнутой

Уравнение непрерывностиВыберем в жидкости объем V, ограничим замкнутой поверхностью S. Поток

поверхностью S. Поток массы через S:

Масса жидкости, заключенной внутри

S, равна

В отсутствие источников (стоков) жидкости внутри объема масса жидкости, которая вытекает из него, должна быть равна изменению массы объема V в единицу времени, т.е. .

Слайд 21

Уравнение непрерывности жидкости в интегральной форме.
Если течение стационарно,

Уравнение непрерывности жидкости в интегральной форме.Если течение стационарно, т.е. величины, характеризующие

т.е. величины, характеризующие течение жидкости, не зависят явно от

времени, то
Смысл: в стационарном потоке
сколько жидкости входит в данный объем, столько и выходит из него.

Слайд 22 4. Циркуляция векторного поля. Ротор вектора. Уравнения движения

и равновесия жидкости.

Слайд 23 Пусть в поле скоростей v (x, y, z)

Пусть в поле скоростей v (x, y, z) задана некоторая кривая

задана некоторая кривая L. Разобьем
эту кривую на малые

векторные
элементы dl, направление
которых совпадает с
направлением обхода L.
циркуляция вектора скорости
вдоль кривой L (характеризует завихренность поля вектора в области расположения L).

Слайд 24 Это локальная характеристика завихренности потока жидкости в окрестности

точки А.

Слайд 25 В жидкости отсутствует понятие сдвига. В жидкости могут

В жидкости отсутствует понятие сдвига. В жидкости могут быть только напряжения

быть только напряжения всестороннего сжатия, причем

где Р – давление

– сила, действующая на некоторую площадку, помещенную в жидкость перпендикулярно силе и отнесенной к единице площади:

Слайд 26 Выберем в жидкости бесконечно малый объем
dx, dy, dz

– длины ребер.

P(x, y, z, t) – давление жидкости вблизи левой боковой грани, перпендикулярной оси y,
P(x, y +dy, z, t) – давление жидкости вблизи правой боковой грани.
Проекция на ось y силы давления жидкости:

Слайд 27 Воспользуемся определением частной производной , т е. проекция

Воспользуемся определением частной производной , т е. проекция силы давления, отнесенная

силы давления, отнесенная к единице объема:

Аналогично:

Сила давления, действующая

на элемент жидкости.
Учтем, что жидкость может находиться в гравитационном поле, потенциал которого ϕ, тогда - сила, действующая со стороны этого поля на единицу массы.
-сила, отнесенная к единице объема.

Слайд 28 Идеальная жидкость – жидкость, вязкостью которой можно пренебречь.
Запишем

второй закон Ньютона

Уравнение движения идеальной жидкости в гравитационном поле
В равновесии справедлив закон Паскаля: давление, оказываемое на жидкость, передается ею по всем направлениям одинаковым образом.

Слайд 29 Частный случай: несжимаемая жидкость.
Жидкость находится в однородном поле

Частный случай: несжимаемая жидкость.Жидкость находится в однородном поле тяготения.Выберем положительное направление

тяготения.
Выберем положительное направление оси z вертикально верх. Тогда потенциал

будет

где g – ускорение свободного падения. Подставим в уравнение равновесия:

линейное увеличение гидростатического давления с увеличением глубины

Слайд 30 Одно из проявлений закона Паскаля можно наблюдать в

Одно из проявлений закона Паскаля можно наблюдать в гидравлическом прессе: два

гидравлическом прессе: два сообщающихся сосуда заполнены жидкостью и закрыты

поршнями различной площади. По закону Паскаля, давления под поршнями одинаковы:

Таким образом, сила давления второго поршня больше силы давления первого во столько раз, во сколько площадь больше первого.
Гидравлический пресс – простой механизм, позволяющий развить колоссальные силы, используемые для прессования различных изделий из металлов и пластмасс.
Обозначим - ходы поршней.

Слайд 31 Вследствие несжимаемости объемы жидкости, перешедшего из одного цилиндра

Вследствие несжимаемости объемы жидкости, перешедшего из одного цилиндра в другой, одинаковы: Работы,

в другой, одинаковы:
Работы, совершаемые силами за один ход

Их отношение

Как

и следовало ожидать,
пресс дает выигрыш в силе, но не в совершаемой работе.

Слайд 32 Согласно формуле

Сила давления на нижние слои жидкости будет

Согласно формулеСила давления на нижние слои жидкости будет больше, чем на

больше, чем на верхние. Поэтому на тело, погруженное в

жидкость, действует выталкивающая сила – сила Архимеда.
Погрузим в жидкость на глубину h параллелепипед с площадью основания S и высотой ребра a.

Давление на глубине h равно

Слайд 33 Поэтому на верхнее основание действует сила

На глубине h

Поэтому на верхнее основание действует силаНа глубине h + a давление

+ a давление равно

Поэтому на нижнее основание действует сила

Равнодействующая

этих двух сил направлена вверх и равна по величине

Здесь - объем погруженной части тела,
- масса жидкости (газа) того же объема.
Закон Архимеда: на тело погруженное в жидкость (газ), действует выталкивающая сила, равна весу вытесненной телом жидкости (газа).

Слайд 34 6. Стационарное движение идеальной жидкости. Уравнение Бернулли

Слайд 35 Стационарное течение жидкости - это такое течение, при

Стационарное течение жидкости - это такое течение, при котором скорость жидкости

котором скорость жидкости в каждой данной точке остается постоянной

как по величине, так и по направлению.
Для стационарного течения форма и расположение линий тока со временем не изменяются.
Рассмотрим какую-либо трубку тока. За время dt через произвольное сечение S ходит объем жидкости Svdt. Выберем два ее сечения

Слайд 36 За время dt через сечение пройдет

объем жидкости

Аналогично, через сечение за то же время dt пройдет объем
Из условия несжимаемости жидкости следует равенство объемов, вошедших в область между сечениями и вышедших из нее:

Следовательно, для несжимаемой жидкости величина Sv в любом сечении одной и той же трубки тока одинакова: Sv = const. – теорема о непрерывности струи.

Примечание: Теорема применима к
реальным жидкостям и газам,
если их сжимаемостью можно пренебречь.
Следствие: в месте сужения трубы скорость
потока возрастает.

Слайд 37
При течении жидкости ее отдельные слои текут с

При течении жидкости ее отдельные слои текут с разными скоростями, скользят

разными скоростями, скользят друг относительно друга, вследствие чего между

ними возникают силы трения. Эти силы называют силами внутреннего трения (возникают не только в жидкостях, но и в газах).
Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует,
называется идеальной.
Выделим в стационарно
текущей идеальной
жидкости трубку тока,
ограниченную сечениями
S1 и S2, по которой слева
направо течет жидкость.

Слайд 38
За время Δt объем жидкости переместится вдоль трубки

За время Δt объем жидкости переместится вдоль трубки тока. В силу

тока. В силу непрерывности струи заштрихованные объемы будут иметь

одинаковую величину:
Энергия каждой частицы жидкости
Полная энергия потока, протекающего за Δt через сечение S1

Аналогично для S2

Слайд 39 Изменение полной механической энергии

Силы давления на боковую поверхность

Изменение полной механической энергииСилы давления на боковую поверхность трубки тока перпендикулярны

трубки тока перпендикулярны в каждой точке к направлению перемещения

частиц, поэтому работу не совершают. Отлична от нуля только работа сил, приложенных к сечениям S1 и S2.

Слайд 40 Сечения S1 и S2 были взяты произвольно. Поэтому

Сечения S1 и S2 были взяты произвольно. Поэтому в стационарно текущей

в стационарно текущей идеальной жидкости в любом сечении трубки

выполняется условие:

Уравнение Бернулли: в установившемся движении идеальной жидкости полное давление, слагающееся из динамического, гидростатического и статического, одинаково для всех поперечных сечений трубки тока.

Слайд 41 7. Движение тел в среде с сопротивлением. Стационарное

течение вязкой жидкости

Слайд 42 Рассмотрим следующую ситуацию. Пусть у нас имеются две

Рассмотрим следующую ситуацию. Пусть у нас имеются две большие параллельные пластины,

большие параллельные пластины, площадью S.

Через некоторое время после приложения

к верхней пластине силы она приобретает постоянную скорость .

Слайд 43 Слои жидкости также станут двигаться, причем величина скорости

Слои жидкости также станут двигаться, причем величина скорости этих слоев будет

этих слоев будет линейно возрастать от 0 до ∞

с увеличением расстояния от нижней пластины.
Выводы:
1. Вязкая жидкость «прилипает» к поверхности твердого тела. Скорость жидкости на поверхности тела и скорость тела движущегося в жидкости одинаковы (условие «прилипания»).
2. Так как скорость постоянна, то со стороны жидкости на верхнюю пластину действует сила, которая компенсирует внешнюю силу . Это и есть сила вязкого трения . Она действует не только на твердые тела в жидкости, но и между элементами самой жидкости.

Слайд 44 Для величины силы вязкого трения в условиях рассматриваемого

Для величины силы вязкого трения в условиях рассматриваемого опыта справедливо равенствоФормула

опыта справедливо равенство

Формула Ньютона

- коэффициент вязкости –

динамическая вязкость

Уравнение движения вязкой жидкости – уравнение Навье-Стокса
Применяется для описания движения реальных жидкостей и газов

Слайд 45

Вихревая дорожка при обтекании цилиндра

Слайд 46
Число Рейнольдса

Если число Рейнольдса мало (Re~1 – 10-2),

Число РейнольдсаЕсли число Рейнольдса мало (Re~1 – 10-2), то течение через

то течение через некоторое время после начала приобретает характер

послойного, т.е. ламинарного, установившегося (стационарного) течения.
Если увеличим число Рейнольдса до (Re~10), то первоначальное ламинарное течение становится неустойчивым. Т.е. возникающие неизбежно в процессе течения случайные малые возмущения скорости жидкости со временем возрастают по величине, что приводит к возникновению более сложного стационарного течения: образуются два вихря.

Слайд 47

Слайд 48 3. Если увеличить число Рейнольдса до (Re~102), то

3. Если увеличить число Рейнольдса до (Re~102), то характер течения снова

характер течения снова меняется за счет нового типа неустойчивости:

возникает нестационарное обтекание, при котором вихри отрываются и уносятся по течению.
4. Если увеличить число Рейнольдса до (Re~104-105), течение становится полностью неупорядоченным, хаотическим. Такое течение называет турбулентным.

Слайд 49

Ламинарное (на переднем плане) и турбулентное течение вокруг

субмарины «Лос-Анджелес»

Слайд 50

- Предыдущая К.И.Чуковский. Сказки

Следующая - Ученическое самоуправление

Физика пәнінен презентация Лоренц күші (10 сынып) 242

Атмосфера и атмосферное давление 144

Ученический проект по теме: Конденсаторы и электроемкость. 10 класс 163

Презентация по физике на тему Исследование морских глубин (7 класс) 503

Химия питания 155

Физика твёрдого тела 138

Исследование жизни 131

Магнитное поле земли и его влияние на живые организмы 171

Геотермальная энергия 145

Альберт Эйнштейн 121

Законы Кеплера (11 клас) 141

Презентация по физике 7 класс Расчёт пути и времени движения 157

Электрическое напряжение. Вольтметр 138

Презентация по физике на тему: Газовые законы.Изопроцессы 194

Методика запоминания некоторых формул на уроках физики 195

Физика электромагнитная индукция 137

Теорема Гаусса (закон Гаусса) 139

Энергопотребление и энергосбережение в быту. 129

Измерение физических величин 159

Теория электролитической диссоциации 142

Механические явления в природе 151

Презентация по физике. 7 класс. Атмосферное давление 133

Презентация к уроку Простые механизмы 136

Излучающие и приёмные элементы. (Тема 2.2) 113