Слайд 3
Цель исследования – выяснить причины возникновения
зрительных иллюзий
с точки зрения геометрии; показать значимость
математических законов
для
искусства, живописи.
Гипотеза – зрительные иллюзии можно обосновать с
помощью геометрических законов,
а «волшебство» зрительных иллюзий обосновать
математически.
Задачи работы:
изучить теоретический материал по данному вопросу;
выяснить, что такое зрительно-геометрические иллюзии;
рассмотреть примеры геометрических иллюзий;
показать область применения математических иллюзий
в работе художника, объяснить и доказать их с точки
зрения геометрии;
создать коллекцию иллюзий.
Слайд 4
Иллю́зия (лат. illusio — заблуждение, обман) — искажённое восприятие реально существующего объекта или явления, допускающее неоднозначную интерпретацию
Зрительная иллюзия –
ошибка в зрительном восприятии; искажение пространственных соотношений признаков воспринимаемых
объектов.
Слайд 5
Самые известные зрительные иллюзии
и обман зрения на
сегодняшний день
представлены:
Иллюзиями восприятия цвета,
Контрастными иллюзиями,
Искривляющими иллюзиями,
Контурными
иллюзиями,
Иллюзиями восприятия глубины,
Иллюзиями восприятия размера,
Иллюзиями-перевёртышами,
Стерео-иллюзиями,
Движущимися иллюзиями.
Слайд 6
Иллюзия восприятия цвета
«иллюзия тени Адельсона»
В
каждом прямоугольнике правая часть
(в треугольнике) кажется темнее, чем
левая,
хотя на самом деле, яркость одинаковая.
Слайд 7
Иллюзия восприятия глубины
Решетка Геринга (иллюзия мерцающей решетки)
Слайд 8
Иллюзии-перевёртыши
Что вы видите: огромную ворону с
добычей
или
рыбака в лодке, рыбу и остров с деревьями?
Слайд 9
Оптико-геометрические иллюзии.
1. Иллюзия Мюллера-Лайера
Несмотря на то, что горизонтальные
отрезки равной длины, в зависимости от «оперения» их длина
представляется разной. Нижняя часть рисунка показывает, что отрезки на самом деле одинаковые.
Слайд 10
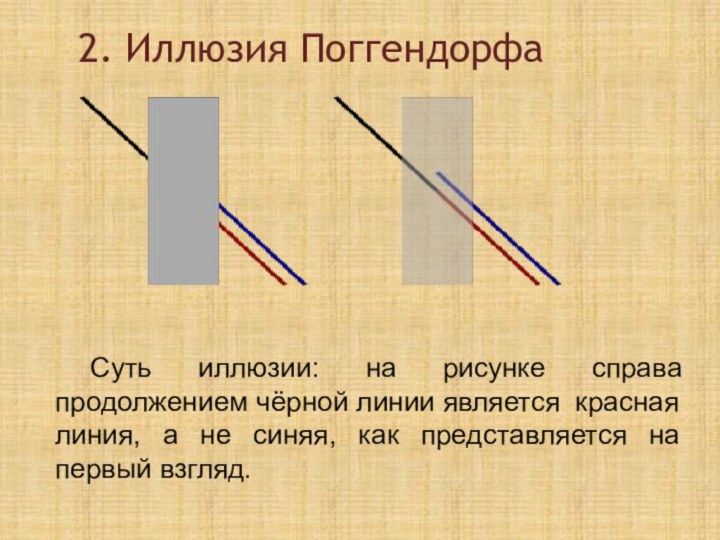
2. Иллюзия Поггендорфа
Суть иллюзии: на рисунке справа продолжением
чёрной линии является красная линия, а не синяя, как
представляется на первый взгляд.
Слайд 12
4. Иллюзия параллелограмов
(Параллелограмм Зендера)
Поразительную иллюзию создают углы
– тупой
и острый; диагонали АВ и ВС двух
параллелограмов равны, хотя диагональ ВС
кажется гораздо короче.
Слайд 13
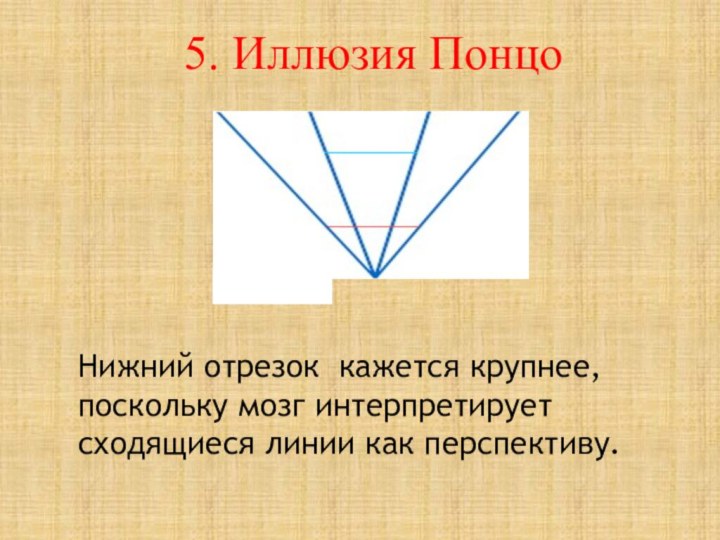
5. Иллюзия Понцо
Нижний отрезок кажется крупнее, поскольку мозг
интерпретирует сходящиеся линии как перспективу.
Слайд 14
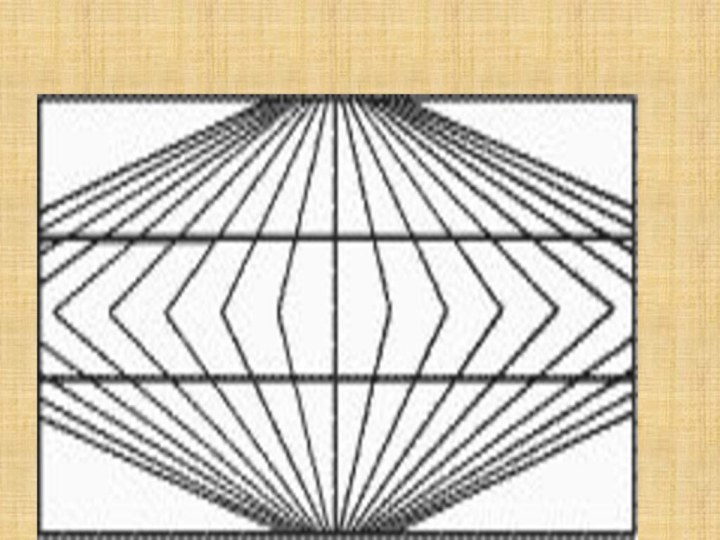
6. Иллюзия Перельмана
Несмотря на то, что каждая линия
кажется здесь не
параллельной, оказалось, что параллельность для них
выполняется.
Слайд 15
Применение математических иллюзий в живописи
Голландский художник Мориц Корнилис
Эшер написал:
«В математических работах регулярное разбиение плоскости
рассматривается теоретически...
Значит ли это, что данный вопрос является
сугубо математическим?
Математики открыли дверь ведущую в другой мир,
но сами войти в этот
мир не решились. Их больше интересует путь, на котором
стоит дверь, чем сад, лежащий за ней.»
Слайд 17
Форма пространства
Литография «Три
пересекающиеся плоскости»
Работа «Змеи»
Слайд 19
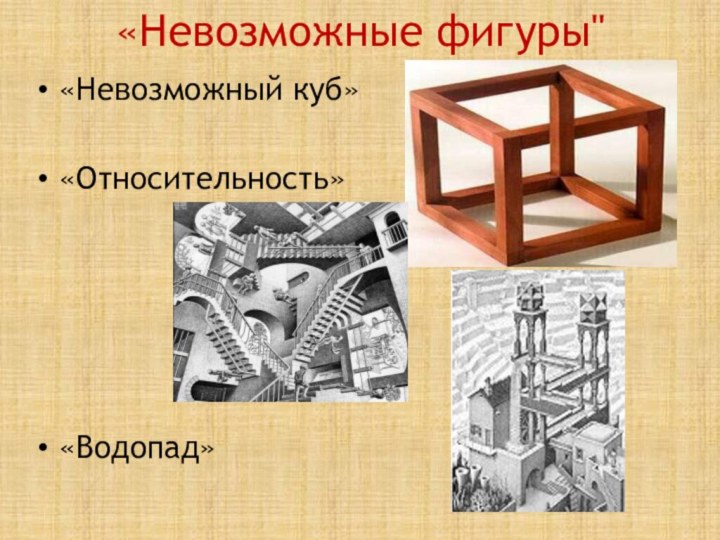
«Невозможные фигуры"
«Невозможный куб»
«Относительность»
«Водопад»
Слайд 20
Выводы:
Математические иллюзии показывают, что не всегда можно верить
тому, что видишь;
Мы часто полагаем, что реально только то,
что у нас перед глазами.
Математические иллюзии отражают наличие неочевидного в жизни
Игры с математическими иллюзиями помогают изменять сознание –
мы хитростью заманиваем мозг на новые уровни восприятия, мы
начинаем видеть то, чего нет.
Восприятие размера иллюзии часто приводят к совершенно
неверным количественным оценкам реальных размеров и
величин.
Оказывается, что можно ошибиться на 25 % и больше, если
глазомерные оценки не проверить линейкой.
Математические иллюзии – оригинальный и необычный способ
создания достояний живописи.
Слайд 21
Попробуем изобразить иллюзию самостоятельно, в виде абстрактного рисунка.
Слайд 22
Результаты анкетирования:
Иллюзия Мюллера-Лайера
Равны ли отрезки?
Слайд 23
Иллюзия Поггендорфа
Какая линия является продолжением
черной?
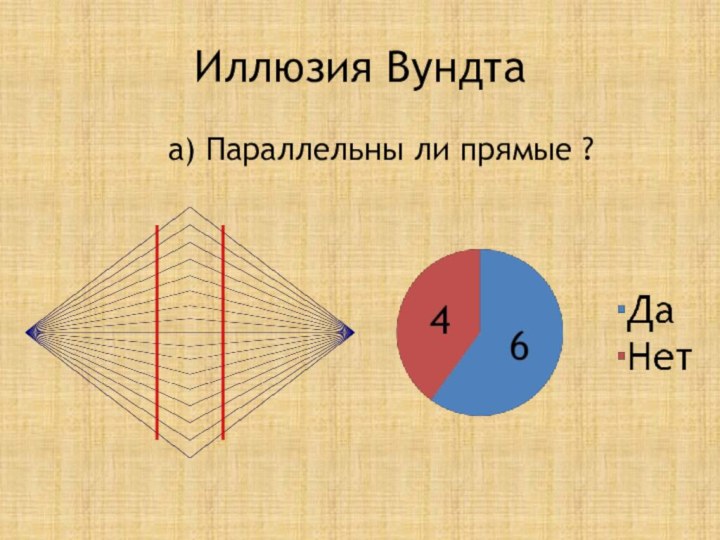
а) Параллельны ли прямые ?
Слайд 25
Иллюзия Вундта
б) Равны
ли отрезки?
Слайд 26
Иллюзия параллелограммов (параллелограмм Зендера)
Равны ли диагонали АВ
и ВС?