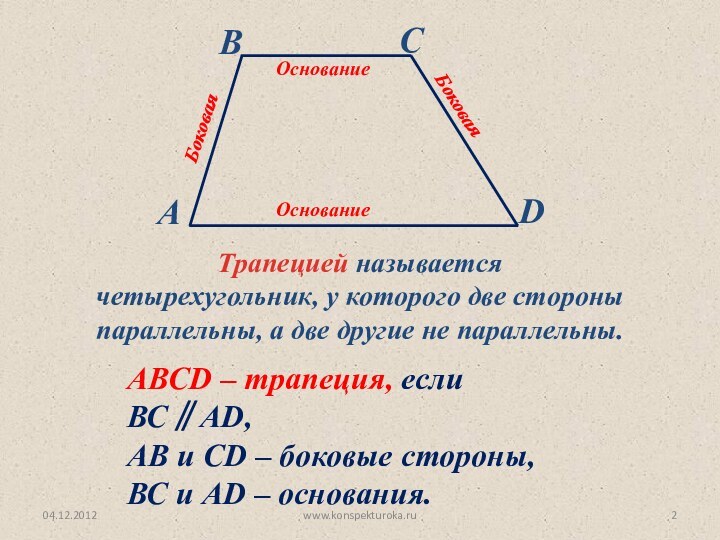
а две другие не параллельны.
АВСD – трапеция, если ВС∥AD,
АВ и СD – боковые стороны,
ВС и AD – основания.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

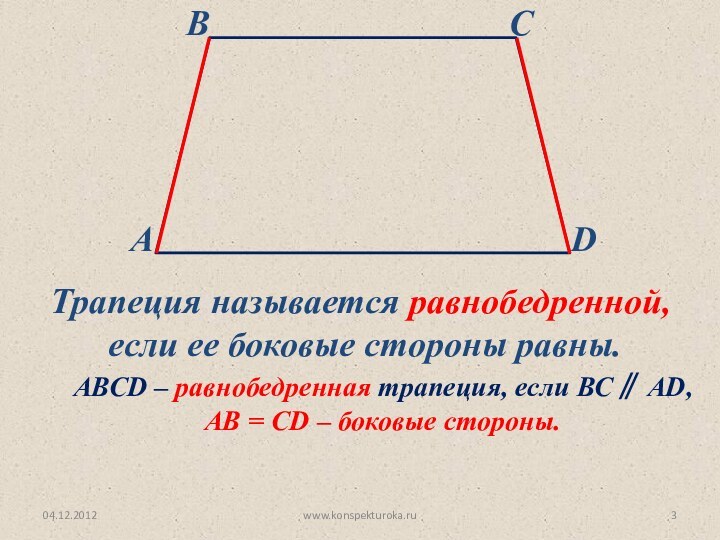
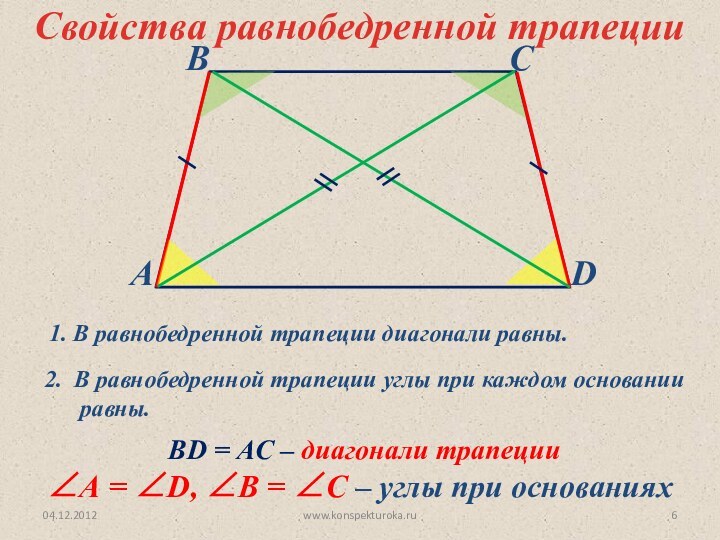

1. В равнобедренной трапеции диагонали равны.
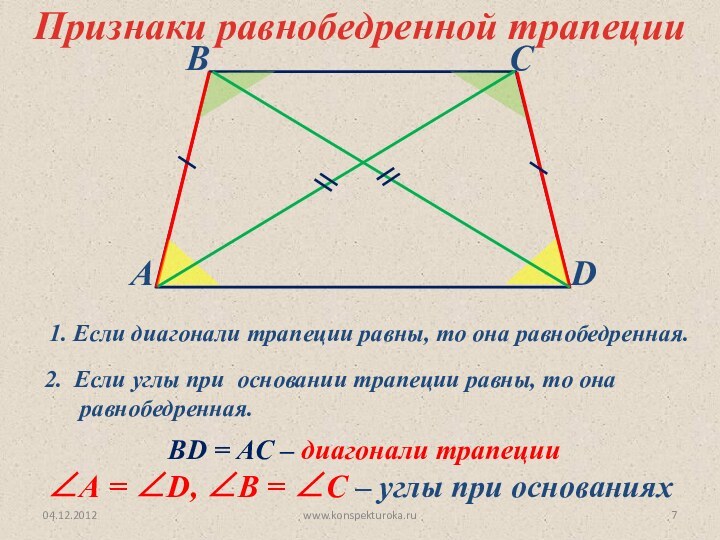
1. Если диагонали трапеции равны, то она равнобедренная.
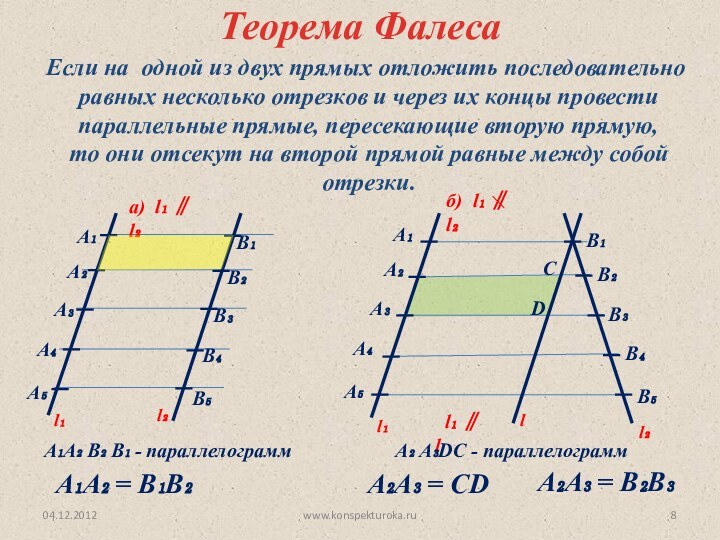
а) l₁ ∥ l₂
б) l₁ ∥ l₂
А₁А₂ = В₁В₂
l₁
l₁
l₂
l₂
А₁А₂ В₂ В₁ - параллелограмм
l₁ ∥ l
А₂ А₃DC - параллелограмм
А₂A₃ = CD
А₂A₃ = В₂B₃
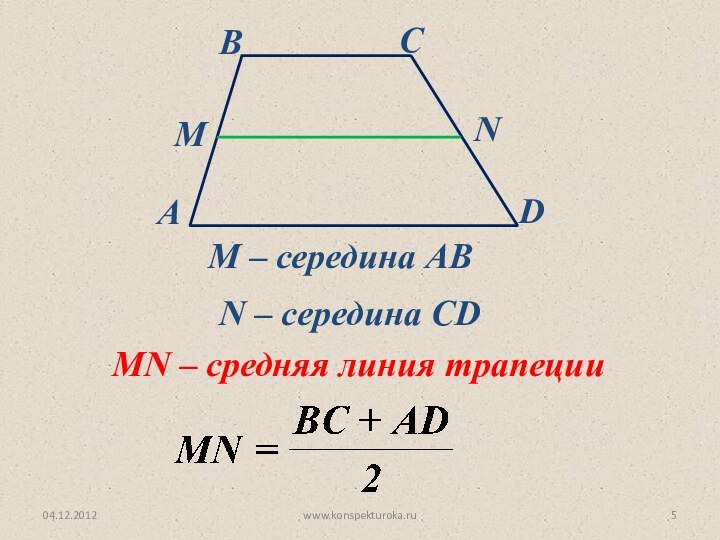
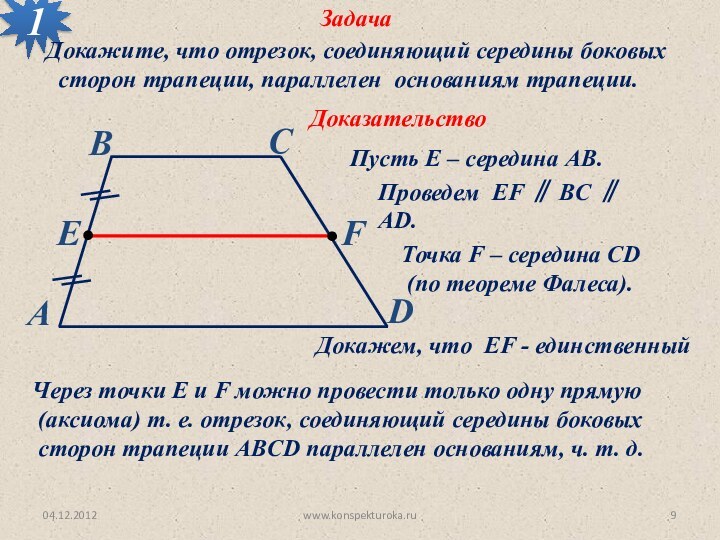
Точка F – середина CD
(по теореме Фалеса).
Докажем, что ЕF - единственный
Через точки Е и F можно провести только одну прямую
(аксиома) т. е. отрезок, соединяющий середины боковых
сторон трапеции ABCD параллелен основаниям, ч. т. д.
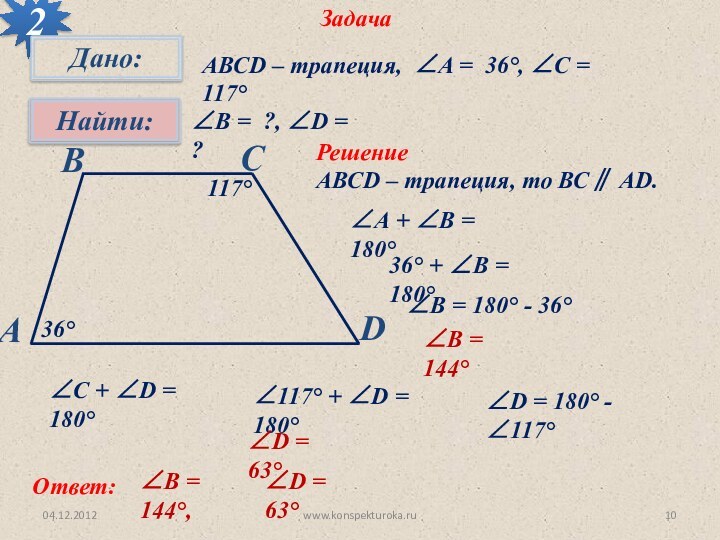
∠А + ∠В = 180°
36° + ∠В = 180°
∠В = 180° - 36°
∠В = 144°
∠С + ∠D = 180°
∠117° + ∠D = 180°
∠D = 180° - ∠117°
∠D = 63°
Ответ:
∠В = 144°,
∠D = 63°
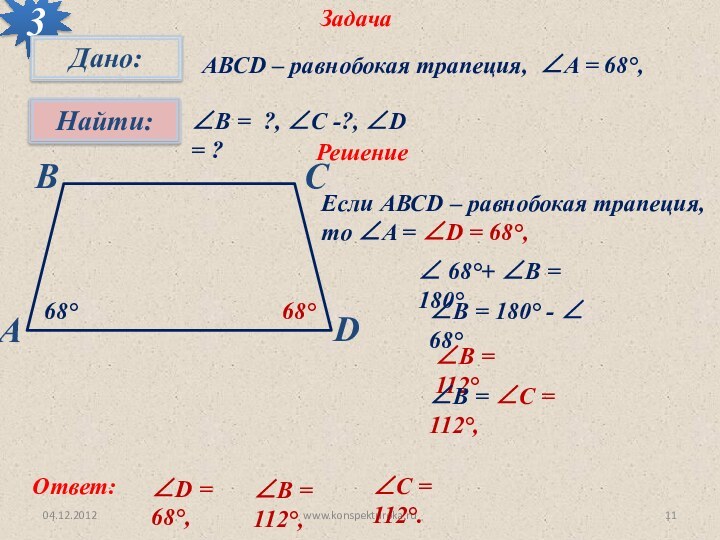
68°
68°
∠ 68°+ ∠В = 180°
∠В = 180° - ∠ 68°
∠В = 112°
∠В = ∠С = 112°,
Ответ:
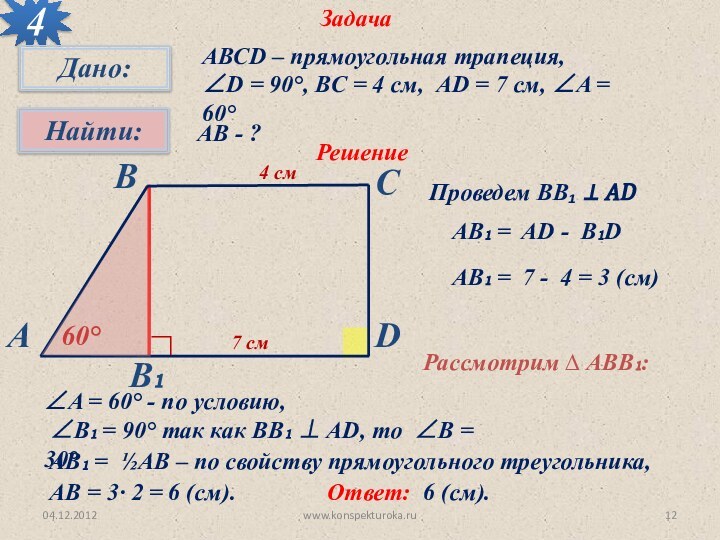
АВ - ?
Решение
Проведем ВВ₁ ⊥ AD
4 см
7 см
60°
AВ₁ = AD - B₁D
AВ₁ = 7 - 4 = 3 (см)
Рассмотрим ∆ АBВ₁:
∠A = 60° - по условию,
∠В₁ = 90° так как ВВ₁ ⊥ AD, то ∠В = 30°
AВ₁ = ½АВ – по свойству прямоугольного треугольника,
АВ = 3· 2 = 6 (см).
Ответ:
6 (см).