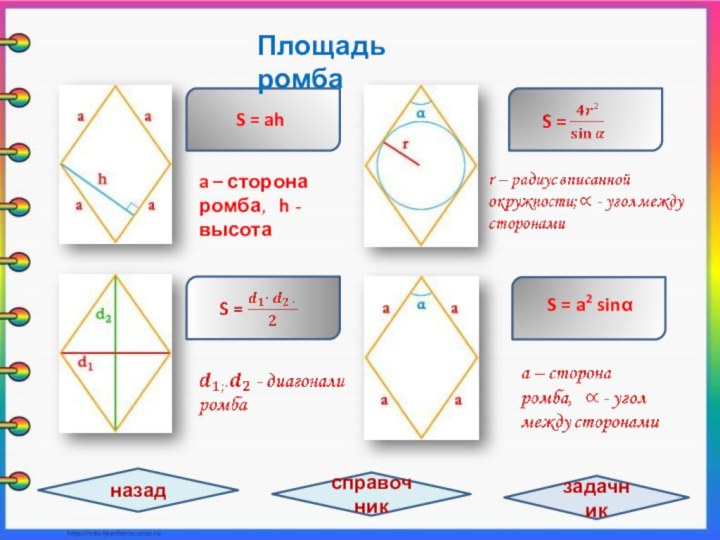
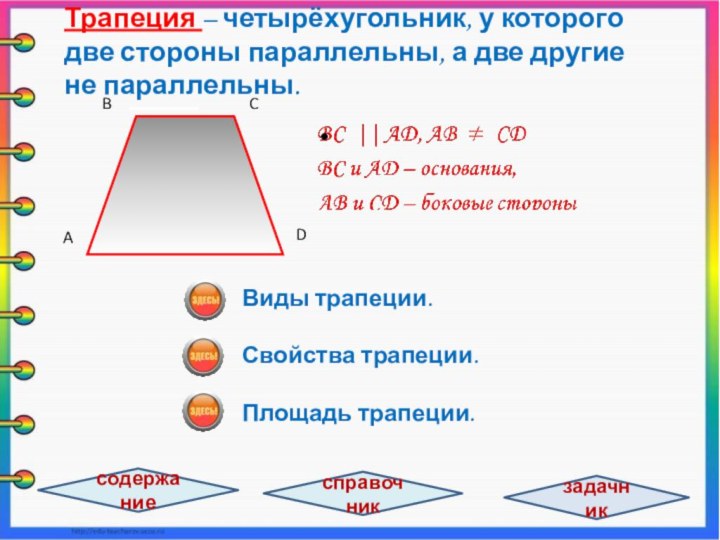
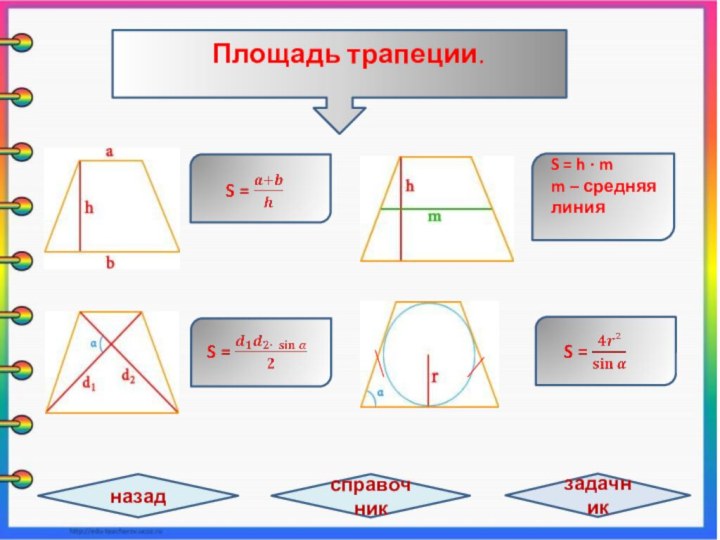
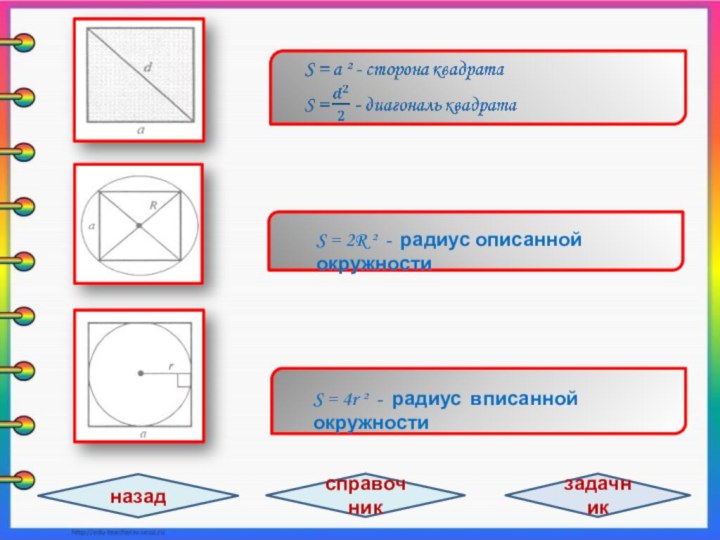
задачи не хватает знания какой-то одной-единственной формулы, которую хочется
быстрее найти и применить, но не всегда эта формула находится под рукой, поэтому в презентации собраны самые важные и нужные формулы по теме «Четырёхугольники», которые могут понадобятся при решении различных заданий., а так же при самоподготовке к ЕГЭ /11 класс/ и ОГЭ /9 класс/.Номинация: интерактивная презентация к урокам