- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора по геометрии
Содержание
- 2. Теорема Пифагора "Пифагоровы штаны Во все стороны равны" (Исторический экскурс)
- 4. Без преувеличения можно сказать, что это самая
- 5. Теорема Пифагора – одна из самых главных
- 6. В чем же причина такой популярности «пифагоровых
- 8. Пифагор – древнегреческийПифагор – древнегреческий ученый (VIVI
- 9. Так на юге Италии, которая была в
- 10. Достоверно известно, что Пифагор много
- 11. Именно Пифагору приписывают и доказательство знаменитой геометрической
- 13. Доказательство теоремы считалось в кругах учащихся средних
- 14. Теорему называли «мостом ослов», так как слабые
- 15. «В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 16. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 17. Итак, Если дан нам треугольник И притом с прямым
- 18. ЗадачаР е ш е н и е
- 19. ЗадачаР е ш е
- 20. ЗадачаР е ш е н и е
- 21. Не подлежит, однако, сомнению, что эту теорему
- 22. Это же самое проделывалось тысячи лет назад
- 24. К теореме Пифагора его ученики составляли
- 25. С глубокой древности математики находят все новые
- 26. В самом древнем индийском геометрическом сборнике «Сульвасутра»
- 27. Различные способы доказательства теоремы Доказательства, основанные на
- 28. В Древнем Вавилоне это свойство не только
- 29. Среди многочисленных доказательств теоремы Пифагора методом разложения
- 30. Большая часть доказательств теоремы Пифагора выполнена геометрическими
- 31. В трактате «Математика в девяти книгах», созданном
- 33. 125^2 = 117^2 + Х^2X^2 = 125^2
- 34. Часто математики записывали свои задачи в стихотворной
- 35. Старинные задачи:
- 36. Решение:3^2 + 4^2 = x^2X^2 = 25X
- 37. Еще одна задача древних индусов также предложенная в стихах:
- 38. Решение:(Х + ½)^2 – X^2 = 2^2X^2
- 39. Сейчас теорему Пифагора знают практически все, кто
- 40. Источники информации:www.1september.ru/ruhttp://root/И. Глейзер. История математики в школе.//images.yandex.ru/yandsearch?А.Д.Александров
- 41. Теорема.В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 42. Доказательство:Достроим данный треугольник до квадрата со стороной
- 43. Дано: ∆АВС – прямоугольный а = ВС
- 44. Скачать презентацию
- 45. Похожие презентации





























Слайд 4 Без преувеличения можно сказать, что это самая известная
теорема геометрии, ибо о ней знает подавляющее большинство населения
планеты, хотя доказать ее способна лишь очень незначительная его часть.Теорема Пифагора!
Слайд 5 Теорема Пифагора – одна из самых главных теорем
геометрии. Из нее или с ее помощью можно вывести
большинство теорем. Сама же теорема Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагу.
Слайд 6
В чем же причина такой популярности
«пифагоровых штанов»?
б) простота,
а) красота,
в) значимость.
Знатоки утверждают,
что причин здесь три:Слайд 8 Пифагор – древнегреческийПифагор – древнегреческий ученый (VIVI в.
до н.э.)
Знаменитый греческий философ и математик Пифагор
Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко недостоверны. С его именем связано много легенд.
Слайд 9
Так на юге Италии, которая была в то
время греческой колонией, возникла знаменитая «Пифагорейская школа», сыгравшая важную
роль в научной и политической жизни древней Греции.Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. Однако, в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.
Слайд 10 Достоверно известно, что Пифагор много путешествовал
по странам Востока, посещал Египет, Индию и Вавилон, изучал
древнюю культуру и достижения науки разных стран.Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии, куда принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя.
Слайд 11 Именно Пифагору приписывают и доказательство знаменитой геометрической теоремы.
На основе преданий, распространенных известными математиками (Прокл, Плутарх и
др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили тайной имя своего учителя, так что установить правду о Пифагоре невозможно.
Слайд 13
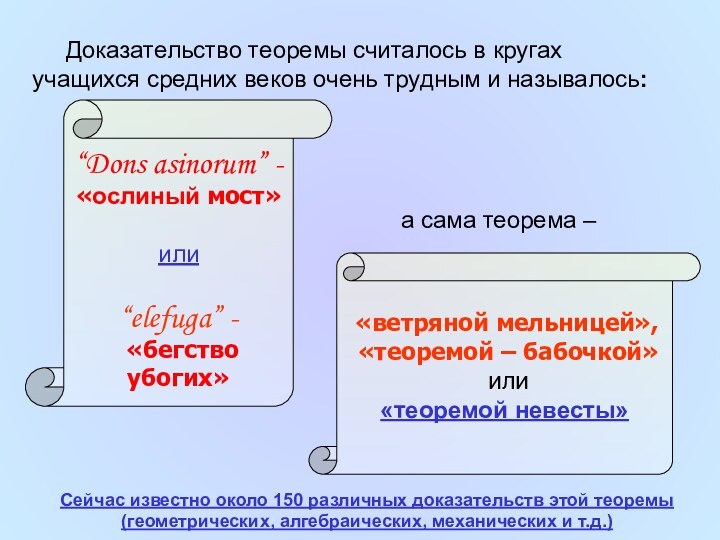
Доказательство теоремы считалось в кругах учащихся средних веков
очень трудным и называлось:
Сейчас известно около 150 различных
доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)
“Dons asinorum” -
«ослиный мост»
или
“elefuga” -
«бегство убогих»
«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
а сама теорема –
Слайд 14 Теорему называли «мостом ослов», так как слабые ученики,
заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами»,
были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
"Dons asinorum"
"elefuga"
Слайд 15
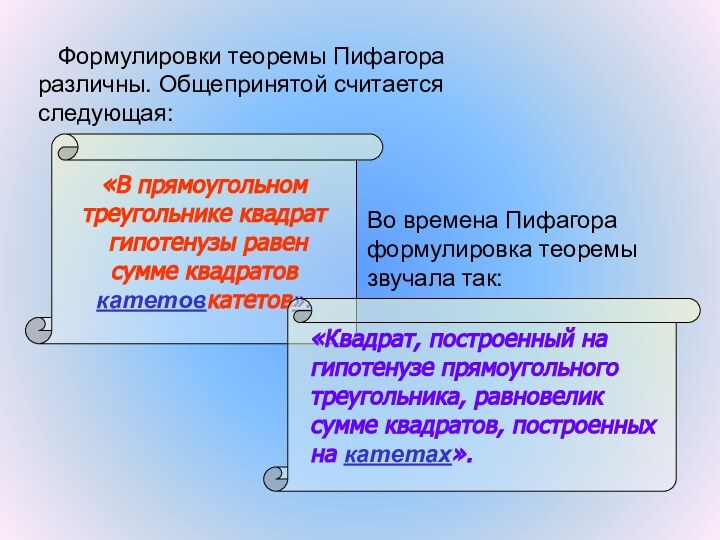
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Формулировки теоремы Пифагора различны. Общепринятой считается следующая:
Во
времена Пифагора формулировка теоремы звучала так:
Слайд 17
Итак,
Если дан нам треугольник
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней
находим – И таким простым путём
К результату мы придём.
Ч.т.д.
Теорема в стихах
Слайд 18
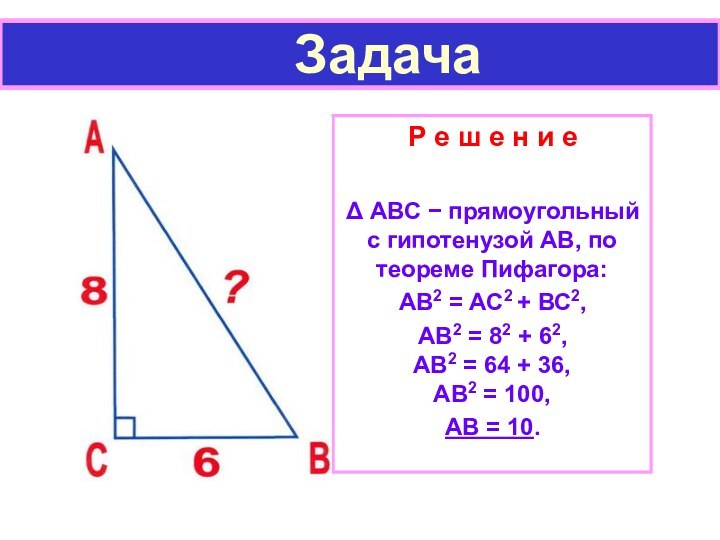
Задача
Р е ш е н и е
Δ АВС − прямоугольный с гипотенузой АВ, по теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
Слайд 19
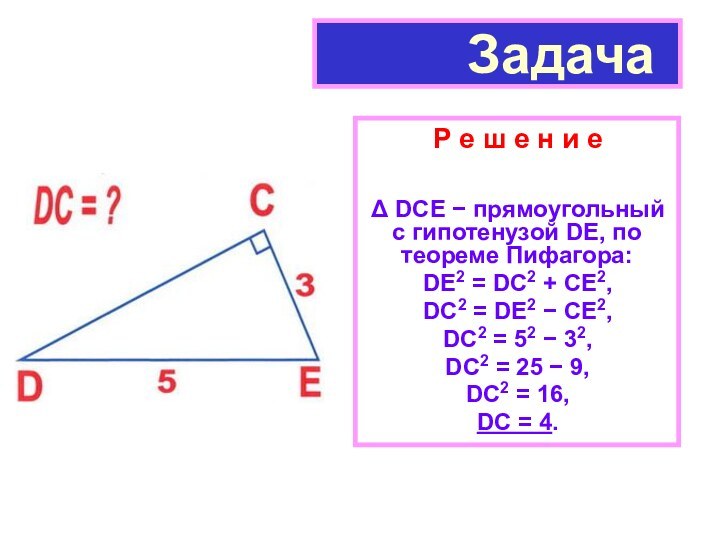
Задача
Р е ш е н
и е
Δ DCE − прямоугольный с гипотенузой DE, по
теореме Пифагора: DE2 = DС2 + CE2,
DC2 = DE2 − CE2,
DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
Слайд 20
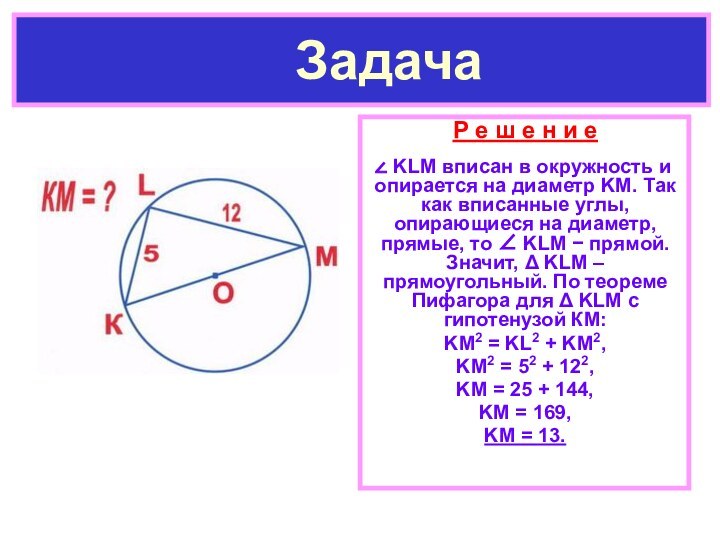
Задача
Р е ш е н и е
KLM
вписан в окружность и опирается на диаметр KM. Так
как вписанные углы, опирающиеся на диаметр, прямые, то ∠ KLM − прямой. Значит, Δ KLM – прямоугольный. По теореме Пифагора для Δ KLM с гипотенузой КМ:KM2 = KL2 + KM2,
KM2 = 52 + 122,
KM = 25 + 144,
KM = 169,
KM = 13.
Слайд 21 Не подлежит, однако, сомнению, что эту теорему знали
за много лет до Пифагора. Так, за 1500 лет
до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.
Слайд 22 Это же самое проделывалось тысячи лет назад при
строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и
в Мексике.Как свидетельствуют летописи, в Древнем Китае уже около 2200 года до н.э. для треугольника со сторонами 3, 4, 5 было найдено правило «гоу-гу», с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу, если известны оба катета.
Слайд 24 К теореме Пифагора его ученики составляли стишки,
вроде:
«Пифагоровы штаны
во все стороны равны»,
А также рисовали такие карикатуры:
Шарж
из учебника XVI века.Слайд 25 С глубокой древности математики находят все новые и
новые доказательства теоремы Пифагора, все новые и новые замыслы
ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса». Самостоятельное «открытие» доказательства теоремы Пифагора будет полезно и современным школьникам.Слайд 26 В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила
веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию
по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). Алтари по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.4
3
5
Слайд 27
Различные способы доказательства теоремы
Доказательства, основанные на использовании
понятия равновеликости фигур
Аддитивные доказательства (основаны на разложении квадратов, построенных
на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузеДоказательства методом достроения
Алгебраический метод доказательства
И т.д.
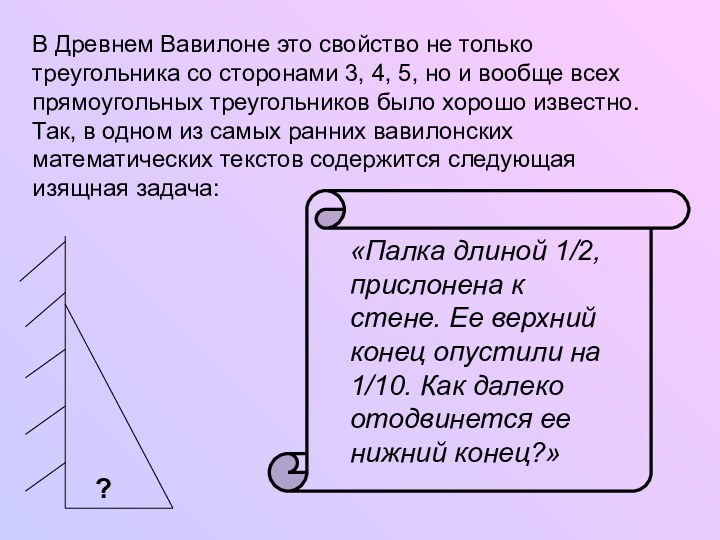
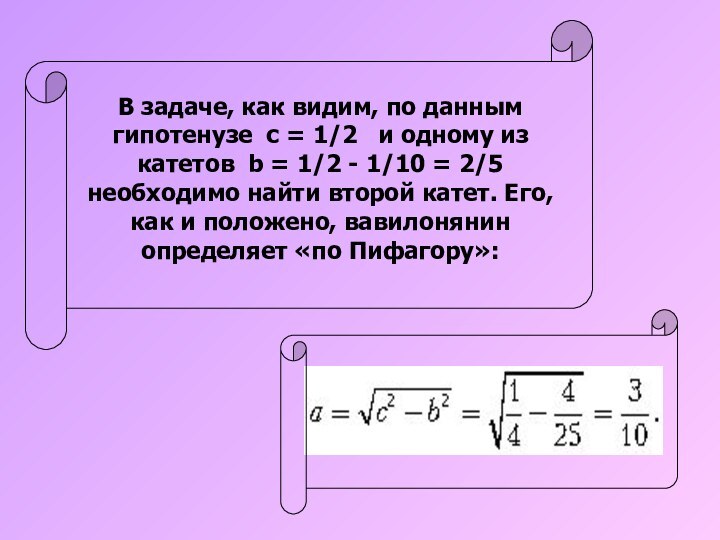
Слайд 28 В Древнем Вавилоне это свойство не только треугольника
со сторонами 3, 4, 5, но и вообще всех
прямоугольных треугольников было хорошо известно. Так, в одном из самых ранних вавилонских математических текстов содержится следующая изящная задача:Слайд 29 Среди многочисленных доказательств теоремы Пифагора методом разложения есть
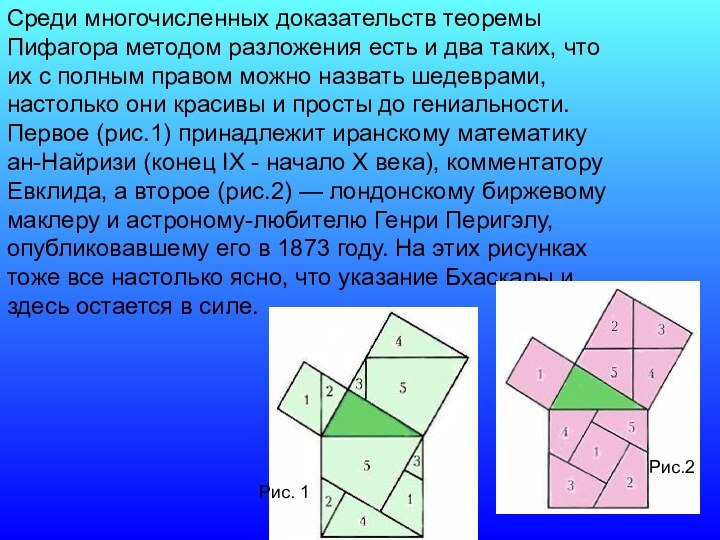
и два таких, что их с полным правом можно
назвать шедеврами, настолько они красивы и просты до гениальности. Первое (рис.1) принадлежит иранскому математику ан-Найризи (конец IX - начало Х века), комментатору Евклида, а второе (рис.2) — лондонскому биржевому маклеру и астроному-любителю Генри Перигэлу, опубликовавшему его в 1873 году. На этих рисунках тоже все настолько ясно, что указание Бхаскары и здесь остается в силе.Слайд 30 Большая часть доказательств теоремы Пифагора выполнена геометрическими методами,
среди которых значительное место занимает метод разложения. Сущность метода
разложения заключается в том, что квадрат, построенный на гипотенузе, с одной стороны, и квадраты, построенные на катетах, с другой, складываются из равных частей. Простейший пример применения этого метода имеем при доказательстве теоремы Пифагора для равнобедренного прямоугольного треугольника (см. рис.). Из этого рисунка все так понятно, что комментировать его не требуется. Как писал в подобных случаях индийский математик XII века Бхаскара: «Смотри!»
Слайд 31
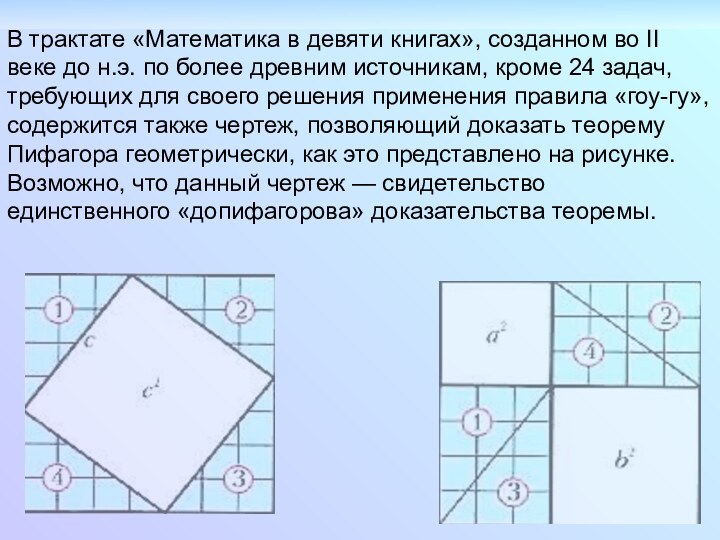
В трактате «Математика в девяти книгах», созданном во
II веке до н.э. по более древним источникам, кроме
24 задач, требующих для своего решения применения правила «гоу-гу», содержится также чертеж, позволяющий доказать теорему Пифагора геометрически, как это представлено на рисунке. Возможно, что данный чертеж — свидетельство единственного «допифагорова» доказательства теоремы.
Слайд 33
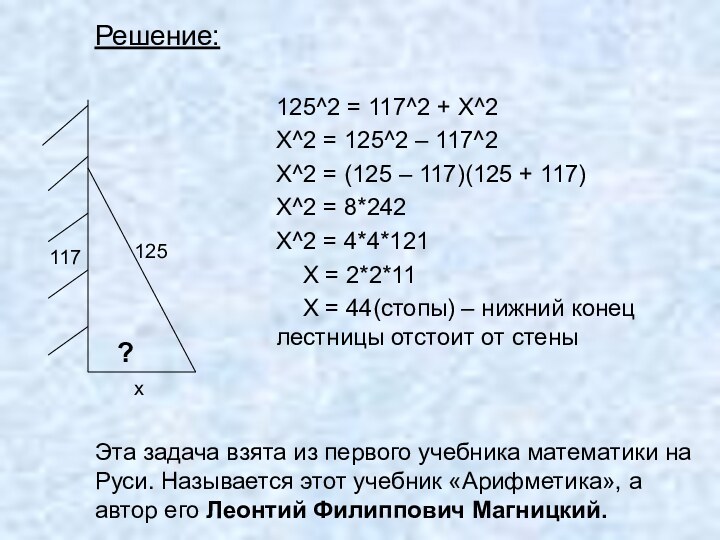
125^2 = 117^2 + Х^2
X^2 = 125^2 –
117^2
X^2 = (125 – 117)(125 + 117)
X^2 = 8*242
X^2
= 4*4*121X = 2*2*11
X = 44(стопы) – нижний конец лестницы отстоит от стены
Решение:
Эта задача взята из первого учебника математики на Руси. Называется этот учебник «Арифметика», а автор его Леонтий Филиппович Магницкий.
Слайд 34 Часто математики записывали свои задачи в стихотворной форме.
Вот одна из задач индийского математика XII века Бхаскары:
Слайд 36
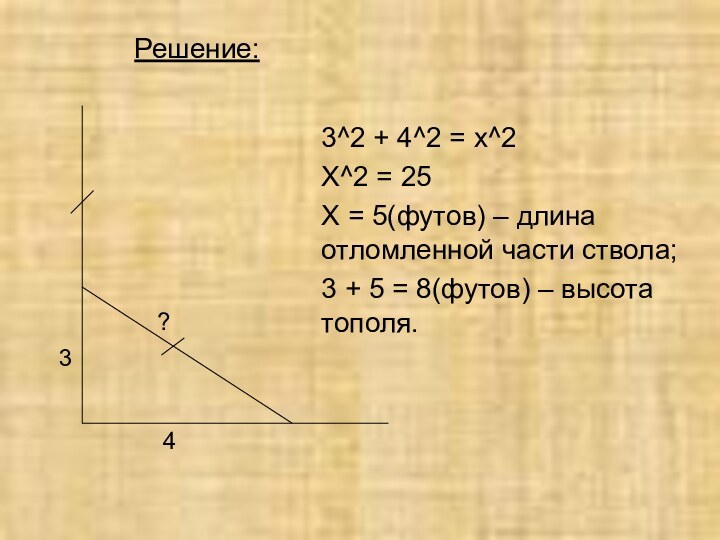
Решение:
3^2 + 4^2 = x^2
X^2 = 25
X =
5(футов) – длина отломленной части ствола;
3 + 5 =
8(футов) – высота тополя.Слайд 39 Сейчас теорему Пифагора знают практически все, кто когда-либо
изучал планиметрию.
Считается, что если мы хотим дать знать
внеземным цивилизациям о существовании разумной жизни на Земле, то следует посылать в космос изображение Пифагоровой фигуры. Так как если эту информацию смогут принять мыслящие существа, то они без сложной дешифровки сигнала поймут, что на земле существует достаточно развитая цивилизация.
Слайд 40
Источники информации:
www.1september.ru/ru
http://root/
И. Глейзер. История математики в школе.
//images.yandex.ru/yandsearch?
А.Д.Александров и
др. Геометрия 7-9
Атанасян и др. Геометрия 7-9
В.Н.Руденко, Г.А.Бахурин Геометрия
7-9В.Д.Чистяков. Старинные задачи по элементарной математике
Слайд 41
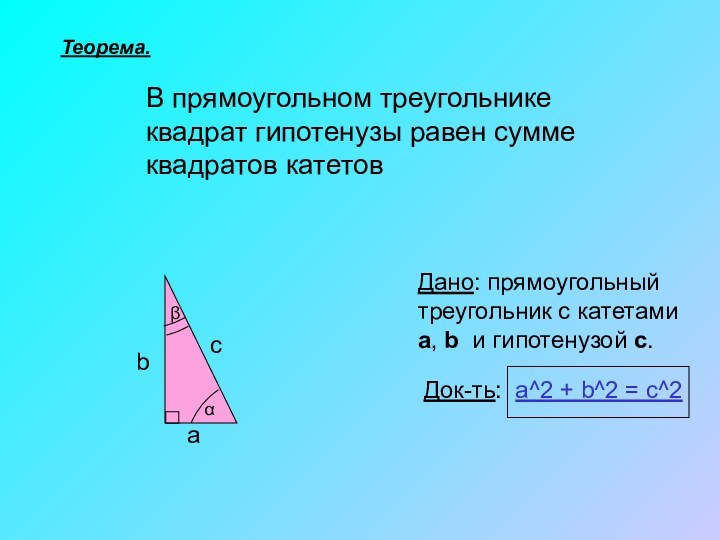
Теорема.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов
Дано: прямоугольный
треугольник с катетами a, b и гипотенузой c.
Док-ть:
a^2 + b^2 = c^2
Слайд 42
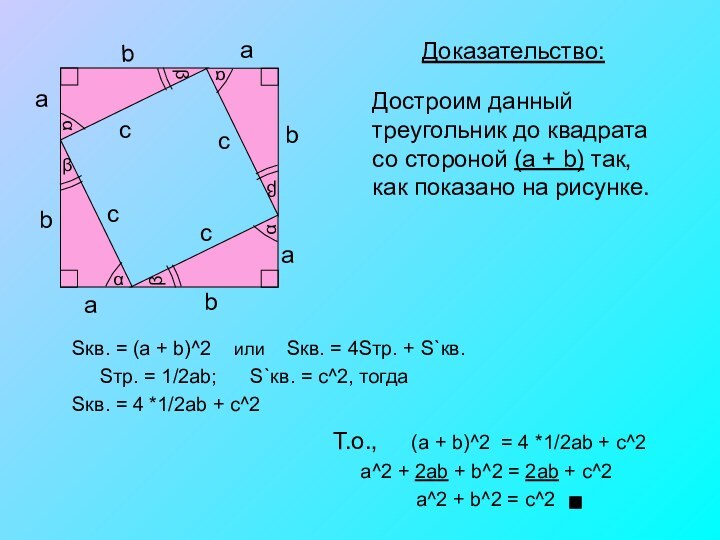
Доказательство:
Достроим данный треугольник до квадрата со стороной (a
+ b) так, как показано на рисунке.
Sкв. = (a
+ b)^2 или Sкв. = 4Sтр. + S`кв.Sтр. = 1/2ab; S`кв. = c^2, тогда
Sкв. = 4 *1/2ab + c^2
Т.о., (a + b)^2 = 4 *1/2ab + c^2
a^2 + 2ab + b^2 = 2ab + c^2
a^2 + b^2 = c^2
Слайд 43
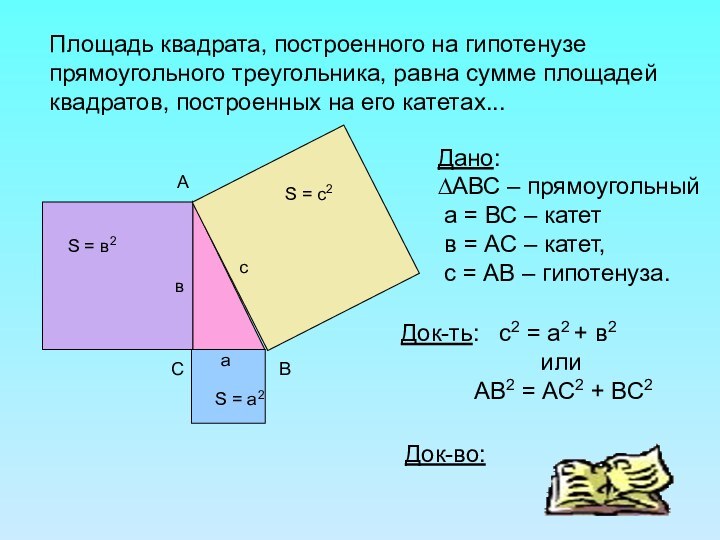
Дано:
∆АВС – прямоугольный
а = ВС –
катет
в = АС – катет,
с = АВ – гипотенуза.
A
B
C
с
S = c2
в
S = в2
a
S = a2
Док-ть: с2 = а2 + в2
или
АВ2 = АС2 + ВС2
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...
Док-во: