АВСD, если углы АВС и ВСD равны соответственно 30
и 120 градусов, а СD = 25.
25
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Решение геометрических задач в формате подготовки к ГИА
Содержание
- 2. Вариант 21 № 24. Найдите
- 3. Вариант 21 № 24. Найдите боковую сторону
- 4. Вариант 21 № 25. Точка Е –
- 5. Вариант 21 № 25. Точка Е –
- 6. Вариант 21. № 25. Точка Е –
- 7. Вариант 21 № 26 В треугольнике АВС
- 11. Вариант 23 № 24. Катеты прямоугольного треугольника
- 12. Вариант 23 № 25. Известно, что около
- 13. Вариант 23 № 26. На стороне ВС
- 14. Вариант 23 № 26. На стороне ВС
- 16. Вариант 29 № 25. Основания BC и
- 17. Вариант 29 № 26. Окружности радиусов 33
- 18. Вариант 29 № 26. Окружности радиусов 33
- 19. Вариант 29 № 26. Окружности радиусов 33
- 20. Вариант 29 № 26. Окружности радиусов 33
- 21. Вариант 29 № 26. Окружности радиусов 33
- 22. Вариант 13 № 24. Углы В и
- 23. Вариант 13 № 25. Окружности с центрами
- 24. Вариант 13 № 26. Биссектриса СМ треугольника
- 25. Вариант 13 № 26. Биссектриса СМ треугольника
- 26. Вариант 13 № 26. Биссектриса СМ треугольника
- 27. Вариант 19 № 25. В остроугольном треугольнике
- 28. Вариант 19 № 26. В треугольнике АВС
- 29. Скачать презентацию
- 30. Похожие презентации
Вариант 21 № 24. Найдите боковую сторону АВ трапеции АВСD, если углы АВС и ВСD равны соответственно 30 и 120 градусов, а СD = 25.
Слайд 3 Вариант 21 № 24. Найдите боковую сторону АВ трапеции
АВСD, если углы АВС и ВСD равны соответственно 30
и 120 градусов, а СD = 25.
25
Решение: Проведем высоты АН1 и СН2.
Найдем ∠ DCH2. ∠ DCH2 = 1200 -900 =300 .
Рассмотрим ΔDCH2. ∠СН2D =900 , значит ΔDCH2 прямоугольный.
Зная, что в прямоугольном треугольнике напротив угла 300 лежит катет равный половине гипотенузы, найдем DH2 = CD/2 = 25/2.
Найдем катет СН2 треугольника DCH2.
По теореме Пифагора,
СН22= CD2 – DH22 =
СН2 =
СН2 = АН1 как высоты. Δ АВН1 - прямоугольный.
∠АВН1 =300 , значит АВ = 2АН1 = 25√3.
Ответ: АВ = 25√3.
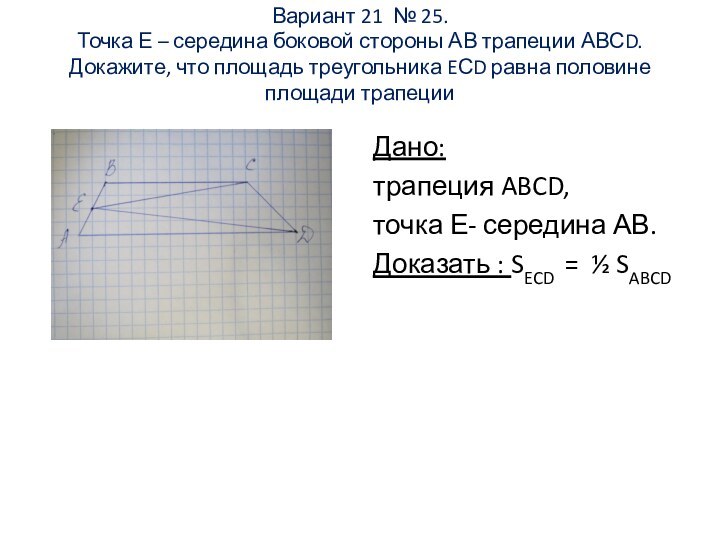
Слайд 4 Вариант 21 № 25. Точка Е – середина боковой
стороны АВ трапеции АВСD. Докажите, что площадь треугольника EСD
равна половине площади трапецииДано:
трапеция ABCD,
точка Е- середина АВ.
Доказать : SECD = ½ SABCD
Слайд 5 Вариант 21 № 25. Точка Е – середина боковой
стороны АВ трапеции АВСD. Докажите, что площадь треугольника EСD
равна половине площади трапецииДоказательство:
Проведем ЕН1 ┴ СВ и ЕН2 ┴АD.
Т.К. АD II BC, то точки Н1 , Е и Н2 лежат на одной прямой, значит Н1Н2 – высота трапеции АВСD.
Рассмотрим Δ ЕВН1 и Δ ЕАН2 . Они прямоугольные, т.к. ЕН1 ┴ СВ и ЕН2 ┴АD. АЕ = ЕВ, т.к. Е – середина АВ, ∠ЕВН1 = ∠ЕАН2 как внутренние накрест лежащие при ВСIIAD и секущей АВ. Значит Δ ЕВН1 = Δ ЕАН2 по гипотенузе и прилежащему к ней, острому углу.
Значит ЕН1 = ЕН2 . Значит ЕН1 = ЕН2 =1/2 Н1Н2.
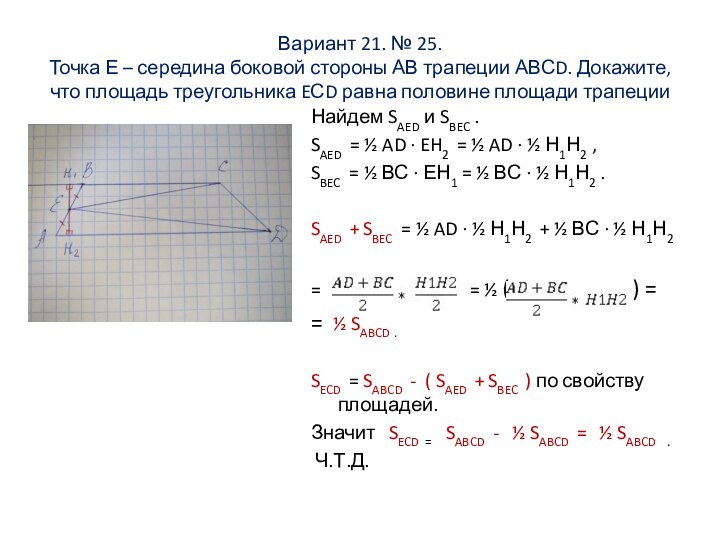
Слайд 6 Вариант 21. № 25. Точка Е – середина боковой
стороны АВ трапеции АВСD. Докажите, что площадь треугольника EСD
равна половине площади трапецииНайдем SAED и SBEC .
SAED = ½ AD · EH2 = ½ AD · ½ Н1Н2 ,
SBEC = ½ ВС · ЕН1 = ½ ВС · ½ Н1Н2 .
SAED + SBEC = ½ AD · ½ Н1Н2 + ½ ВС · ½ Н1Н2
= = ½ ( ) =
= ½ SABCD .
SECD = SABCD - ( SAED + SBEC ) по свойству площадей.
Значит SECD = SABCD - ½ SABCD = ½ SABCD .
Ч.Т.Д.
Слайд 7 Вариант 21 № 26 В треугольнике АВС биссектриса ВЕ
и медиана AD перпендикулярны и имеют одинаковую длину, равную
8. Найдите стороны треугольника АВС.Слайд 11 Вариант 23 № 24. Катеты прямоугольного треугольника равны 15
и 36. Найдите высоту, проведенную к гипотенузе.
Ответ: СН = 540/39Слайд 12 Вариант 23 № 25. Известно, что около четырехугольника АВСD
можно описать окружность и что продолжения сторон АD и
ВС четырехугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСD подобны.Слайд 13 Вариант 23 № 26. На стороне ВС остроугольного треугольника
АВС (АВ ≠ АС) как на диаметре построена полуокружность
, пересекающая высоту AD в точке М, AD = 49, МD = 42, Н - точка пересечения высот треугольника АВС. Найдите АН.Слайд 14 Вариант 23 № 26. На стороне ВС остроугольного треугольника
АВС (АВ ≠ АС) как на диаметре построена полуокружность
, пересекающая высоту AD в точке М, AD = 49, МD = 42, Н - точка пересечения высот треугольника АВС. Найдите АН.Слайд 16 Вариант 29 № 25. Основания BC и AD трапеции
ABCD равны соответственно 3 и 12, BD равно 6.
Докажите, что треугольники CBD и BDА подобны.Слайд 17 Вариант 29 № 26. Окружности радиусов 33 и 99
касаются внешним образом. Точки А и В лежат на
первой окружности, точки С и D на второй. При этом АС и BD – общие касательные окружностей. Найдите расстояние между АВ и СD.Слайд 18 Вариант 29 № 26. Окружности радиусов 33 и 99
касаются внешним образом. Точки А и В лежат на
первой окружности, точки С и D на второй. При этом АС и BD – общие касательные окружностей. Найдите расстояние между АВ и СD.Слайд 19 Вариант 29 № 26. Окружности радиусов 33 и 99
касаются внешним образом. Точки А и В лежат на
первой окружности, точки С и D на второй. При этом АС и BD – общие касательные окружностей. Найдите расстояние между АВ и СD.Слайд 20 Вариант 29 № 26. Окружности радиусов 33 и 99
касаются внешним образом. Точки А и В лежат на
первой окружности, точки С и D на второй. При этом АС и BD – общие касательные окружностей. Найдите расстояние между АВ и СD.Слайд 21 Вариант 29 № 26. Окружности радиусов 33 и 99
касаются внешним образом. Точки А и В лежат на
первой окружности, точки С и D на второй. При этом АС и BD – общие касательные окружностей. Найдите расстояние между АВ и СD.Слайд 22 Вариант 13 № 24. Углы В и С треугольника
АВС равны соответственно 71 и 79 градусов. Найдите ВС,
если радиус окружности, описанной около треугольника АВС, равен 8.
+
Слайд 23 Вариант 13 № 25. Окружности с центрами в точках
I и J пересекаются в точках А и В,
причем точки I и J лежат по одну сторона от прямой АВ. Докажите, что прямые АВ и IJ перпендикулярны.Слайд 24 Вариант 13 № 26. Биссектриса СМ треугольника АВС делит
сторону АВ на отрезки АМ = 5 и МВ
= 10. Касательная к описанной окружности треугольника АВС, проходящая через точку С, Пересекает прямую АВ точке D. Найдите СD.Слайд 25 Вариант 13 № 26. Биссектриса СМ треугольника АВС делит
сторону АВ на отрезки АМ = 5 и МВ
= 10. Касательная к описанной окружности треугольника АВС, проходящая через точку С, Пересекает прямую АВ точке D. Найдите СD.Слайд 26 Вариант 13 № 26. Биссектриса СМ треугольника АВС делит
сторону АВ на отрезки АМ = 5 и МВ
= 10. Касательная к описанной окружности треугольника АВС, проходящая через точку С, Пересекает прямую АВ точке D. Найдите СD.Слайд 27 Вариант 19 № 25. В остроугольном треугольнике АВС проведены
высоты ВВ1 и СС1. Докажите, что углы ВВ1С1 и
ВСС1 равны.Слайд 28 Вариант 19 № 26. В треугольнике АВС биссектриса угла
