- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Центральная и осевая симметрия
Содержание
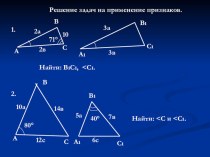
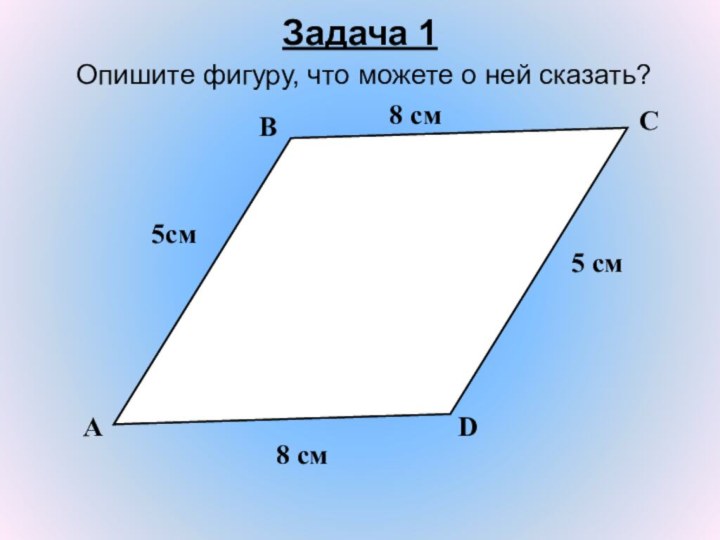
- 2. Повторение пройденного
- 3. Задача 1 Опишите фигуру, что можете о ней сказать? АВСD5cм5 см8 см8 см
- 4. Задача 2 Угол между диагоналями прямоугольника
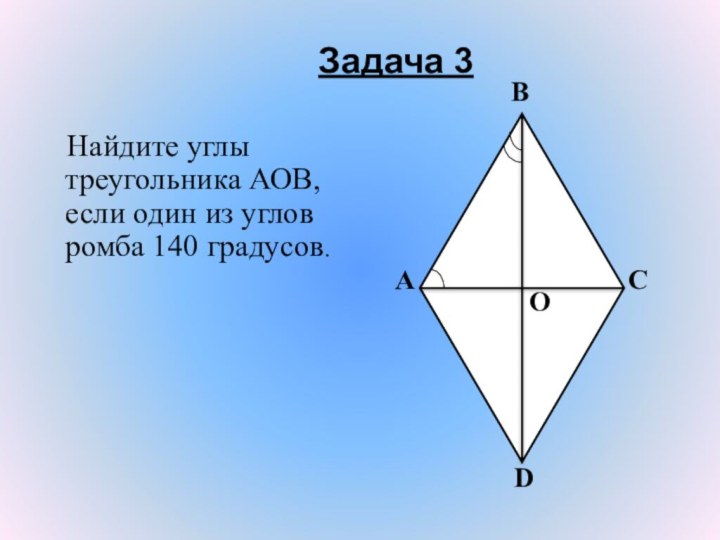
- 5. Задача 3 Найдите углы треугольника АОВ, если один из углов ромба 140 градусов. D
- 6. Задача 4Точка О середина АС и середина
- 7. Как много В нашем мире красоты, Которой,
- 8. Но, можно ли всё это объяснить? И что подскажут в этом нам науки?
- 9. Что Вас привлекло в этих фотографиях?
- 10. Тема занятияЦентральная и осевая симметрия
- 11. Сегодня на занятииСформулировать понятия центральной и осевой
- 12. Вейль ГерманВейль Герман (9.11.1885— 8.12.1955) - немецкий
- 13. Что такое симметрия «Симметрия является той
- 14. Что такое симметрия«Словарь С.И. Ожегова»: «Симметрия -
- 15. Симметричность точек относительно прямой A1AaOОпределение Две
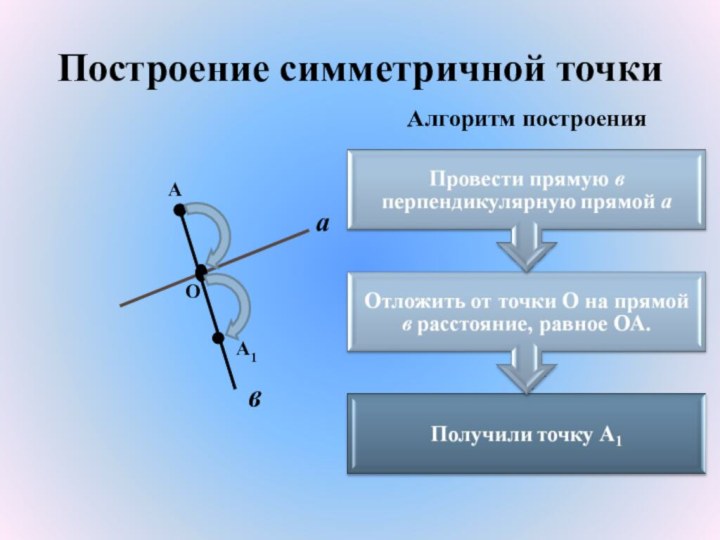
- 16. Построение симметричной точкиАаА1ОвАлгоритм построения
- 17. Задание №1K1
- 18. Симметричность фигуры относительно прямойaОпределениеФигура называется симметричной относительно
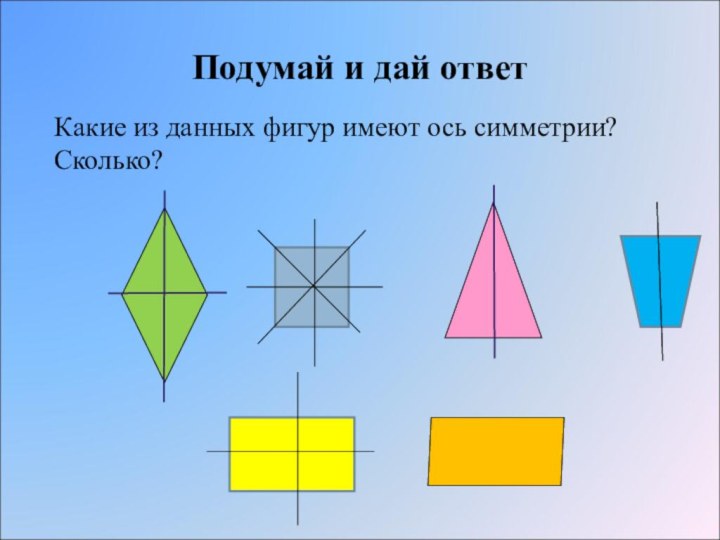
- 19. Подумай и дай ответ Какие из данных фигур имеют ось симметрии? Сколько?
- 20. Симметричность точек относительно центра
- 21. Построение симметричной точкиАОА1Алгоритм построения
- 22. Симметричность фигуры относительно центра
- 23. Подумай и дай ответ
- 24. Подумай и дай ответ
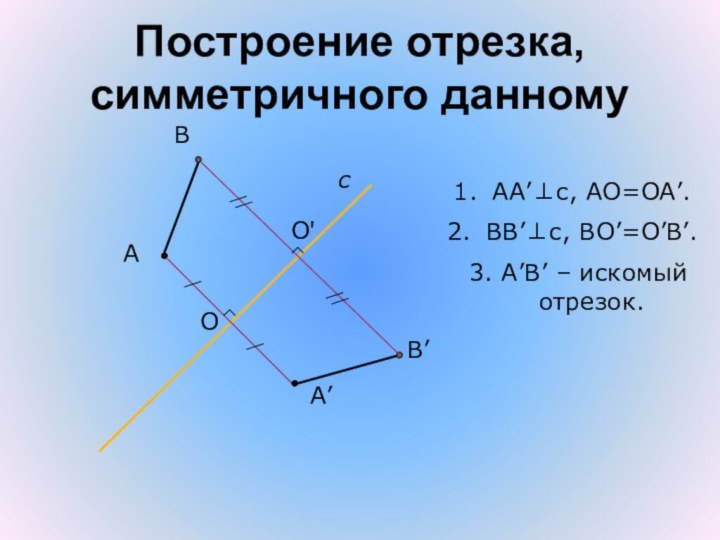
- 25. Построение отрезка, симметричного данномуАсА’ВВ’OO'АА’⊥с, АО=ОА’.ВВ’⊥с, ВО’=О’В’.3. А’В’ – искомый отрезок.
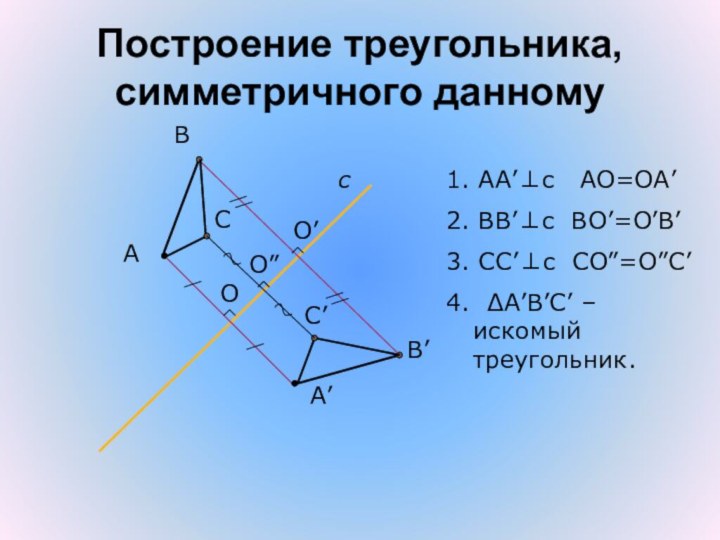
- 26. Построение треугольника, симметричного данномуАсА’ВВ’СС’1. AA’⊥c AO=OA’2. BB’⊥c BO’=O’B’3. СС’⊥c СO”=O”С’4. ΔA’B’С’ – искомый треугольник.OO”O’
- 27. Будут ли симметричны относительно х=0 следующие множества
- 28. Будут ли симметричны относительно х=1 следующие множества (-1;3), (-2;4], (-1;0)U(2;3), (-5;7)
- 30. Симметрия в мире растенийОсевая симметрия наблюдается у
- 31. Симметрия в мире растенийДля цветов в большей степени характерна поворотная симметрия.
- 32. Симметрия в мире насекомых, рыб, птиц, животныхОсевая симметрия хорошо видна у бабочек, некоторых видов птиц, насекомых.
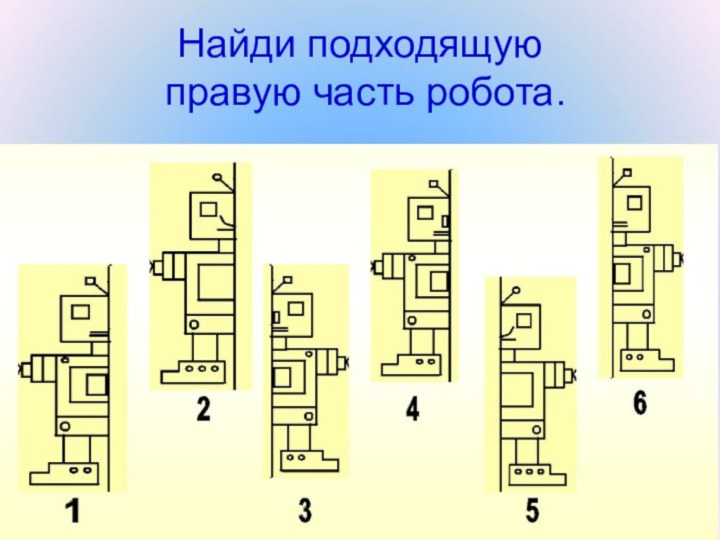
- 33. Найди подходящую правую часть робота.
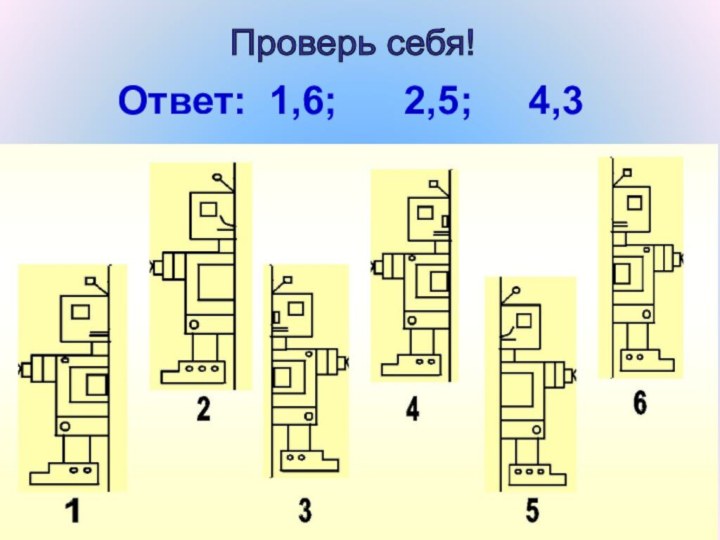
- 34. Проверь себя! Ответ: 1,6; 2,5; 4,3
- 35. Скачать презентацию
- 36. Похожие презентации
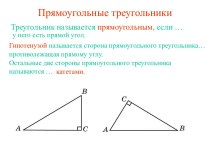
Повторение пройденного














![Презентация по математике на тему Центральная и осевая симметрия Будут ли симметричны относительно х=0 следующие множества [-3;3], (-2;2],](/img/tmb/7/664109/746064b0489dcd13626577a1f4324e24-720x.jpg)
![Презентация по математике на тему Центральная и осевая симметрия Будут ли симметричны относительно х=1 следующие множества (-1;3), (-2;4], (-1;0)U(2;3), (-5;7)](/img/tmb/7/664109/9011e2689db2dccbc026b9c7133c2801-720x.jpg)





Слайд 4
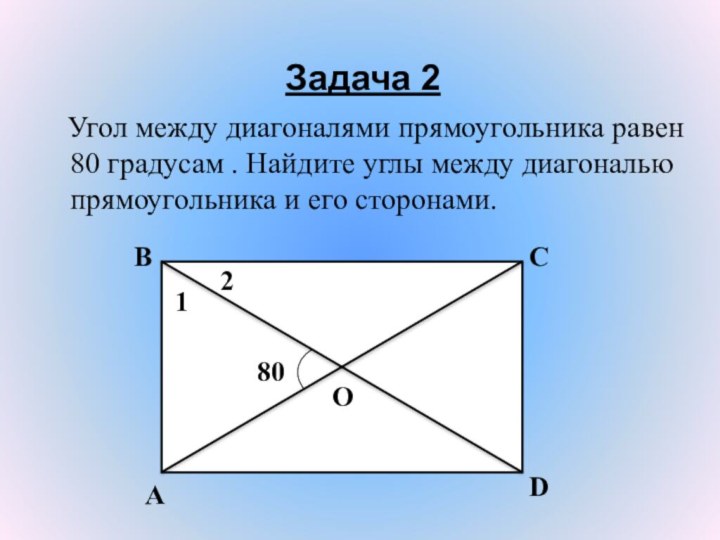
Задача 2
Угол между диагоналями прямоугольника равен
80 градусам . Найдите углы между диагональю прямоугольника и
его сторонами.
Слайд 6
Задача 4
Точка О середина АС и середина ВD.
Что можно сказать о четырехугольнике АВСD?
АВСD- параллелограмм
Точка
О середина АС и середина ВD и диагонали равны.АВСD- прямоугольник
Точка О середина АС и середина ВD. Диагонали равны и взаимно перпендикулярны.
АВСD- квадрат
Слайд 7
Как много
В нашем мире красоты,
Которой, часто
мы не замечаем.
Все потому,
Что каждый день встречаем
Её давно знакомые черты.
Мы знаем,
Что красивы облака,
Река, цветы,
Лицо любимой мамы,
И Пушкина, летящая строка,
И то,
Что человек
Красив делами…
Слайд 11
Сегодня на занятии
Сформулировать понятия центральной и осевой симметрии,
симметричной фигуры.
Рассмотреть какими видами симметрии обладают известные нам
геометрические фигуры. Научиться строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией.
Слайд 12
Вейль Герман
Вейль Герман (9.11.1885— 8.12.1955) - немецкий математик.
Окончил Гёттингенский университ. В 1913—1930г. профессор Цюрихского политехнического института,
в 1930—33 профессор Гёттингенского университета, в 1933 эмигрировал в США.
Слайд 13
Что такое симметрия
«Симметрия является той идеей,
с помощью которой человек веками пытается объяснить и создать
порядок, красоту и совершенство»Герман Вейль
Слайд 14
Что такое симметрия
«Словарь С.И. Ожегова»: «Симметрия - соразмерность,
пропорциональность частей чего-нибудь, расположенных по обе стороны от середины,
центра».«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
Слайд 15
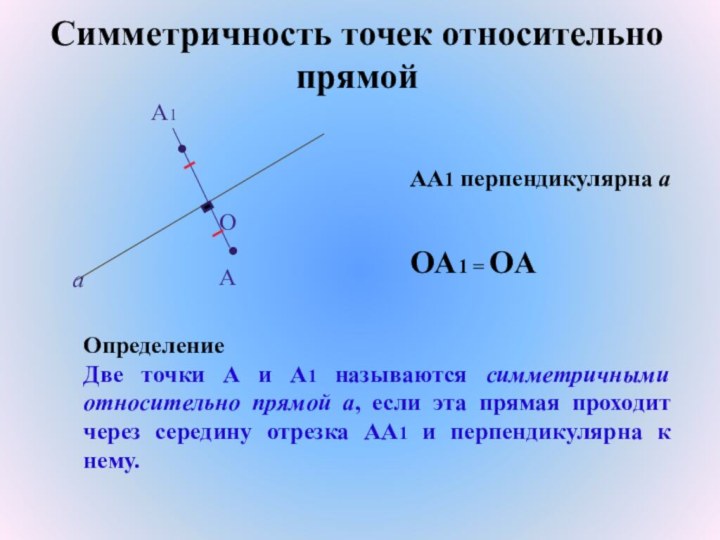
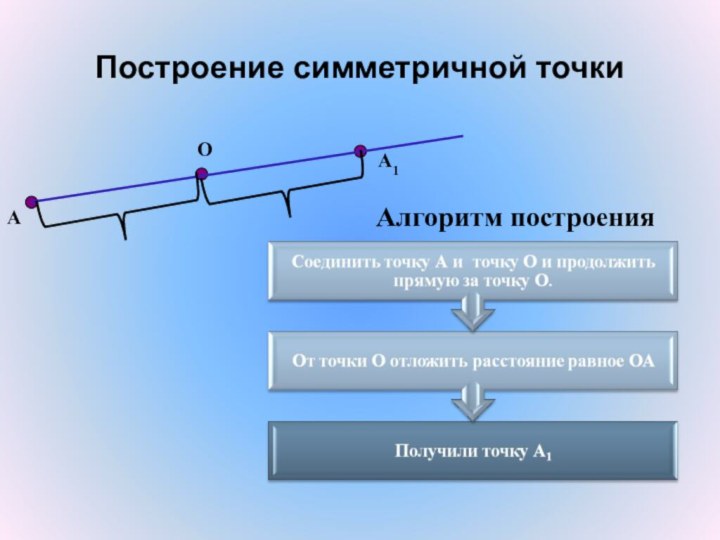
Симметричность точек относительно прямой
A1
A
a
O
Определение
Две
точки А и А1 называются симметричными относительно прямой а,
если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
АА1 перпендикулярна а
OА1 = OA
Слайд 18
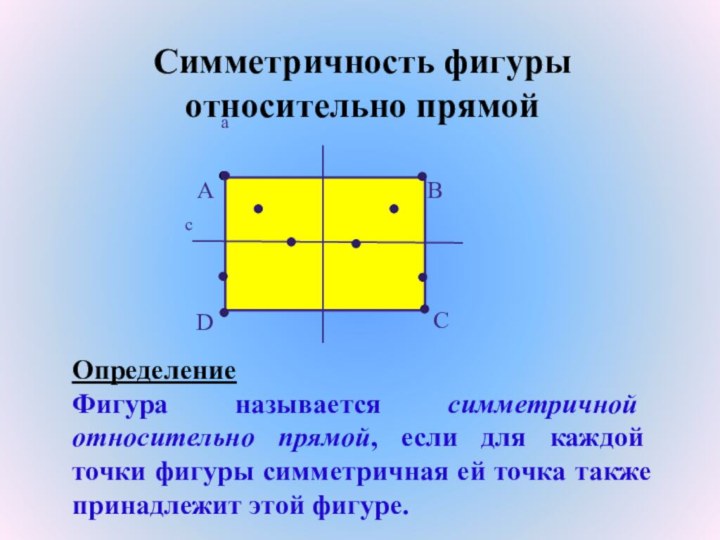
Симметричность фигуры относительно прямой
a
Определение
Фигура называется симметричной относительно прямой,
если для каждой точки фигуры симметричная ей точка также
принадлежит этой фигуре.
Слайд 20
Симметричность точек относительно центра
ОА1 = ОА
A
O
A1
Определение
Точки A и A1 называются симметричными относительно
точки О, если О – середина отрезка AA1.
Слайд 22
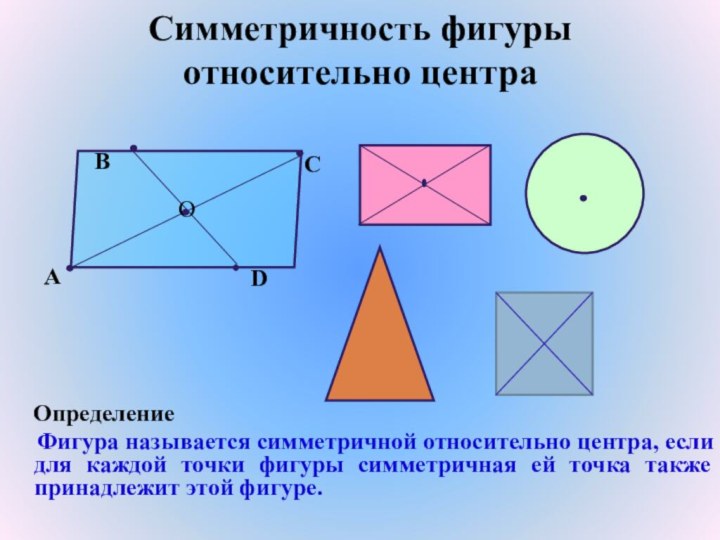
Симметричность фигуры относительно центра
Определение
Фигура называется симметричной относительно центра, если
для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.A
B
C
D
O