- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пропорциональность
Содержание
- 2. «Высшее назначение математики состоит в том,
- 3. «... Геометрия
- 4. Прямоугольный треугольник с соотношением сторон 3:4:5. Сумма
- 5. ЗемледелиеОтношение 3:4:5
- 6. Моделирование Современный модельный бизнес также использует идеальные пропорции.
- 7. Леонардо Да Винчи ввел
- 8. Леонардо да Винчи, Рафаэль, Микеланджело и Виньола
- 9. Золотым сечением и даже «божественной
- 10. Золотой треугольник АВС Золотым называется такой равнобедренный
- 11. Золотая пропорцияДано: отрезок АВ.
- 12. Построение. Построим прямоугольный треугольник, у которого один
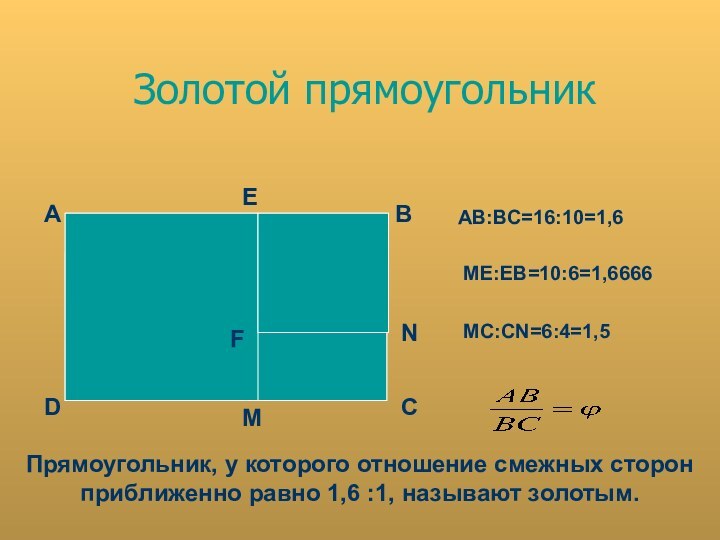
- 13. Золотой прямоугольникFАВСEDNMАВ:ВС=16:10=1,6ME:EB=10:6=1,6666MC:СN=6:4=1,5Прямоугольник, у которого отношение смежных сторон приближенно равно 1,6 :1, называют золотым.
- 14. Построение.Построить прямоугольник АВСD, стороны которого 16 и
- 15. Архитектура
- 16. Леонардо Фибоначчи разгадал тайну числаРяд чисел выглядит
- 17. Построение спирали:
- 18. Раковина в форме спирали заинтересовала
- 19. С помощью числового ряда Фибоначчи описывается устройство Галактик, волн
- 20. Млечный путь - так называется
- 21. Последовательность Фибоначчи, проиллюстрированная природой.
- 22. Семена в подсолнухе, в шишке
- 23. Все живое подчиняется божественному закону
- 24. И нерукотворные творения
- 25. Скачать презентацию
- 26. Похожие презентации
«Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает.»























Слайд 3 «... Геометрия владеет
двумя сокровищами - теоремой Пифагора и золотым сечением, и
если первое из них можно сравнить с мерой золота, то второе - с драгоценным камнем...».Иоганн Кеплер
Слайд 4
Прямоугольный треугольник
с соотношением сторон 3:4:5.
Сумма указанных
чисел (3+4+5=12)
с древних времен использовалась
как единица кратности.
Египетский
треугольник
Слайд 5
Земледелие
Отношение 3:4:5
было использовано при построении
прямых углов с помощью веревки,
размеченной узлами
на
3/12 и 7/12 ее длины.
Слайд 7 Леонардо Да Винчи ввел термин
«золотое сечение», он говорил: «Пусть никто, не будучи математиком,
не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.Слайд 8 Леонардо да Винчи, Рафаэль, Микеланджело и Виньола размышляли
о законах «науки пространства», искали тот самый закон Числа,
который зовется золотой пропорцией Слайд 9 Золотым сечением и даже «божественной пропорцией»
называют такое пропорциональное деление отрезка на неравные части, при
котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всемуa : b = b : c
Слайд 10
Золотой треугольник
А
В
С
Золотым называется такой равнобедренный треугольник, основание
и боковая сторона
которого находятся
в золотом отношении:
Золотой треугольник
Буква
ϕ (фи) – первая буква в имени великого Фидия, который, по преданию, часто использовалзолотое сечение в своих скульптурах.
Слайд 11
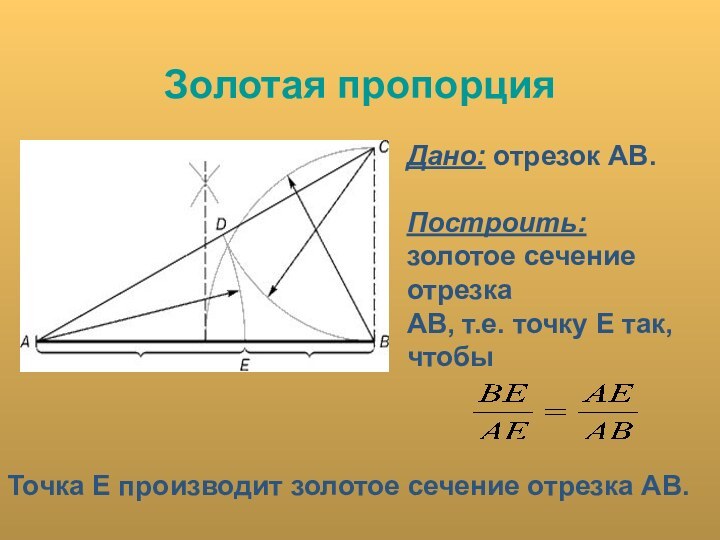
Золотая пропорция
Дано: отрезок АВ.
Построить:
золотое сечение отрезка АВ, т.е. точку Е так, чтобы
.
Точка Е производит золотое сечение отрезка АВ.
Слайд 12
Построение.
Построим прямоугольный треугольник, у которого один катет
в два раза больше другого. Для этого восстановим в
точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС=1/2 АВ.Далее, соединим точки А и С, отложим отрезок CD=CB, и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Слайд 13
Золотой прямоугольник
F
А
В
С
E
D
N
M
АВ:ВС=16:10=1,6
ME:EB=10:6=1,6666
MC:СN=6:4=1,5
Прямоугольник, у которого отношение смежных сторон
приближенно
равно 1,6 :1, называют золотым.
Слайд 14
Построение.
Построить прямоугольник АВСD, стороны которого 16 и 10.
Найти отношение сторон.
На сторонах прямоугольника построить квадрат АEМD наибольшей
площади.Измерить стороны прямоугольника ВСМЕ. Найти отношение сторон.
На сторонах прямоугольника ВСМЕ построить квадрат FNBE наибольшей площади.
Измерить стороны прямоугольника FNCM. Найти отношение сторон.
Сравнить числа, показывающие отношениz длин сторон прямоугольников, сделать вывод.
Слайд 16
Леонардо Фибоначчи разгадал тайну числа
Ряд чисел выглядит так:
0, 1, 1, 2, 3, 5, 8, 13,
21, 34, 55…Его особенность заключается в следующем – каждое число в ряду, начиная с третьего, складывается из суммы двух предшествующих: 2+3=5
3 + 5 = 8
5 + 8 = 13 и т.д.
При этом отношение соседних чисел стремится к золотому сечению:
21 : 34 = 0,617
34 : 55 = 0,618
Слайд 17
Построение спирали:
0,
1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, 144…Ряд Фибоначчи – это не только математическая загадка, мы встречаемся с ним каждый день в повседневной жизни:
Слайд 18 Раковина в форме спирали заинтересовала
и Архимеда: он выяснил, что увеличение длины завитков раковины
– постоянная величина, равная 1,618.
Слайд 20
Млечный путь -
так называется
наша галактика
В самом центре есть большая чёрная дыра, но
это предположение. Мы можем видеть нашу галактику, только с ребра. В галактике млечный путь, примерно двести миллиардов звёзд, расположенных по спирали, вокруг «чёрной дыры».Размеры галактики млечный путь – двадцать тысяч световых лет в ширину и сто тысяч в длину.