Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Перпендикуляр к прямой (7 класс)

Содержание

Дано: Δ ADC, Δ ABC, AD=AB, ∠1= ∠2, ∠ABC=108°, ∠ACB=32° Доказать: Δ ADC=Δ ABC, найти ∠ADC, ∠ACD Доказательство:ADCB12
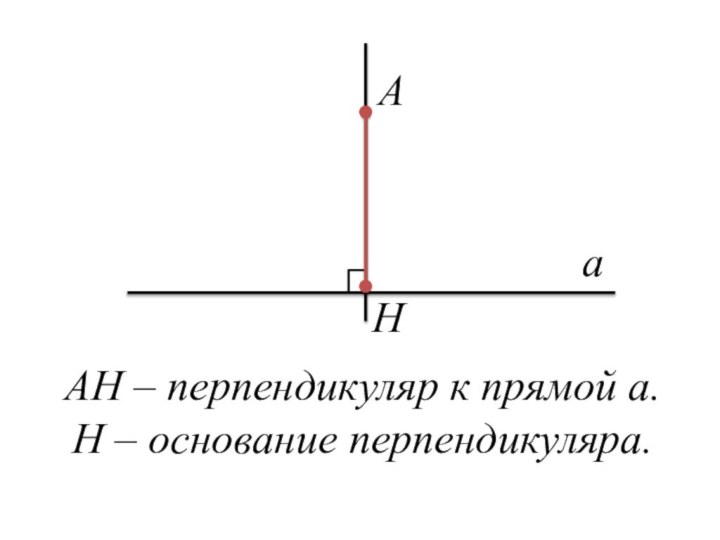
Домашнее задание§2, п.16, теорему и доказательство наизусть, доказательство записать в тетрадь.№ 100, Дано: Δ ADC, Δ ABC, AD=AB, ∠1= ∠2, ∠ABC=108°, ∠ACB=32° Доказать: AD=AB, ∠1= ∠2 (по условию задачи), сторона АС – общая, отсюда Δ Дано: Δ ADC, Δ ABC, DC=AB, ∠3= ∠4, ∠ABC=102°, ∠ACB=38° Доказать: AB=DC, ∠4= ∠3 (по условию задачи), сторона АС – общая, отсюда Δ 05.11. Классная работа Тема: Перпендикуляр к прямой. AHaAH – перпендикуляр к прямой а.Н – основание перпендикуляра. 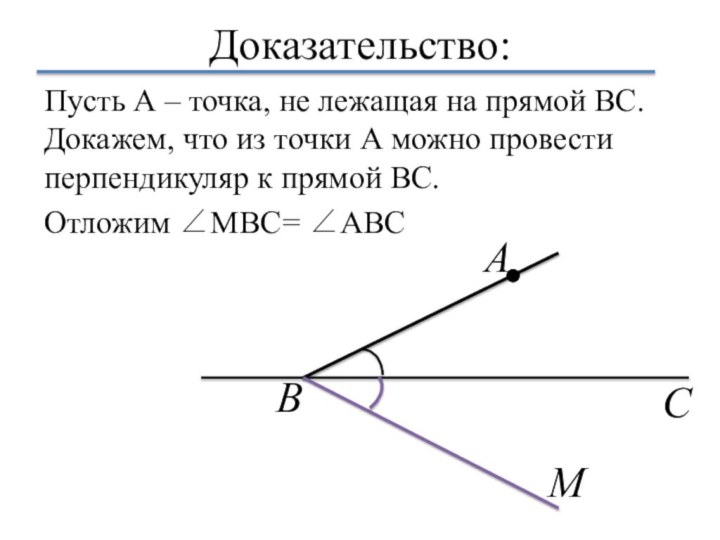ТеоремаИз точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.ABC Доказательство:Пусть А – точка, не лежащая на прямой BC. Докажем, что из Т.к. ∠MBC= ∠ABC наложим их друг на друга.Сторона ВА и ВМ совместятся, Докажем, что из точки А можно провести только один перпендикуляр к прямой
Слайды презентации

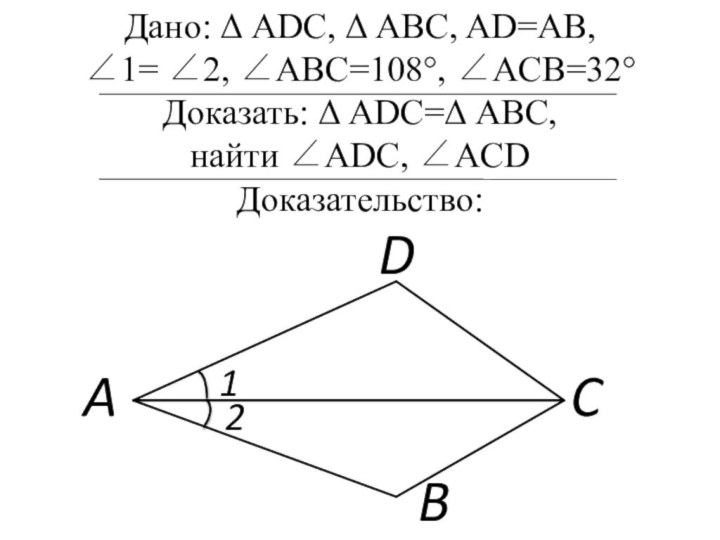
Слайд 2 Дано: Δ ADC, Δ ABC, AD=AB, ∠1= ∠2,

Дано: Δ ADC, Δ ABC, AD=AB, ∠1= ∠2, ∠ABC=108°, ∠ACB=32° Доказать:

∠ABC=108°, ∠ACB=32° Доказать: Δ ADC=Δ ABC, найти ∠ADC, ∠ACD Доказательство:
A
D
C
B
1
2

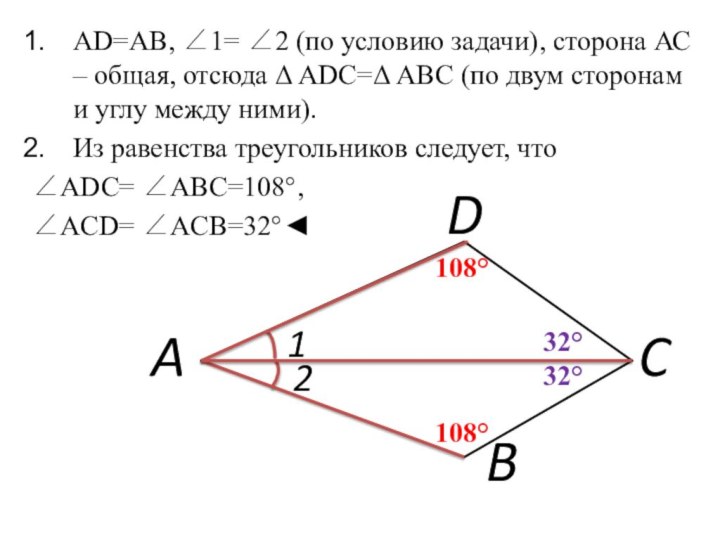
Слайд 3 AD=AB, ∠1= ∠2 (по условию задачи), сторона АС

AD=AB, ∠1= ∠2 (по условию задачи), сторона АС – общая, отсюда

– общая, отсюда Δ ADC=Δ ABC (по двум сторонам

и углу между ними).
Из равенства треугольников следует, что
∠ADC= ∠ABC=108°,
∠ACD= ∠ACB=32°◄

A

D

C

B

1

2

108°

108°

32°

32°

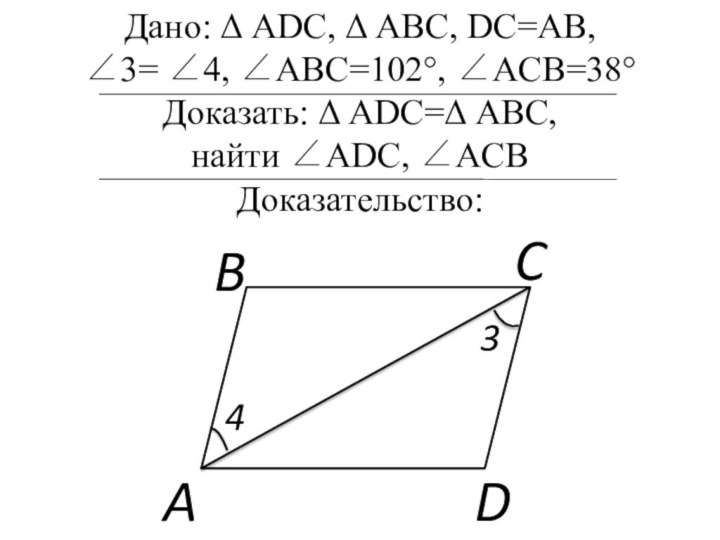
Слайд 4 Дано: Δ ADC, Δ ABC, DC=AB, ∠3= ∠4,

Дано: Δ ADC, Δ ABC, DC=AB, ∠3= ∠4, ∠ABC=102°, ∠ACB=38° Доказать:

∠ABC=102°, ∠ACB=38° Доказать: Δ ADC=Δ ABC, найти ∠ADC, ∠ACB Доказательство:
A
D
C
B
4
3

Слайд 5 AB=DC, ∠4= ∠3 (по условию задачи), сторона АС

AB=DC, ∠4= ∠3 (по условию задачи), сторона АС – общая, отсюда

– общая, отсюда Δ ADC=Δ ABC (по двум сторонам

и углу между ними).
Из равенства треугольников следует, что
∠BCA= ∠ACB=38°,
∠ABC= ∠ADC=102°◄

A

D

C

B

4

3

38°

102°

102°

Слайд 6 05.11. Классная работа


Тема: Перпендикуляр к прямой.

05.11. Классная работа Тема: Перпендикуляр к прямой.

Слайд 7 A
H
a
AH – перпендикуляр к прямой а.
Н – основание

AHaAH – перпендикуляр к прямой а.Н – основание перпендикуляра.

перпендикуляра.

Слайд 8 Теорема
Из точки, не лежащей на прямой, можно провести

ТеоремаИз точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.ABC

перпендикуляр к этой прямой, и притом только один.
A
B
C

Слайд 9 Доказательство:
Пусть А – точка, не лежащая на прямой

Доказательство:Пусть А – точка, не лежащая на прямой BC. Докажем, что

BC. Докажем, что из точки А можно провести перпендикуляр

к прямой ВС.
Отложим ∠MBC= ∠ABC

A

B

C

M

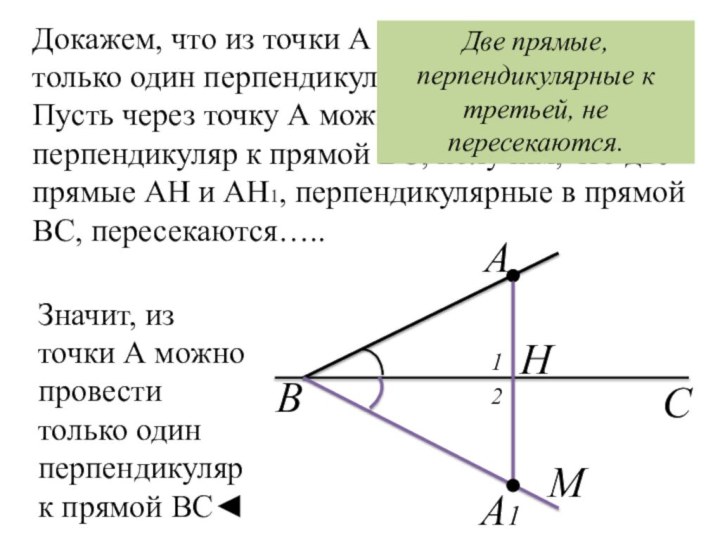
Слайд 10 Т.к. ∠MBC= ∠ABC наложим их друг на друга.
Сторона

Т.к. ∠MBC= ∠ABC наложим их друг на друга.Сторона ВА и ВМ

ВА и ВМ совместятся, как и сторона ВС. При

этом точка А наложится на точку А1 луча ВМ.
Обозначим Н – как точку пересечения прямых АА1 и ВС. Получим ∠1 и ∠2
совместятся. Следовательно,
∠1=∠2. Но углы 1 и 2 –
смежные, значит,
каждый из них
прямой.
Итак, АН┴ВС.

A

B

C

M

A1

Н

1

2

  • Имя файла: prezentatsiya-po-geometrii-na-temu-perpendikulyar-k-pryamoy-7-klass.pptx
  • Количество просмотров: 176
  • Количество скачиваний: 0
- Предыдущая Презентация для педагогов Нравственно-патриотическое воспитание в ДОУ № 26
Следующая - Окр. мир. Весна идет.

Похожие презентации

Презентация по геометрии на тему Правильные многоугольники (9 класс) Презентация по геометрии на тему Правильные многоугольники (9 класс) 152
Длина отрезка Длина отрезка 180
Выпуклые многогранные углы Выпуклые многогранные углы 204
Презентация по геометрии на тему Векторы (8 класс) Презентация по геометрии на тему Векторы (8 класс) 145
Свойства равнобедренного треугольника Свойства равнобедренного треугольника 146
Геометрические формы в разных архитектурных стилях Геометрические формы в разных архитектурных стилях 179
Презентация к уроку на тему пирамиды. немного истории Презентация к уроку на тему пирамиды. немного истории 173
Презентация по математике на тему Тела вращения. Шар. Сечения шара. Взаимное расположение сферы и плоскости (10-11 классы) Презентация по математике на тему Тела вращения. Шар. Сечения шара. Взаимное расположение сферы и плоскости (10-11 классы) 202
Откладывание вектора от данной точки Откладывание вектора от данной точки 198
Презентация Рельеф Южной Америки Презентация Рельеф Южной Америки 167
Что такое геометрия Что такое геометрия 139
Средняя линия треугольника Средняя линия треугольника 179
Аксиомы стереометрии Аксиомы стереометрии 135
Высота Высота 179
Третий признак равенства треугольников Третий признак равенства треугольников 157
Как найти площадь многоугольника Как найти площадь многоугольника 151
Комбинации геометрических тел Комбинации геометрических тел 161
Цилиндр Цилиндр 168
Презентация по математике на тему Пропорциональные отрезки-8 кл. Презентация по математике на тему Пропорциональные отрезки-8 кл. 158
Современная архитектура и геометрия. Настольный буклет Современная архитектура и геометрия. Настольный буклет 188
Презентация по геометрии Решение задач Презентация по геометрии Решение задач 127
Многоугольники Многоугольники 149
Площадь криволинейной трапеции и интеграл Площадь криволинейной трапеции и интеграл 153
Построение сечений параллелепипеда Построение сечений параллелепипеда 158
Презентация по геометрии для 9 класса по теме Движение. Презентация по геометрии для 9 класса по теме Движение. 164
Презентация по математике на тему Призма, виды призм. Презентация по математике на тему Призма, виды призм. 182
Старинные задачи Старинные задачи 185
Окружность в аксонометрии Окружность в аксонометрии 166
Основы геометрии Основы геометрии 198
Векторы 8 класс Векторы 8 класс 278