- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Преобразование фигур. Обратное преобразование. Определение и свойства гомотетии.
Содержание
- 2. На этом уроке вы узнаете, что такое
- 3. В ходе урока вам понадобится знание терминологии на трёх языках.
- 4. ЗаданиеСейчас откроется таблица с терминами по теме
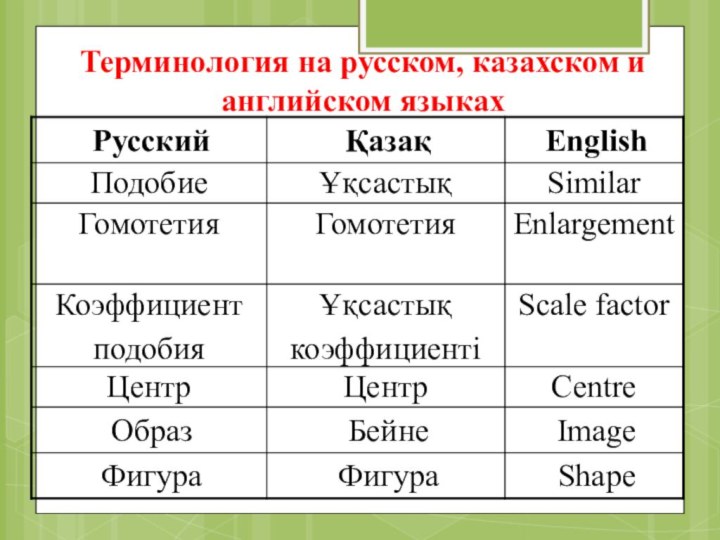
- 5. Терминология на русском, казахском и английском языках
- 6. «Восстановите невидимое» Запишите термины, которые вы запомнили
- 7. Даурен стоит на набережной реки
- 8. Гомотетия – одно из важнейших преобразований подобия.
- 9. Подобие фигур Преобразование плоскости, при котором
- 10. Свойства подобияСвойство 1. Подобие переводит отрезки в
- 11. Преобразование плоскости или пространства, при котором
- 12. В отличие от гомотетии, геометрические преобразования
- 13. Если фигура F преобразуется в результате гомотетии
- 14. Свойства гомотетии с коэффициентом k.Прямая
- 15. Гомотетичные окружности Всякая гомотетия отображает окружность на окружность,
- 16. Чтобы гомотетия
- 17. FF1Пусть F – данная фигура, О –
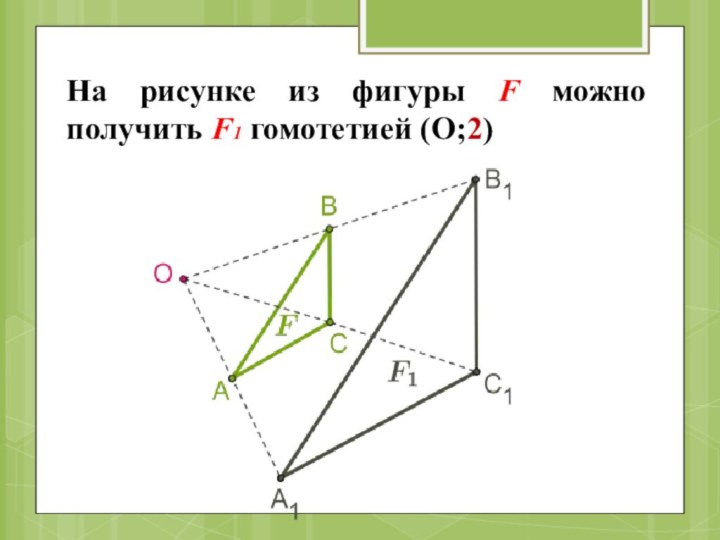
- 18. На рисунке из фигуры F можно получить F1 гомотетией (О;2)
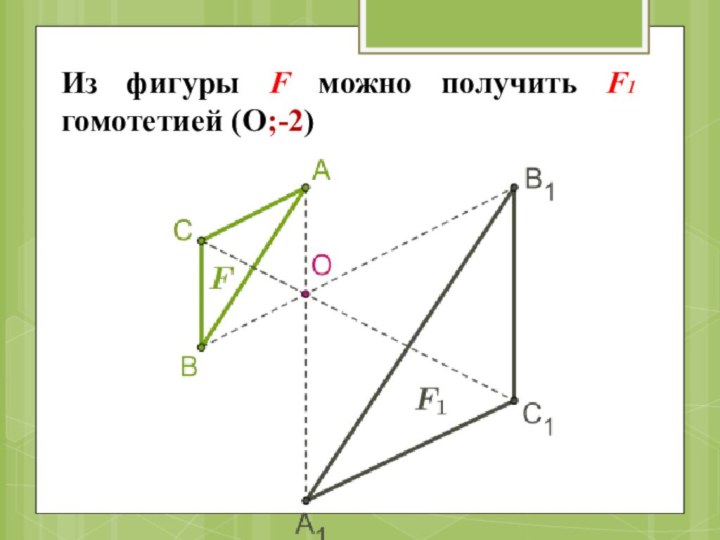
- 19. Из фигуры F можно получить F1 гомотетией (О;-2)
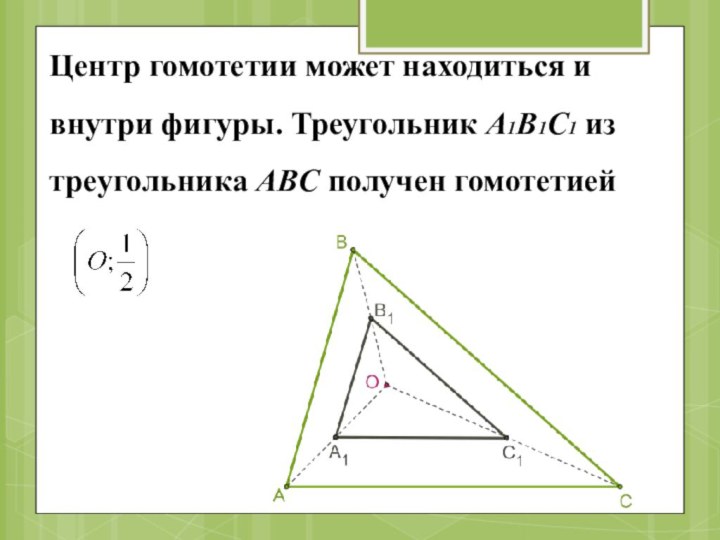
- 20. Центр гомотетии может находиться и внутри фигуры. Треугольник A1B1C1 из треугольника ABC получен гомотетией
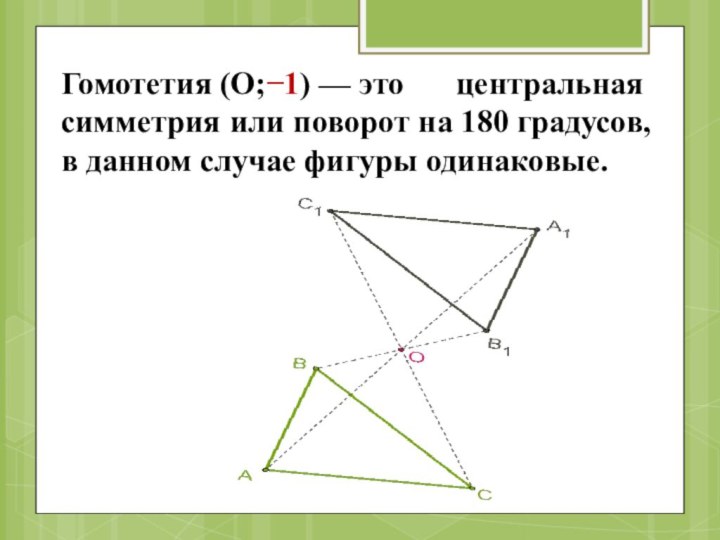
- 21. Гомотетия (О;−1) — это центральная симметрия или поворот на 180 градусов, в данном случае фигуры одинаковые.
- 22. Из определения гомотетии следует, что при k
- 23. Гомотетичные фигуры подобны, но подобные фигуры не всегда гомотетичны (в гомотетии важно расположение фигур).
- 24. Практическое применение гомотетии Гомотетия чаще всего используется
- 25. Для гомотетичных фигур F и F1 в силе формулы отношения периметров и площадей подобных фигур
- 26. Даурен стоит на набережной реки
- 27. Решение задачиПусть на рисунке А
- 28. BМ-длина вытянутой руки Даурена, AB- расстояние между
- 29. Если, например,
- 30. Задание для самостоятельного решения
- 31. Решение
- 32. Выполните задания на сайте www.bilimland.kz
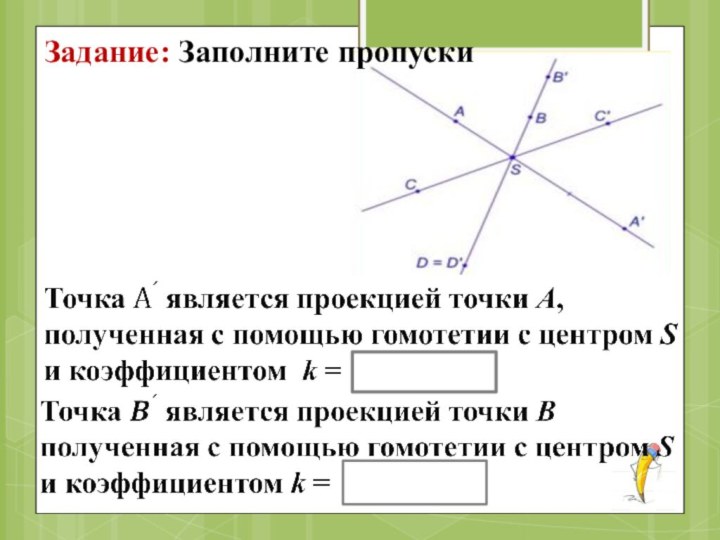
- 33. Задание: Заполните пропуски
- 35. Проверка ответов
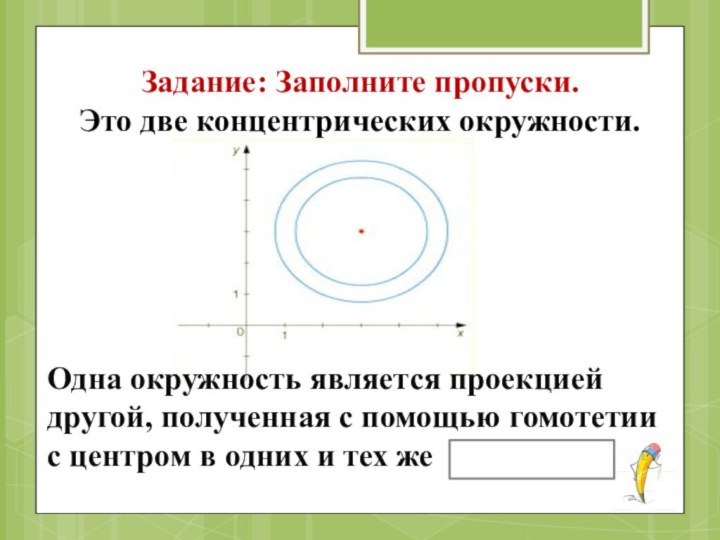
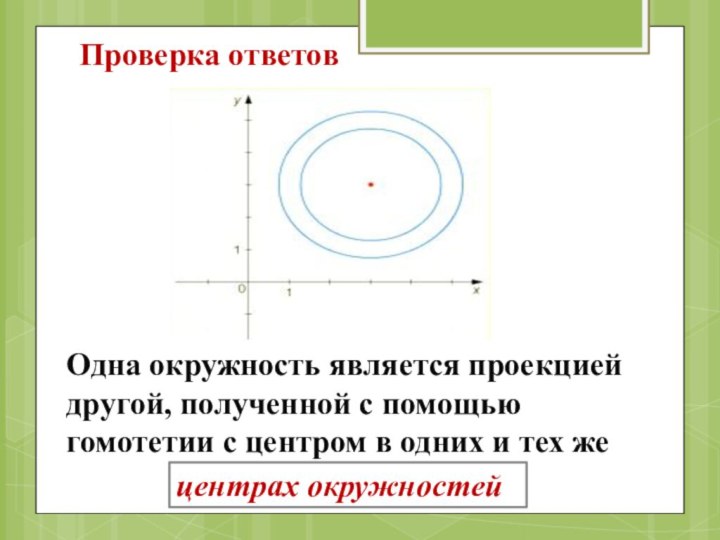
- 37. Задание: Заполните пропуски.Это две концентрических окружности. Одна
- 38. Большая окружность является проекцией окружности, полученной с
- 39. Проверка ответовОдна окружность является проекцией другой, полученной
- 40. Большая окружность является проекцией окружности, полученной с
- 41. Как можно построить фигуру, гомотетичную данной на клетчатом листе?
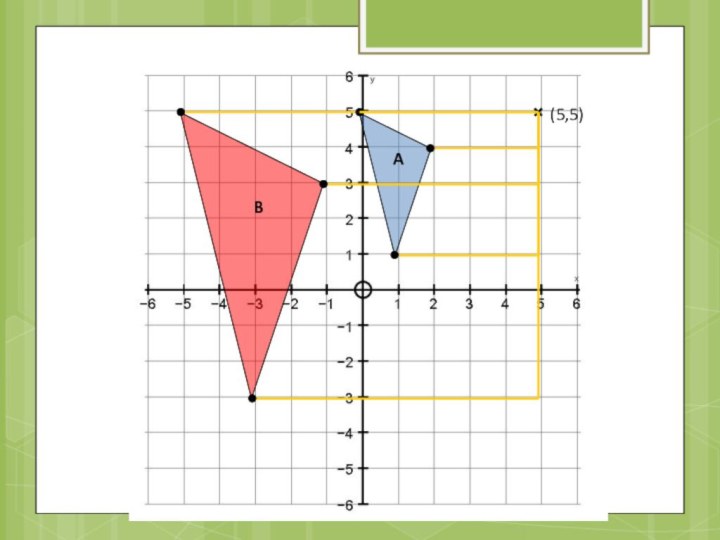
- 43. (5,5)AB
- 44. Enlarge A using the given scale factor
- 45. (iii) Scale factor 4, centre (6,5) to
- 46. Проверь себяABCDE
- 47. ,
- 48. ,
- 49. (-1,1)ABEg enlarge A with scale factor 2
- 50. AEnlarge A using the given scale factor
- 51. (iii) Scale factor -4, centre (2,4) to
- 52. ABCDEПроверь себя
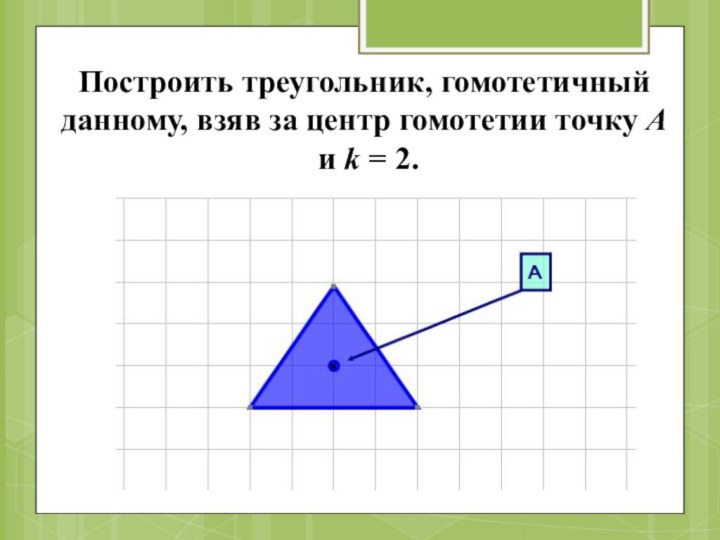
- 53. Построить треугольник, гомотетичный данному, взяв за центр гомотетии точку А и k = 2.
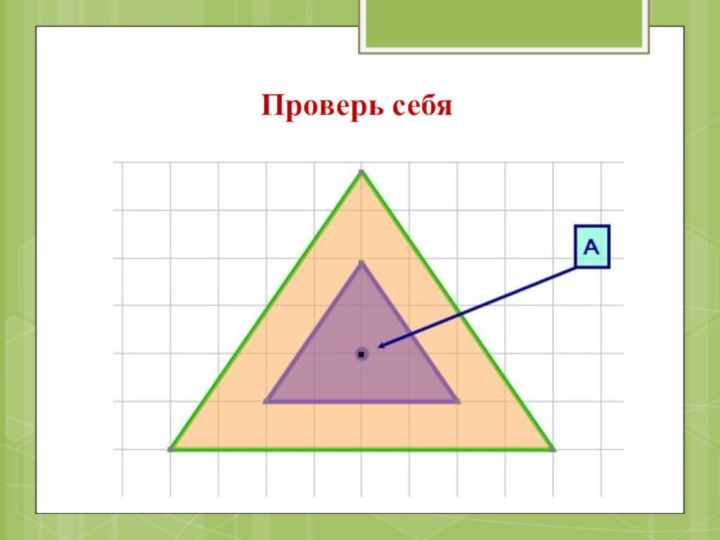
- 54. Проверь себя
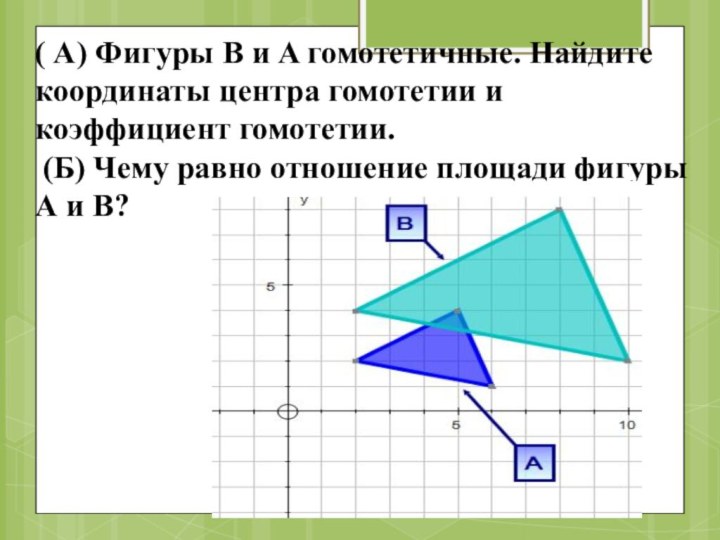
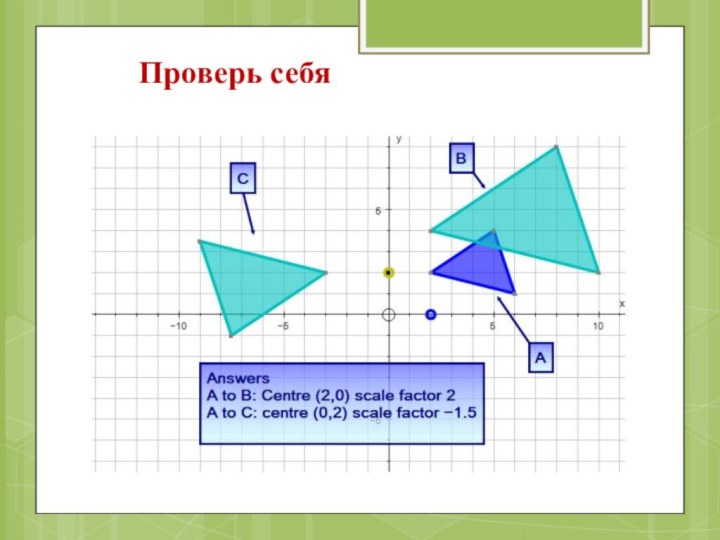
- 55. ( А) Фигуры В и A гомотетичные.
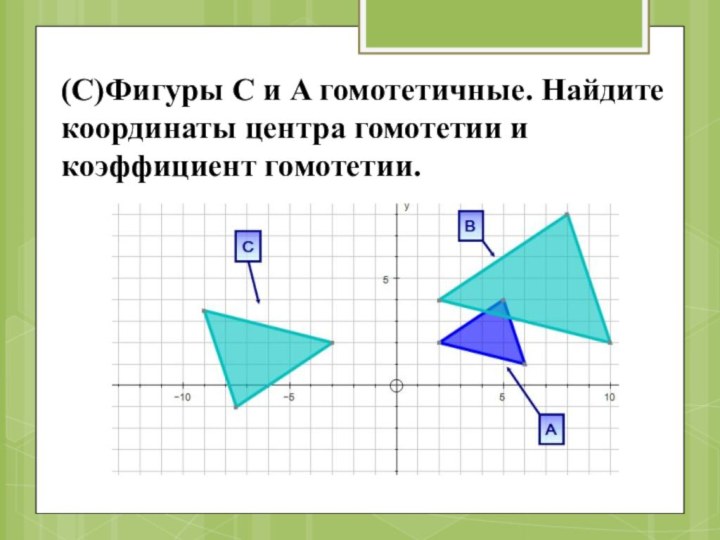
- 56. (С)Фигуры С и A гомотетичные. Найдите координаты центра гомотетии и коэффициент гомотетии.
- 57. Проверь себя
- 58. ВОПРОСЫ НА ЗАСЫПКУ
- 59. Существуют ли прямые, которые переводятся гомотетией сами в себя?
- 60. Ответ: Да, прямые, проходящие через центр гомотетии.
- 61. Даны точки A, B и гомотетичные им
- 62. Ответ: Да. Это точка пересечения прямых AA’ и BB’.
- 63. Как расположены две окружности друг относительно друга, если их центром гомотетии является центр одной из окружностей?
- 64. Ответ: Имеют общий центр
- 65. Как расположены две окружности друг относительно друга,
- 66. Ответ: Касаются внутренним образом.
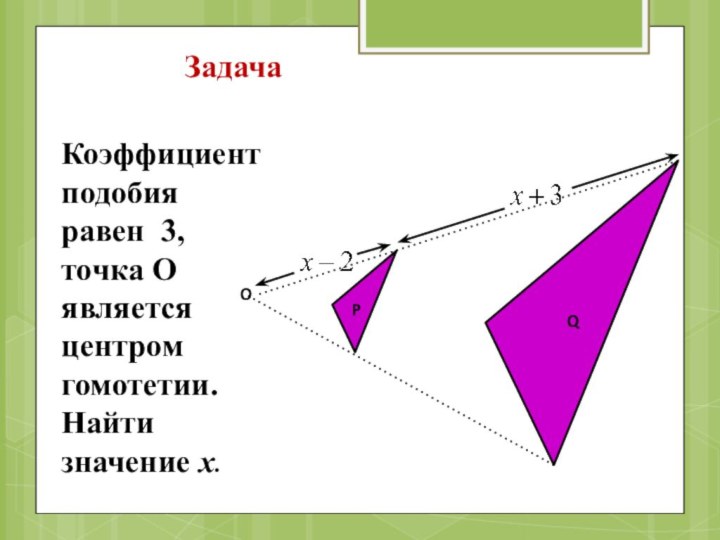
- 67. ЗадачаКоэффициент подобия равен 3, точка О является центром гомотетии. Найти значение х.PQO
- 68. РешениеОтвет: х=7.
- 69. Существуют ли механизмы, инструменты, которые помогают построить фигуру, гомотетичную данной, помимо тех, которые мы уже рассмотрели?
- 70. Пантограф - механизм, который даёт возможность вычертить
- 71. Задача на построение:
- 72. Дано: OMPПостроить: квадрат ABCD, A OM,
- 73. Задача на доказательство:
- 74. Решение:
- 75. Мирас лежит на земле
- 76. Отрезки АВ и СD расположены гомотетично относительно
- 77. Жилой дом.На фотографии виден жилой дом, у
- 78. На данной модели пол у чердака дома-
- 79. Решение. Длина стороны квадрата АВСD равна 12
- 80. Что объединяет эти рисунки?
- 81. ОтветЭти фигуры объединяет гомотетия.
- 82. Видео вопрос
- 83. Поиграем в kahoot.it
- 84. Домашнее задание
- 85. «Если идти по дороге, гомотетичной тайной тропе
- 86. Скачать презентацию
- 87. Похожие презентации
На этом уроке вы узнаете, что такое гомотетия, познакомитесь:с терминами гомотетии;со свойствами гомотетии;научитесь применять свойства гомотетии при решении задач.























































Слайд 4
Задание
Сейчас откроется таблица с терминами по теме «Гомотетия».
Постарайтесь запомнить их за 30 секунд. Через 30 секунд
таблица закроется.Слайд 7 Даурен стоит на набережной реки Сазды.
На противоположном берегу идет Олжас. Даурен отчетливо видит его
перемещение. Может ли он, стоя на одном месте, определить, хотя бы приблизительно, расстояние от себя до Олжаса? Условие: у Даурена нет никаких инструментов.Слайд 8 Гомотетия – одно из важнейших преобразований подобия. Это
преобразование, в котором получаются подобные фигуры (фигуры, у которых
соответствующие углы равны и стороны пропорциональны).
Слайд 9
Подобие фигур
Преобразование плоскости, при котором расстояния
между точками умножаются на одно и то же положительное
число, называется подобием. Само это число называется коэффициентом подобия. Две фигуры F и F' называются подобными, если одна из них переводится в другую подобием.
Слайд 10
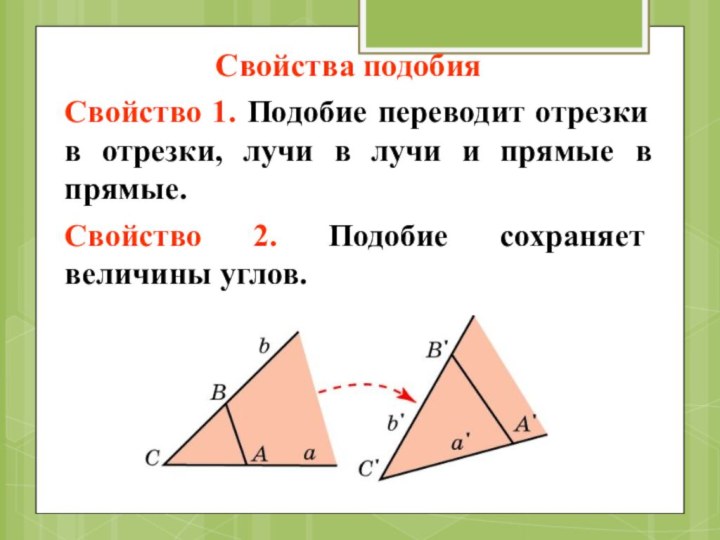
Свойства подобия
Свойство 1. Подобие переводит отрезки в отрезки,
лучи в лучи и прямые в прямые.
Свойство 2. Подобие
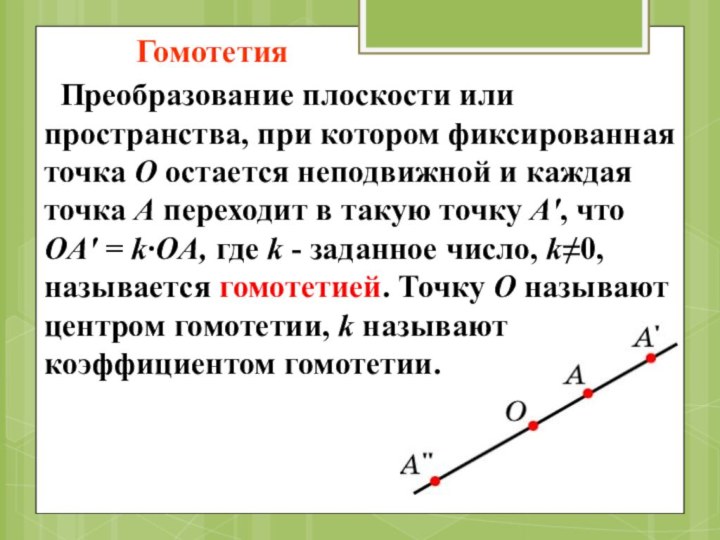
сохраняет величины углов.Слайд 11 Преобразование плоскости или пространства, при котором фиксированная
точка О остается неподвижной и каждая точка А переходит
в такую точку А', чтоOA' = k∙OA, где k - заданное число, k≠0, называется гомотетией. Точку О называют центром гомотетии, k называют коэффициентом гомотетии.
Гомотетия
Слайд 12 В отличие от гомотетии, геометрические преобразования — центральная
симметрия, осевая симметрия, поворот, параллельный перенос являются движениями, т.к.
в них фигура отображается в фигуру, равную данной.Слайд 13 Если фигура F преобразуется в результате гомотетии в
фигуру F1, то фигуры F и F1 называются гомотетичными.
Слайд 14
Свойства гомотетии с коэффициентом k.
Прямая переходит
в параллельную прямую.
Угол переходит в равный ему угол.
Отрезок переходит
в отрезок.Длины всех отрезков изменяются в k раз.
Слайд 15
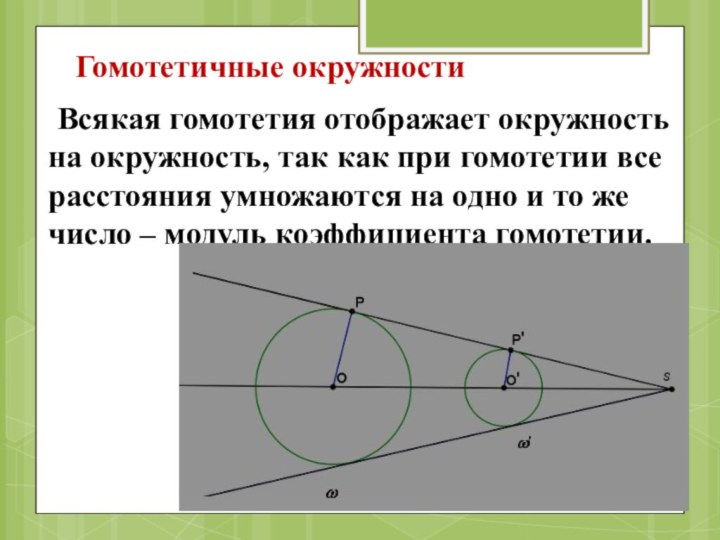
Гомотетичные окружности
Всякая гомотетия отображает окружность на окружность, так
как при гомотетии все расстояния умножаются на одно и
то же число – модуль коэффициента гомотетии.Слайд 16 Чтобы гомотетия была
определена, должен быть задан центр гомотетии и коэффициент.
Это
можно записать так:гомотетия (О;k).
Слайд 17
F
F1
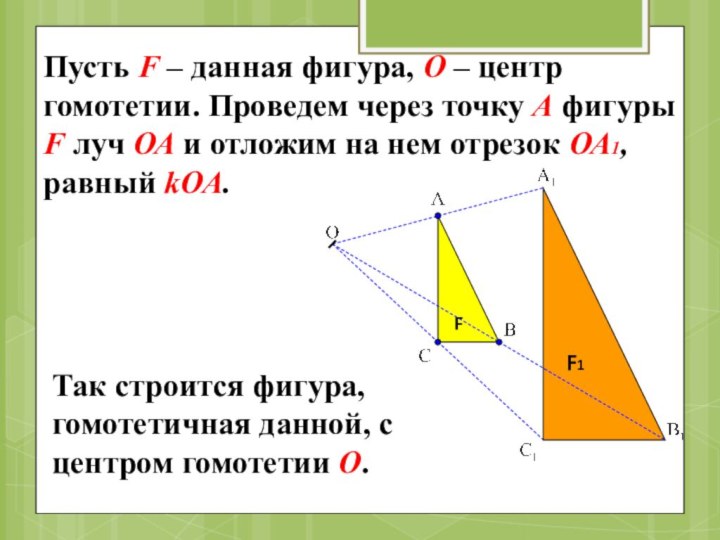
Пусть F – данная фигура, О – центр
гомотетии. Проведем через точку А фигуры F луч ОА
и отложим на нем отрезок ОА1, равный kОА.Так строится фигура, гомотетичная данной, с центром гомотетии О.
Слайд 20 Центр гомотетии может находиться и внутри фигуры. Треугольник A1B1C1
из треугольника ABC получен гомотетией
Слайд 21 Гомотетия (О;−1) — это центральная симметрия или поворот на 180 градусов, в данном
случае фигуры одинаковые.
Слайд 22 Из определения гомотетии следует, что при k =
1 гомотетия является тождественным преобразованием.
При k = –1 гомотетия
становится центральной симметрией.Две гомотетии с центром в O и коэффициентами k и 1/k являются взаимно обратными. Это означает, что если одна из них переводит точку A в точку A1, то другая переводит A1 в A.
Слайд 23 Гомотетичные фигуры подобны, но подобные фигуры не
всегда гомотетичны (в гомотетии важно расположение фигур).
Слайд 24
Практическое применение гомотетии
Гомотетия чаще всего используется в
задачах на нахождение ГМТ
С помощью гомотетии можно строить
подобные фигурыС помощью гомотетии можно находить отношение отрезков, площадей, объемов.
Слайд 25 Для гомотетичных фигур F и F1 в силе
формулы
отношения периметров
и площадей подобных фигур
Слайд 26 Даурен стоит на набережной реки Сазды.
На противоположном берегу идет Олжас. Даурен отчетливо видит его
перемещение. Может ли он, стоя на одном месте, определить, хотя бы приблизительно, расстояние от себя до Олжаса? Условие: у Даурена нет никаких инструментов.
Слайд 27
Решение задачи
Пусть на рисунке А и
В – глаза Даурена, точка М - конец пальца
его вытянутой руки, точка C– первое положение Олжаса, D - второе.Слайд 28 BМ-длина вытянутой руки Даурена, AB- расстояние между зрачками
его глаз, CD измерено шагами Олжаса (шаг можно принять
в среднем равным 3/4 м). Следовательно, неизвестное расстояние от Даурена до Олжаса на противоположном берегу рекиЗначит,
Слайд 29 Если, например, расстояние
между зрачками глаз у Даурена 6 см, длина от
конца вытянутой руки до глаз 60 см, а Олжас сделал от А до В, скажем 14 шагов, то расстояние между ними
Слайд 37
Задание: Заполните пропуски.
Это две концентрических окружности.
Одна окружность
является проекцией другой, полученная с помощью гомотетии с центром
в одних и тех жеСлайд 38 Большая окружность является проекцией окружности, полученной с помощью
гомотетии с коэффициентом равным отношению радиуса
окружности к радиусу
окружности
Слайд 39
Проверка ответов
Одна окружность является проекцией другой, полученной с
помощью гомотетии с центром в одних и тех же
центрах
окружностейСлайд 40 Большая окружность является проекцией окружности, полученной с помощью
гомотетии с коэффициентом равным отношению радиуса
окружности к радиусу
окружностибольшей
меньшей
Слайд 44
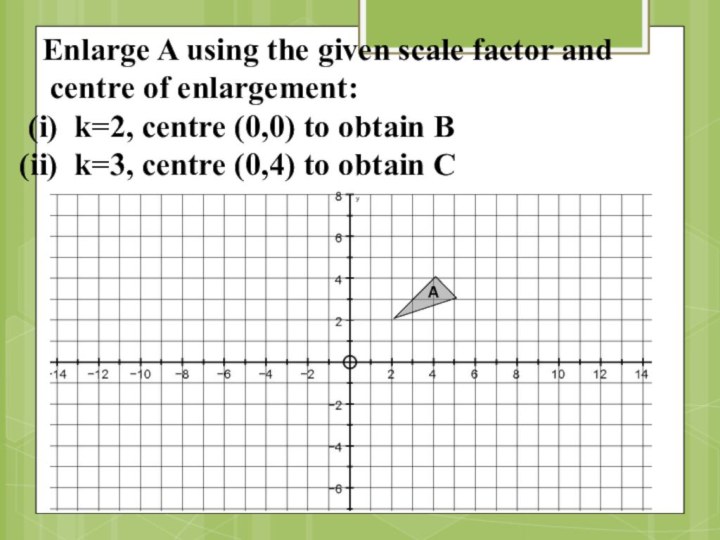
Enlarge A using the given scale factor and
centre of enlargement:
k=2, centre (0,0) to obtain B
k=3, centre
(0,4) to obtain CA
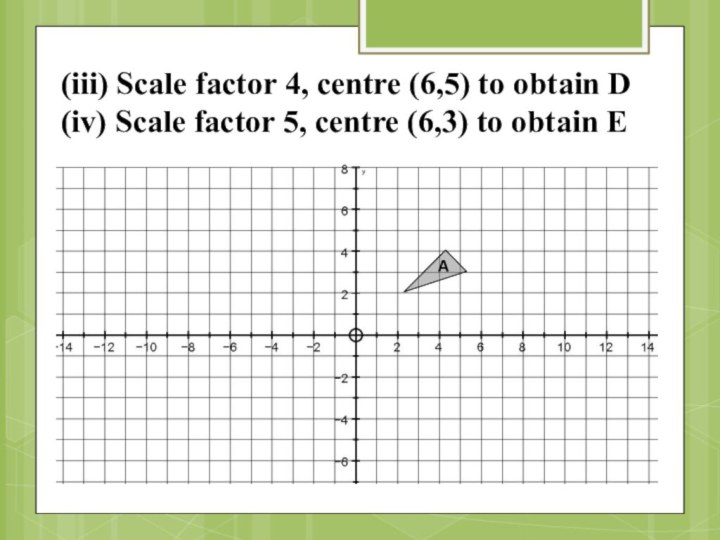
Слайд 45 (iii) Scale factor 4, centre (6,5) to obtain
D (iv) Scale factor 5, centre (6,3) to obtain
EA
Слайд 47
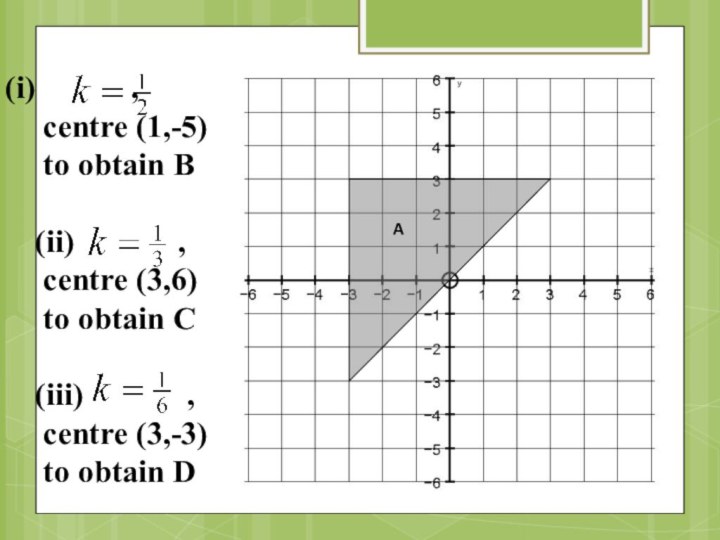
,
centre (1,-5)
to obtain B
(ii)
, centre (3,6)
to obtain C
(iii) ,
centre (3,-3)
to obtain D
A
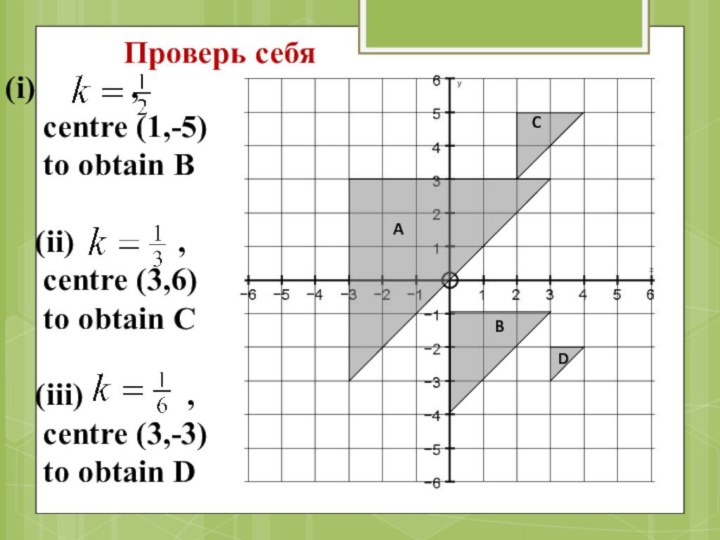
Слайд 48
,
centre (1,-5)
to obtain B
(ii)
, centre (3,6)
to obtain C
(iii) ,
centre (3,-3)
to obtain D
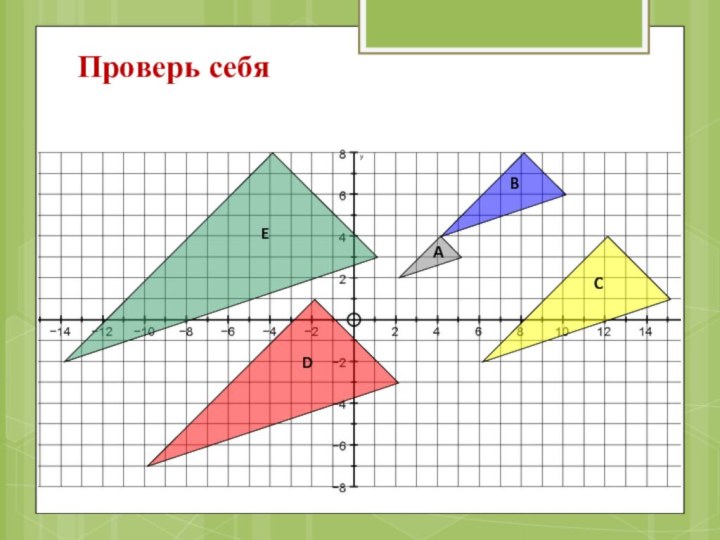
A
B
C
D
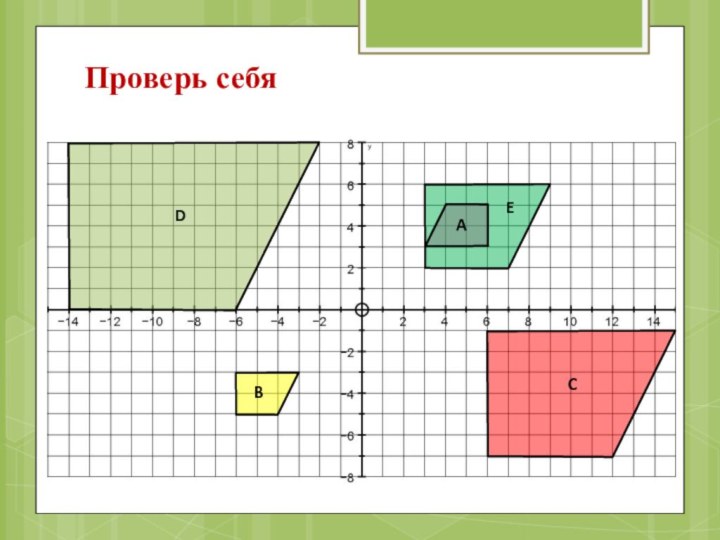
Проверь себя
Слайд 49
(-1,1)
A
B
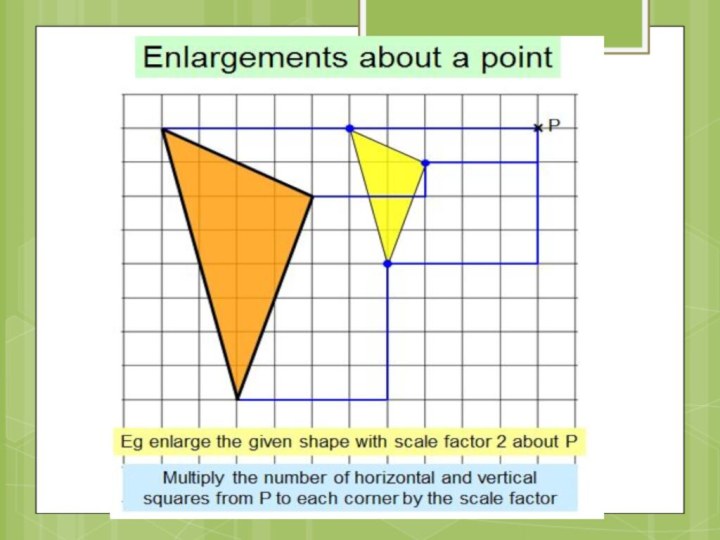
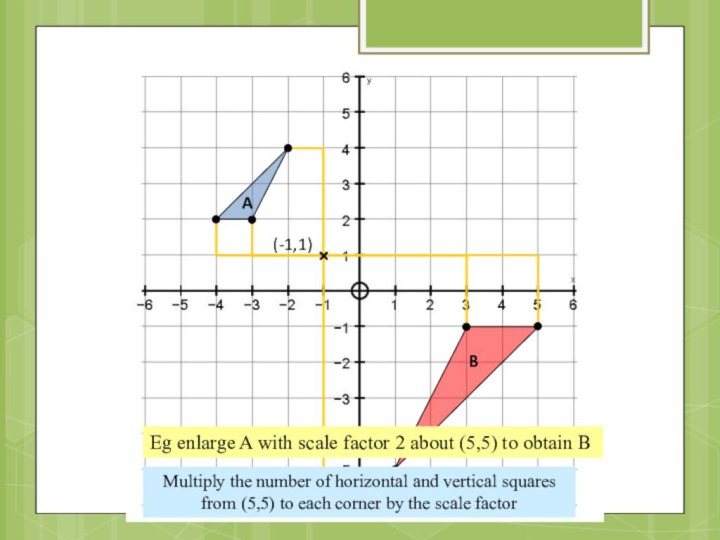
Eg enlarge A with scale factor 2 about
(5,5) to obtain B
Multiply the number of horizontal and
vertical squares from (5,5) to each corner by the scale factor
Слайд 50
A
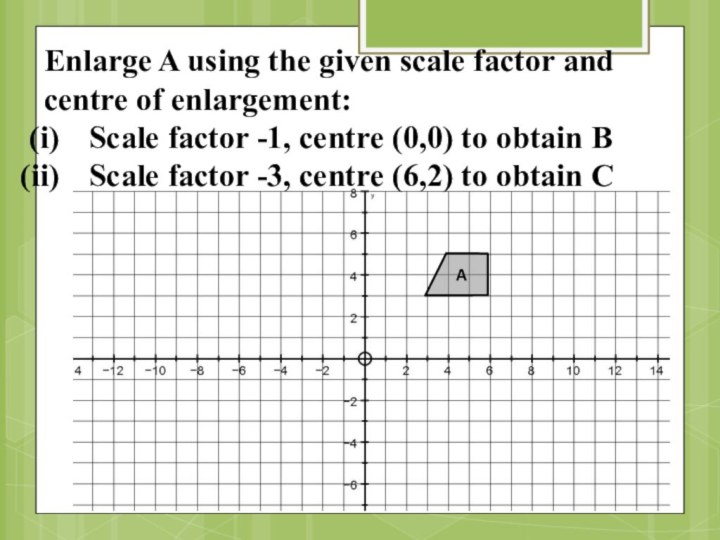
Enlarge A using the given scale factor and
centre
of enlargement:
Scale factor -1, centre (0,0) to obtain B
Scale factor -3, centre (6,2) to obtain C
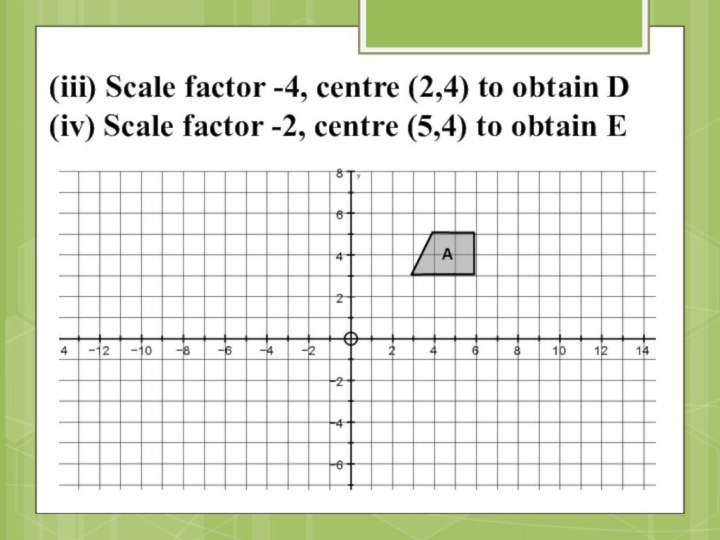
Слайд 51 (iii) Scale factor -4, centre (2,4) to obtain
D (iv) Scale factor -2, centre (5,4) to
obtain EA
Слайд 55 ( А) Фигуры В и A гомотетичные. Найдите
координаты центра гомотетии и коэффициент гомотетии. (Б) Чему
равно отношение площади фигуры А и В?Слайд 61 Даны точки A, B и гомотетичные им точки
A´, B´ соответственно. Можно ли найти центр данной гомотетии?
Слайд 63 Как расположены две окружности друг относительно друга, если
их центром гомотетии является центр одной из окружностей?
Слайд 65 Как расположены две окружности друг относительно друга, если
их центром гомотетии является точка, принадлежащая одной из данных
окружностей?
Слайд 67
Задача
Коэффициент подобия равен 3, точка О является центром
гомотетии. Найти значение х.
P
Q
O
Слайд 69 Существуют ли механизмы, инструменты, которые помогают построить фигуру,
гомотетичную данной, помимо тех, которые мы уже рассмотрели?
Слайд 70 Пантограф - механизм, который даёт возможность вычертить фигуру,
перспективно-подобную любой заданной фигуре, притом с любым положительным коэффициентом
подобия. Впервые он был создан вначале XVII века.Слайд 71 Задача на построение:
Впишите в данный треугольник квадрат, у
которого две вершины лежат на одной стороне, а две другие вершины — на двух других сторонах.
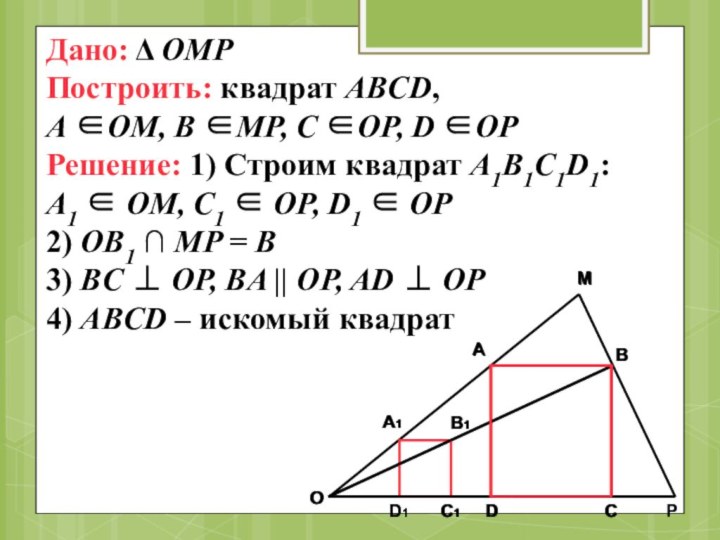
Слайд 72
Дано: OMP
Построить: квадрат ABCD,
A OM, B
MP, C OP, D OP
Решение: 1) Строим квадрат A1B1C1D1:
A1 OM, C1 OP, D1 OP
2) OB1 ∩ MP = B
3) BC OP, BA || OP, AD OP
4) ABCD – искомый квадрат
O
D1
C1
D
C
B
M
A
A1
B1
O
D1
C1
D
C
P
B
M
A
A1
B1
Слайд 75 Мирас лежит на земле 45
футов от своей палатки. Верхняя часть палатки и вершина
высокой скалы находятся в его прямой видимости . Высота его палатки 10 футов. Какой высоты этот обрыв, если расстояние между обрывом и его палаткой 400 футов?Прикладная задача
Слайд 76 Отрезки АВ и СD расположены гомотетично относительно точки
О, следовательно:
Отсюда получаем:
Значит,
Ответ: Длина обрыва 2002,5 футов
Решение:
Слайд 77
Жилой дом.
На фотографии виден жилой дом, у которого
крыша имеет форму пирамиды. Ниже изображена сделанная учащимся математическая
модель крыши дома и указаны длины некоторых отрезков.Слайд 78 На данной модели пол у чердака дома- квадрат
АВСD. Балки, на которые опирается крыша, является сторонами блока,
имеющего форму, прямоугольного параллелепипеда EFGHKLMN, E - середина ребра AT, F- середина ВТ, G- середина СТ, Н – середина DT. Все ребра пирамиды 12 м.Задание:
а) Вычислите площадь пола чердака АВСD.
b) Найдите длину отрезка EF – горизантальной стороны бетонного блока.
Слайд 79 Решение. Длина стороны квадрата АВСD равна 12 м.
Значит, площадь квадрата равна
Ответ: 144 кв.м
Поскольку Е -
середина ребра АТ, а F – середина ВТ, значит ЕF – средняя линия треугольника АВТ. Поэтому ЕF в 2 раза меньше длины отрезка. АВ=12:2=6 м.
Ответ: 6 м
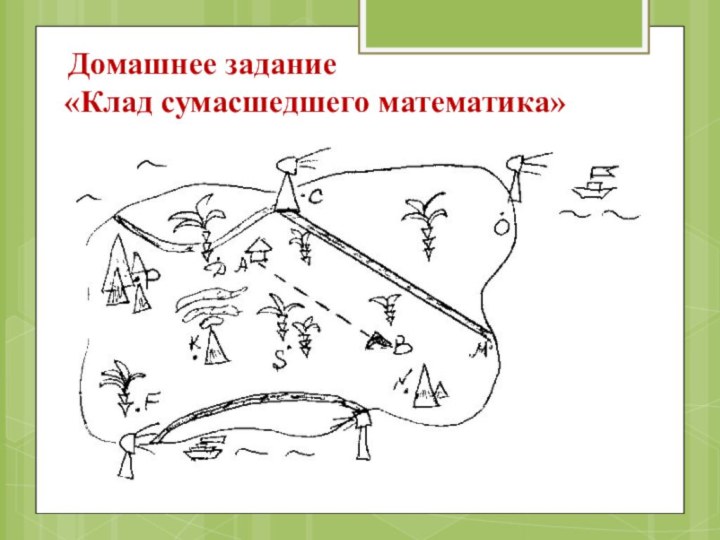
Слайд 85 «Если идти по дороге, гомотетичной тайной тропе относительно
вулкана и дойти до маяка, а затем перейти в
точку симметричную маяку относительно большой пальмы, то рядом, у подножия большой подобной горы зарыт клад».Зная, что тайная тропа обозначена отрезком АВ, найти в какой точке зарыт клад.