- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Гл. 4 Урок 2. Касательная к окружности
Содержание
- 2. Касательная к окружностиУчебная презентация
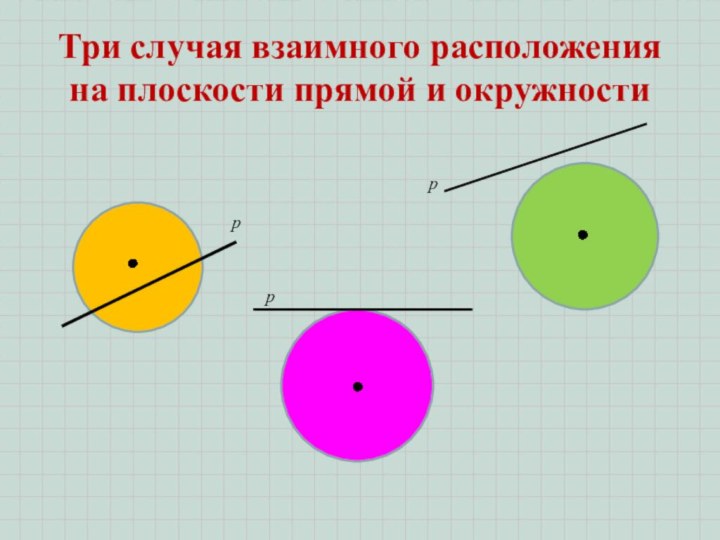
- 3. Три случая взаимного расположения на плоскости прямой и окружностиррр
- 4. Сколько общих точек могут иметь прямая и
- 5. ОАПрямая, имеющая с окружностью только одну общую
- 6. Касательная к окружности перпендикулярна к радиусу, проведённому
- 7. ОДоказательство: r = ОА; r = dтолько
- 8. Дано: окружность, АВ и АС – касательные;
- 9. Задача на построение касательной к окружностиДано:
- 10. Решение задач
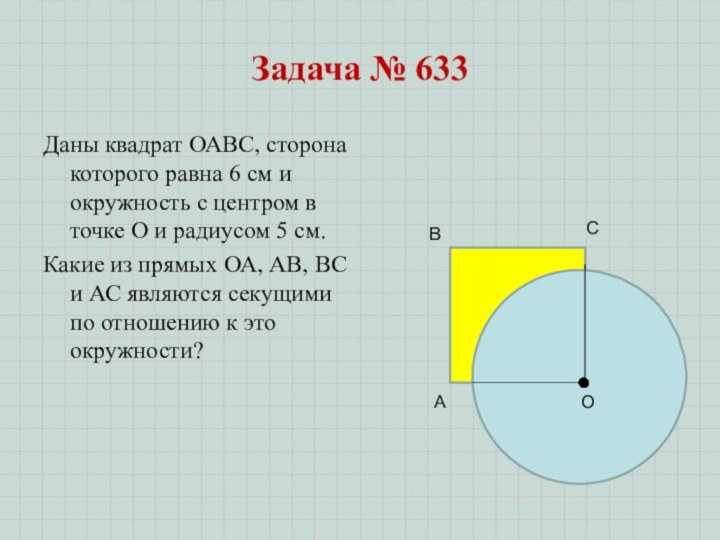
- 11. Задача № 638Прямая АВ касается окружности с
- 12. Задача № 640Даны окружность с центром О
- 13. Задача № 635Прямая АВ касается окружности с
- 14. Задача № 637Угол между диаметром АВ и
- 15. Скачать презентацию
- 16. Похожие презентации






Слайд 4
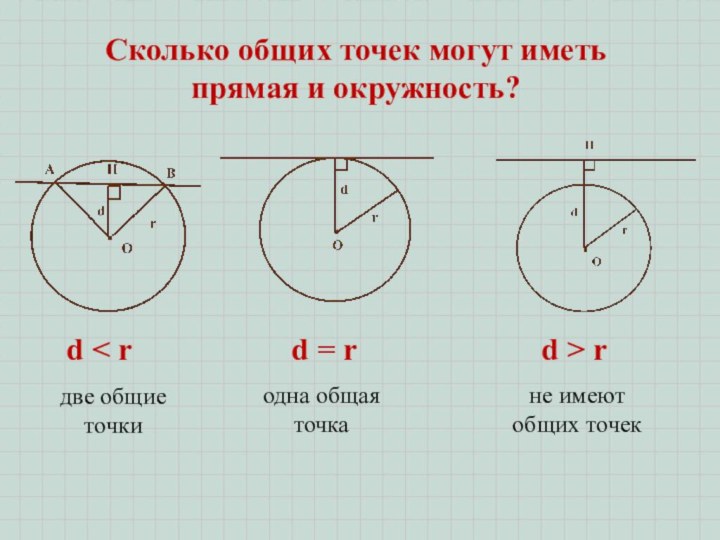
Сколько общих точек могут иметь
прямая и окружность?
d
< r
d = r
d > r
две общие точки
одна общая
точкане имеют общих точек
Слайд 5
О
А
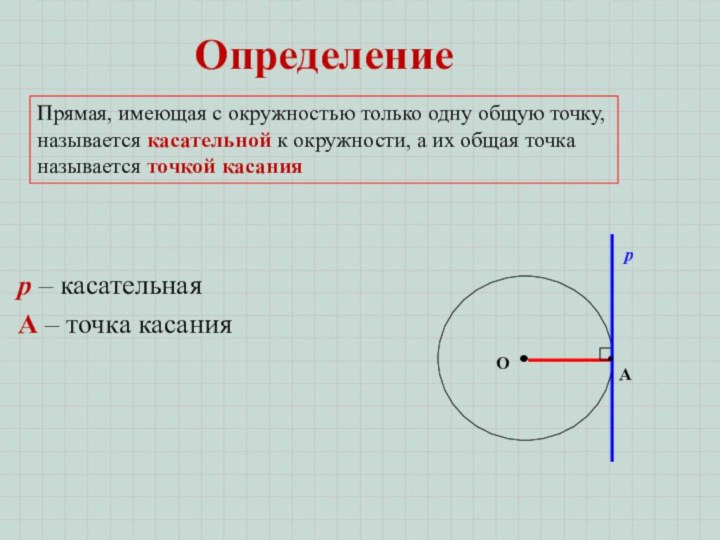
Прямая, имеющая с окружностью только одну общую точку,
называется касательной к окружности, а их общая точка называется
точкой касанияр
p – касательная
А – точка касания
Определение
Слайд 6 Касательная к окружности перпендикулярна к радиусу, проведённому в
точку касания.
Дано: р – касательная;
Окружность (О; r);
А –
точка касания.Доказать: р ОА.
Доказательство:
Предположим, что это не так. То есть ОА будет наклонной. Но любая наклонная, проведенная из той же точки, что и перпендикуляр, будет больше перпендикуляра. ОН < ОА, то ОН < r. => d < r Значит, прямая р и окружность имеют две общие точки, что неверно => р ОА.
Теорема
(свойство касательной)
Слайд 7
О
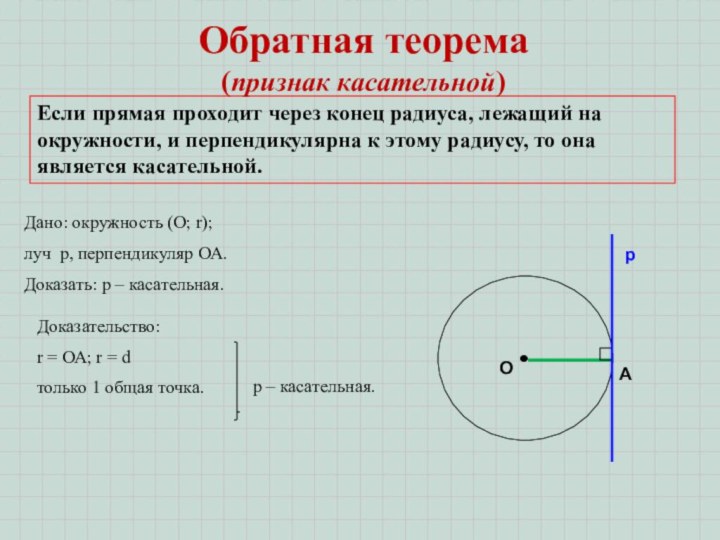
Доказательство:
r = ОА; r = d
только 1
общая точка.
p – касательная.
А
Дано: окружность (О; r);
луч р,
перпендикуляр ОА.Доказать: р – касательная.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Обратная теорема
(признак касательной)
р
Слайд 8
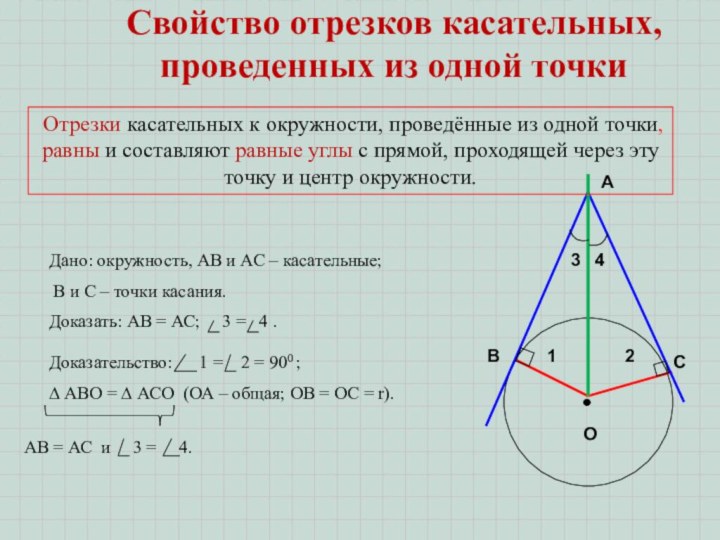
Дано: окружность, АВ и АС – касательные;
В
и С – точки касания.
Доказать: АВ = АС;
3 = 4 .Доказательство: 1 = 2 = 900 ;
∆ АВО = ∆ АСО (ОА – общая; ОВ = ОС = r).
АВ = АС и 3 = 4.
О
А
B
С
2
4
3
1
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойство отрезков касательных, проведенных из одной точки
Слайд 9
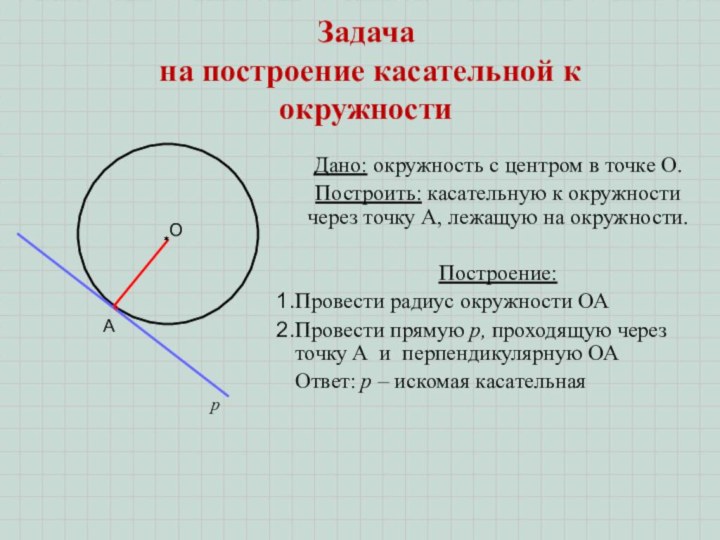
Задача
на построение касательной к окружности
Дано: окружность с
центром в точке О.
Построить: касательную к окружности через
точку А, лежащую на окружности.Построение:
Провести радиус окружности ОА
Провести прямую р, проходящую через точку А и перпендикулярную ОА
Ответ: р – искомая касательная
О
А
p
Слайд 11
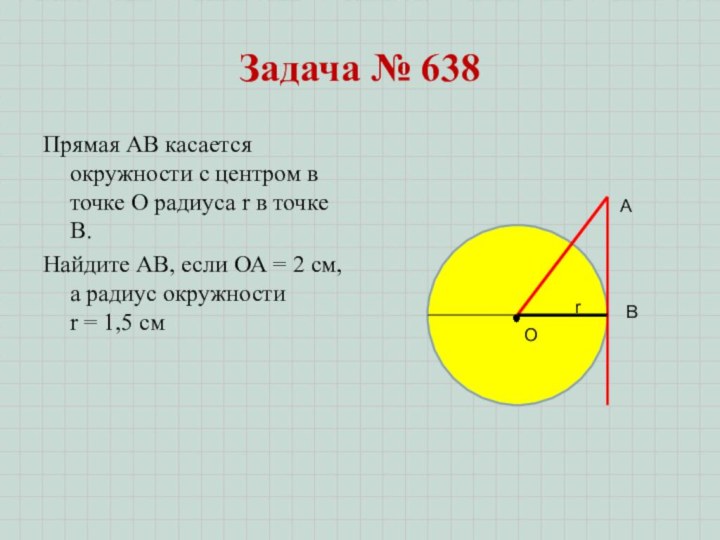
Задача № 638
Прямая АВ касается окружности с центром
в точке О радиуса r в точке В.
Найдите АВ,
если ОА = 2 см, а радиус окружности r = 1,5 смВ
О
А
r
Слайд 12
Задача № 640
Даны окружность с центром О и
радиусом 4,5 см и точка А. Через точку
А проведены две касательные к окружности.Найдите угол между ними, если ОА= 9 см.
В
О
А
r
C
Слайд 13
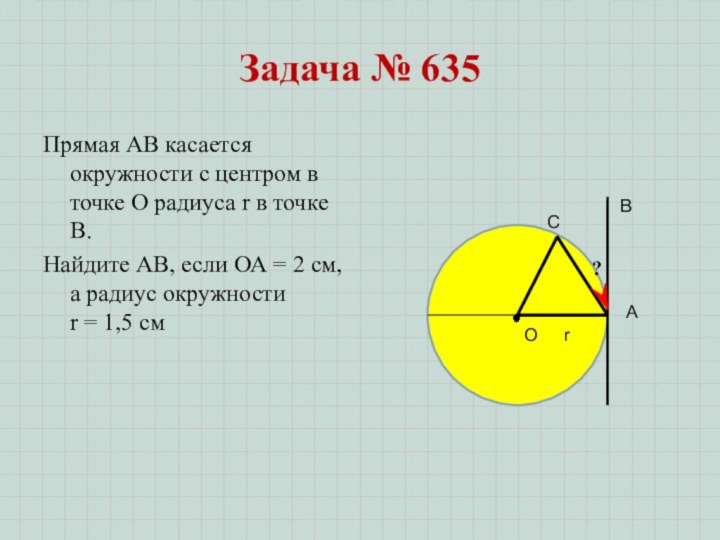
Задача № 635
Прямая АВ касается окружности с центром
в точке О радиуса r в точке В.
Найдите АВ,
если ОА = 2 см, а радиус окружности r = 1,5 смА
О
В
r
С
?
Слайд 14
Задача № 637
Угол между диаметром АВ и хордой
АС равен 30°. Через точку С проведена касательная, пересекающая
прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.В
О
А
С
D
Доказательство:
∆ АОС = равнобедренный, его боковые стороны равны радиусу окружности, тогда < АСО = 30°.
< СОD – внешний по отношению к ∆ АОС, значит он равен сумме двух внутренних углов этого треугольника, не смежного с ним, т.е. < СОD = 30° + 30°= 60°
< ОСD – прямой, тогда < СDО = 30°. Получаем,
в ∆ АСD два равных угла (< СAD = < CDA = 30°). Значит он – равнобедренный, Ч. Т. Д.