- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему и конспект урока по геометрии на тему Движение (8 класс)
Содержание
- 2. Цели урокаРассмотреть различные преобразования фигур.Изучить понятие движение.Осуществить самоконтроль посредством тестирования.
- 3. Осевая симметрия
- 4. Центральная симметрия
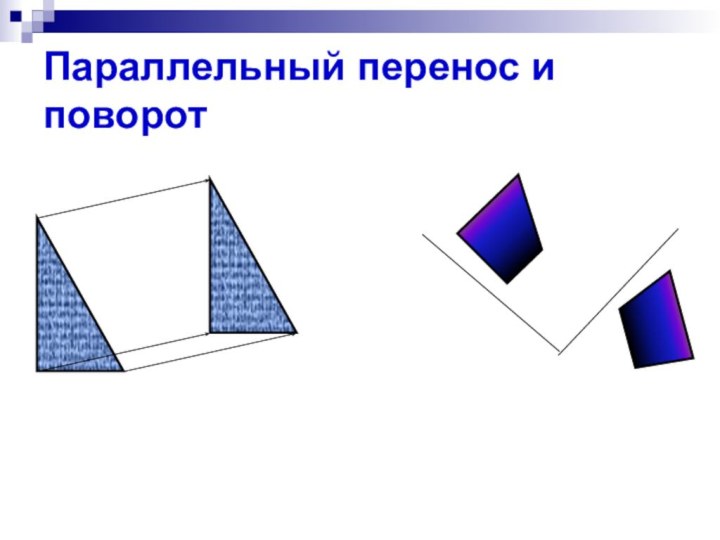
- 6. Параллельный перенос и поворот
- 7. ОпределениеДвижение – это отображение плоскости на себя, сохраняющее расстояния
- 8. Виды движенияОсевая симметрияЦентральная симметрияПоворотПараллельный перенос
- 9. Параллельным переносом на вектор а называется отображение
- 10. Фигура называется центрально-симметричной, если преобразование симметрии относительно
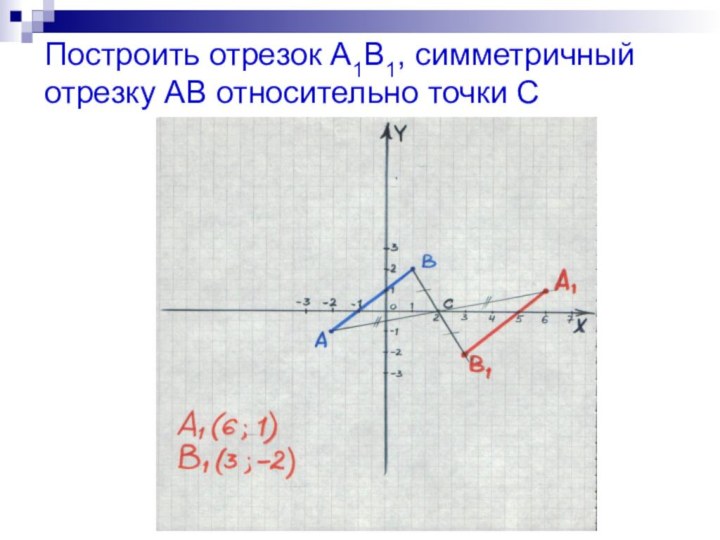
- 12. Построить отрезок А1В1, симметричный отрезку АВ относительно точки C
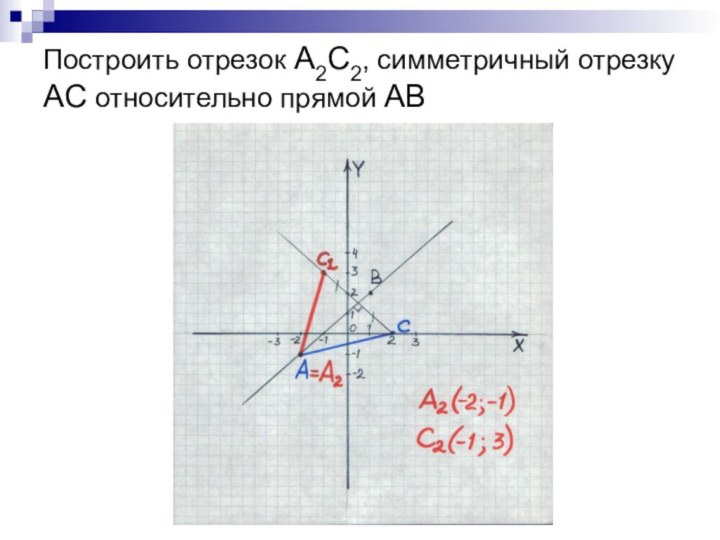
- 13. Построить отрезок А2C2, симметричный отрезку АC относительно прямой АB
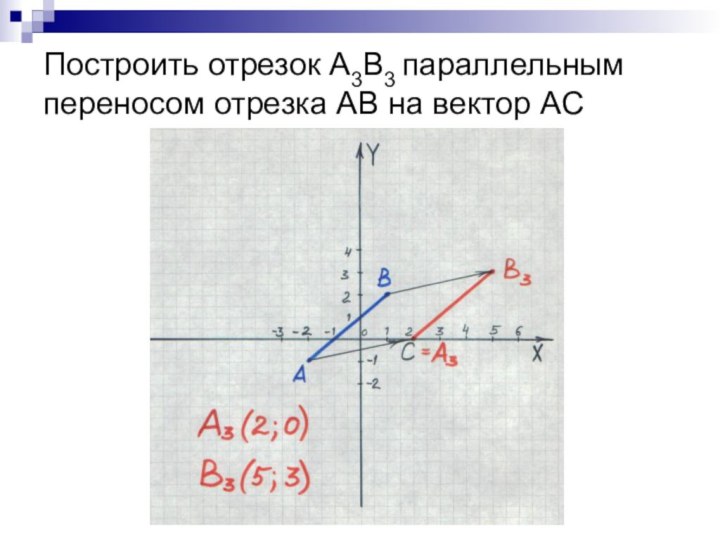
- 14. Построить отрезок А3B3 параллельным переносом отрезка АB на вектор АC
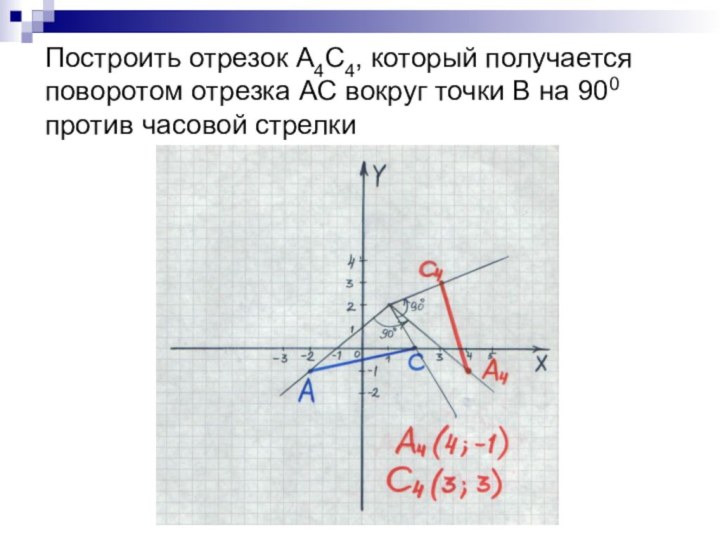
- 15. Построить отрезок А4C4, который получается поворотом отрезка АC вокруг точки B на 900 против часовой стрелки
- 20. Может ли у треугольника быть центр симметрии?Сколько
- 21. Шутка об осевой симметрии Однажды
- 22. Скачать презентацию
- 23. Похожие презентации
Цели урокаРассмотреть различные преобразования фигур.Изучить понятие движение.Осуществить самоконтроль посредством тестирования.














Слайд 2
Цели урока
Рассмотреть различные преобразования фигур.
Изучить понятие движение.
Осуществить самоконтроль
посредством тестирования.
Слайд 9
Параллельным переносом на вектор а называется отображение плоскости
на себя, при котором каждая точка М отображается в
такую точку М1, что вектор ММ1 равен вектору а.Поворотом вокруг точки О на угол А называется отображение плоскости на себя, при котором каждая точка М отображается в такую мочку М1, что ОМ=ОМ1 и угол МОМ1 равен углу А.
Слайд 10
Фигура называется центрально-симметричной, если преобразование симметрии относительно точки
О переводит фигуру в себя.
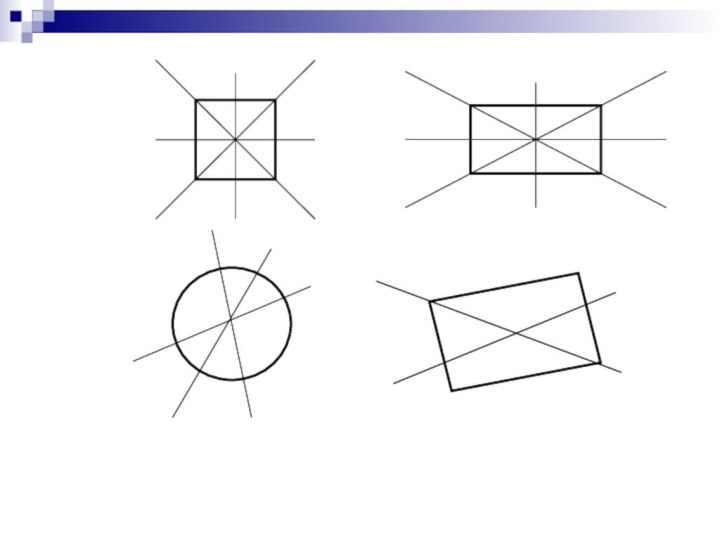
Фигура называется симметричной относительно прямой,
если преобразование симметрии относительно прямой переводит фигуру в себя.Слайд 15 Построить отрезок А4C4, который получается поворотом отрезка АC
вокруг точки B на 900 против часовой стрелки
Слайд 20
Может ли у треугольника быть центр симметрии?
Сколько осей
симметрии у равностороннего треугольника?
Является ли центральная симметрия частным случаем
поворота?Является ли поворот центральной симметрией?
Слайд 21
Шутка об осевой симметрии
Однажды чужеземец,
восхищенный красотой знаменитого бухарского минарета Калан, воскликнул:
- Как вы
строите такие высокие минареты?- Очень просто, - ответил Ходжа Насреддин и, не преминув блеснуть своим обычным остроумием, пояснил, - сначала выкапываем глубокий колодец, а потом выворачиваем его наизнанку.