- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Найти площадь криволинейной трапеции
Содержание
- 2. Определение производной:Найти производную функции по определению:© Комаров Р.А.
- 3. Вставьте вместо *Определение первообразной:© Комаров Р.А.
- 4. Будут ли первообразными следующие функциидля функции © Комаров Р.А.
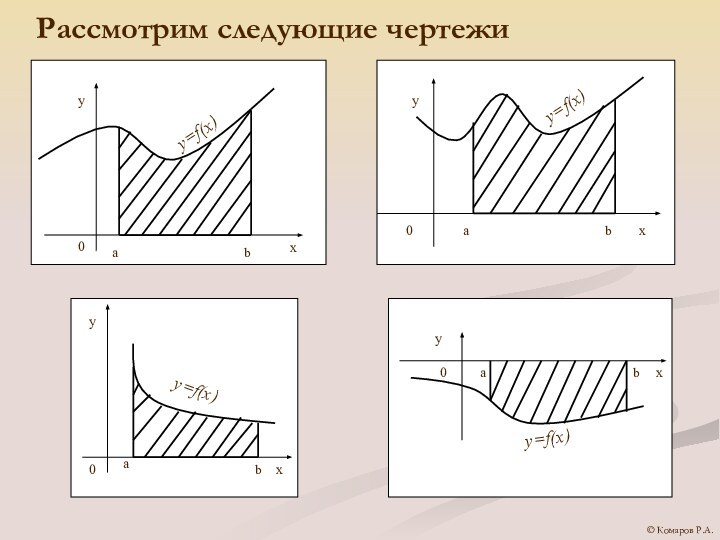
- 5. Рассмотрим следующие чертежи© Комаров Р.А.
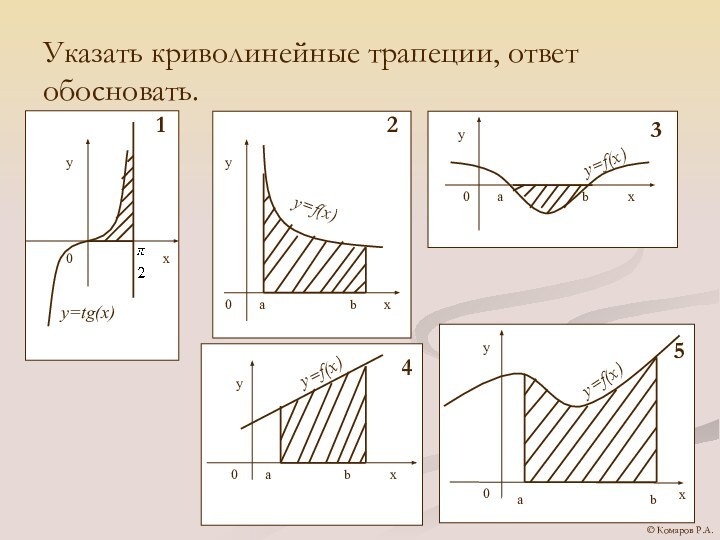
- 6. Определение: фигура, ограниченная графиком непрерывной и не
- 7. Указать криволинейные трапеции, ответ обосновать.© Комаров Р.А.
- 8. Как вычислить площадь данной криволинейной трапеции?Площадь равна произведениюполусуммы основанийтрапеции на высоту. ?© Комаров Р.А.
- 9. Площадь криволинейной трапеции© Комаров Р.А.
- 10. Вычислите площадь криволинейной трапеции 2-мя способами1) Используя
- 11. Теорема: Если f – непрерывная и неотрицательная
- 12. Доказательство: Выберем между a и b на
- 13. Докажем , что– это площадь криволинейной трапеции,
- 14. Возьмем прямоугольник, равновеликий этой криволинейной трапеции и
- 15. Найдем С:ТогдаТаким образом, мы доказали теорему и
- 16. Вычислить площадь фигуры, ограниченной линиямиРешение:Ответ: © Комаров Р.А.
- 17. Скачать презентацию
- 18. Похожие презентации
Определение производной:Найти производную функции по определению:© Комаров Р.А.
![Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция,](/img/tmb/12/1123800/2d31c5576eb56d6820cba8d352d01b1c-720x.jpg "Найти площадь криволинейной трапеции")
![Докажем , что– это площадь криволинейной трапеции, опирающейся на отрезок[x; x+∆x] (площадь](/img/tmb/12/1123800/aefd304f6360276189d7521e8df0bf6a-720x.jpg "Найти площадь криволинейной трапеции")
Слайд 6 Определение: фигура, ограниченная графиком непрерывной и не меняющей
своего знака на отрезке [a; b] функции, прямыми x=a,
x=b и отрезком [a; b] называется криволинейной трапецией.© Комаров Р.А.
Слайд 8
Как вычислить площадь данной криволинейной трапеции?
Площадь равна произведению
полусуммы
оснований
трапеции на высоту.
?
© Комаров Р.А.
Слайд 10
Вычислите площадь криволинейной трапеции 2-мя способами
1) Используя формулу
площади
трапеции из геометрии, получим:
2) Найдите F(x) и вычислите
S
по формуле S=F(b)-F(a) © Комаров Р.А.
Слайд 11 Теорема: Если f – непрерывная и неотрицательная на отрезке
[a; b] функция, а F – ее первообразная на
этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b], т.е. S=F(b)-F(a).Дано: f – функция непрерывная, неотрицательная на отрезке [a; b]
криволинейная трапеция
Док-ть: S=F(b)-F(a)
© Комаров Р.А.
Слайд 12
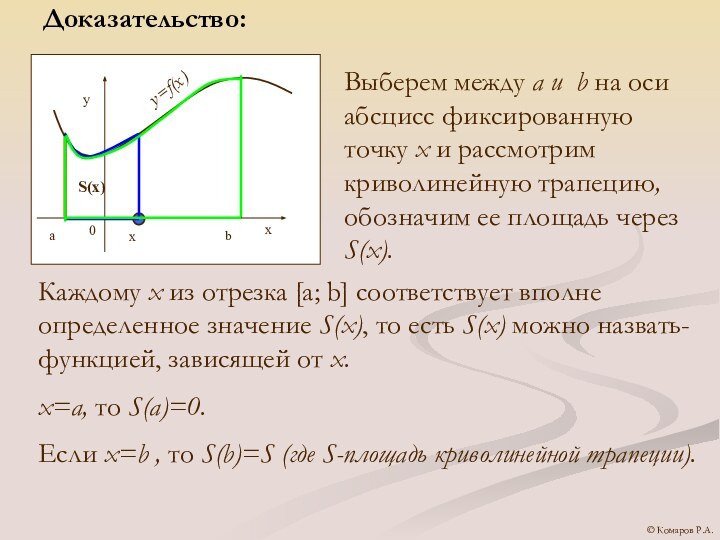
Доказательство:
Выберем между a и b на оси абсцисс
фиксированную точку х и рассмотрим криволинейную трапецию, обозначим ее
площадь через S(x).Каждому х из отрезка [a; b] соответствует вполне определенное значение S(x), то есть S(x) можно назвать- функцией, зависящей от х.
х=а, то S(a)=0.
Если х=b , то S(b)=S (где S-площадь криволинейной трапеции).
© Комаров Р.А.
Слайд 13
Докажем , что
– это площадь криволинейной трапеции, опирающейся
на отрезок[x; x+∆x] (площадь фигуры заштрихованной на рисунке)
© Комаров
Р.А.
Слайд 14
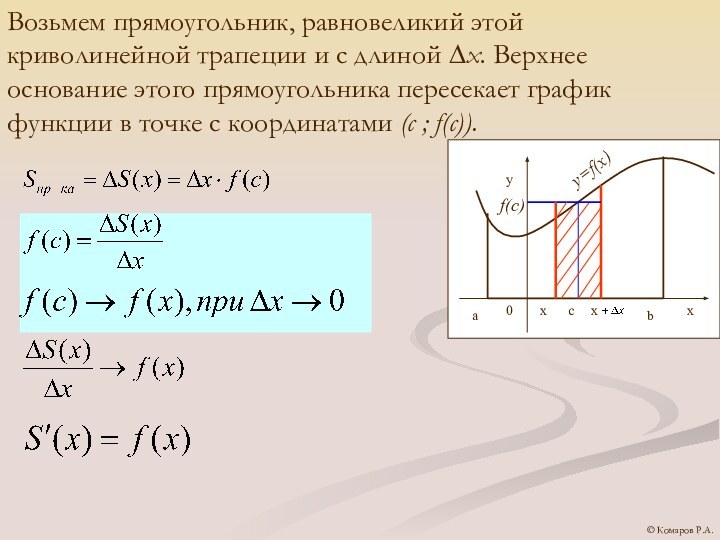
Возьмем прямоугольник, равновеликий этой криволинейной трапеции и с
длиной ∆х. Верхнее основание этого прямоугольника пересекает график функции
в точке с координатами (с ; f(c)).© Комаров Р.А.
Слайд 15
Найдем С:
Тогда
Таким образом, мы доказали теорему и в
