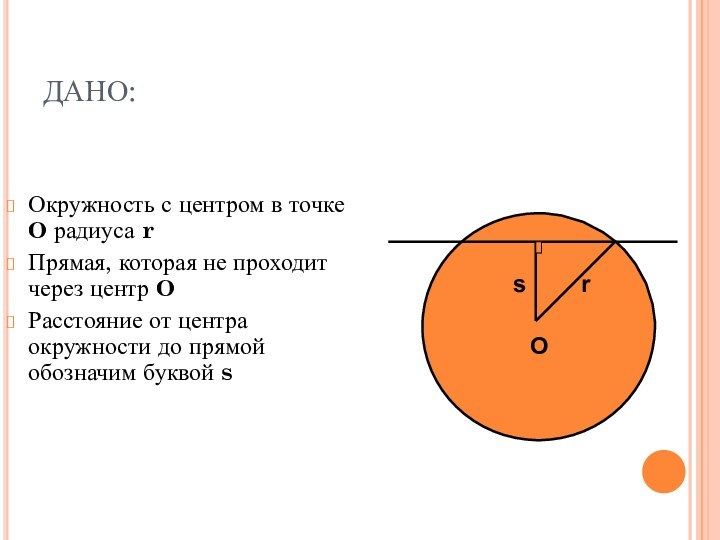
которая не проходит через центр О
Расстояние от центра окружности
до прямой обозначим буквой sO
r
s
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





O
r
s
O
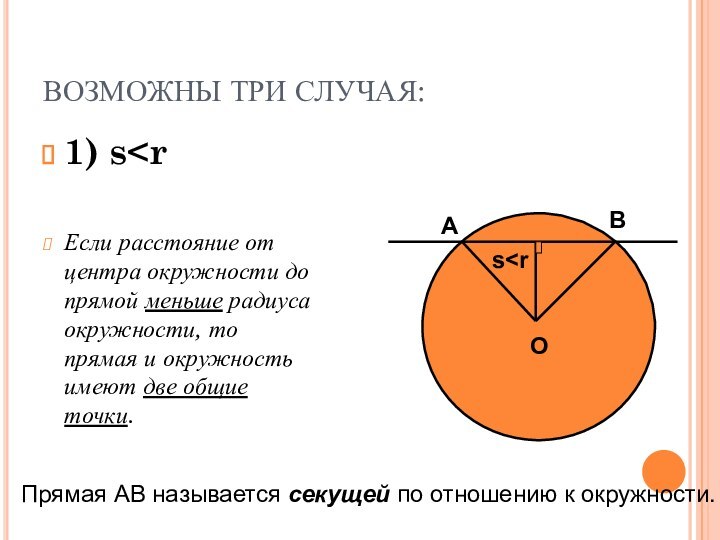
s А В Прямая АВ называется секущей по отношению к окружности.
O
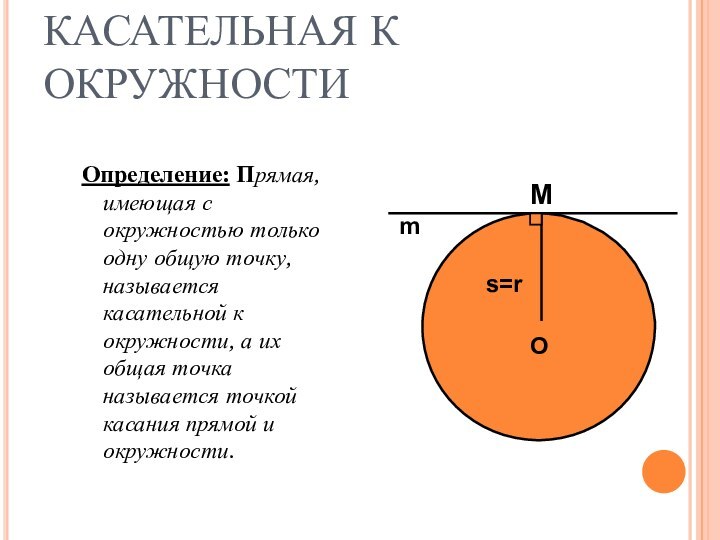
s=r
M
O
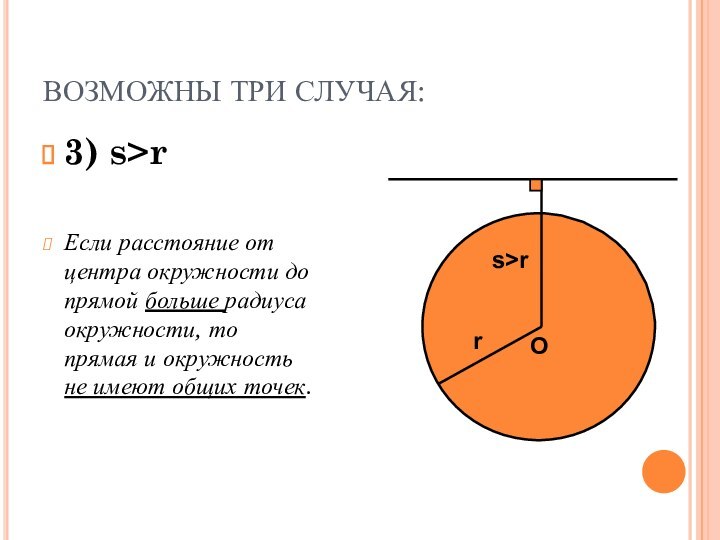
s>r
r
O
s=r
M
m
O
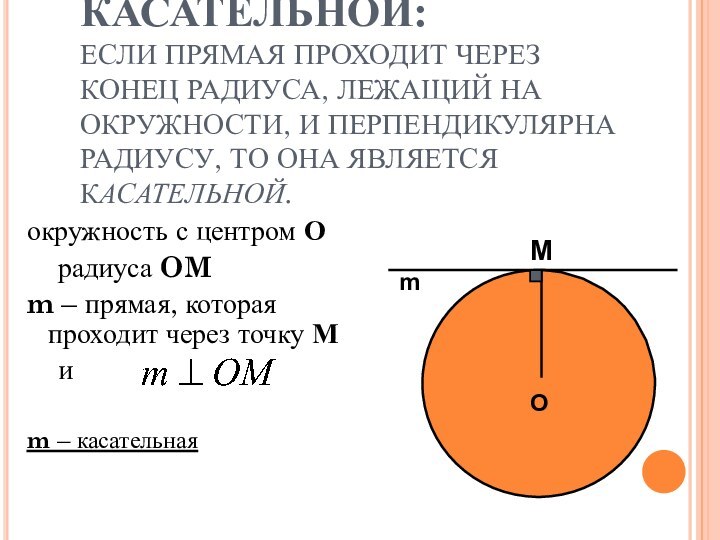
M
m
O
M
m
О
В
С
А
1
2
3
4
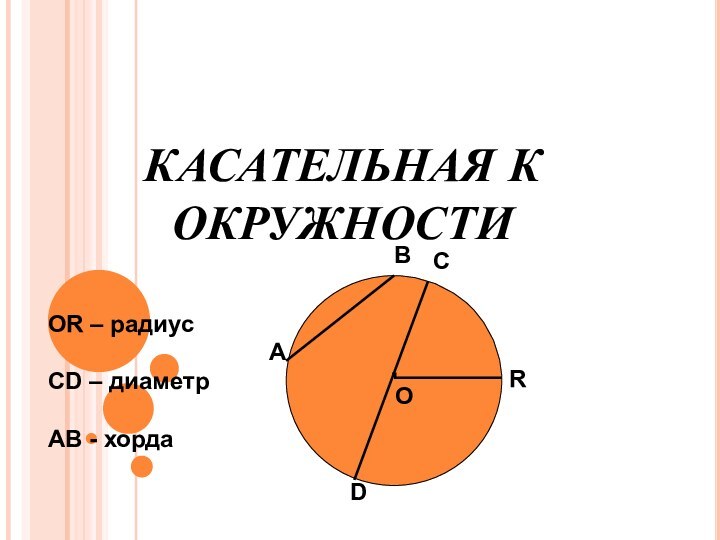
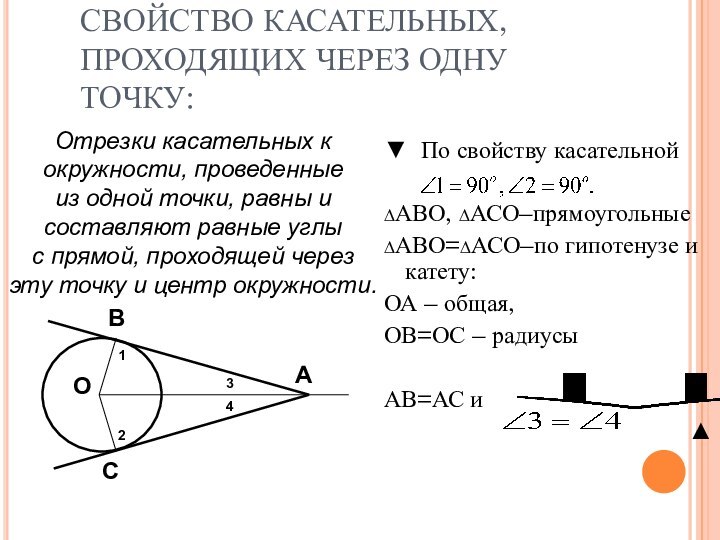
Отрезки касательных к
окружности, проведенные
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.
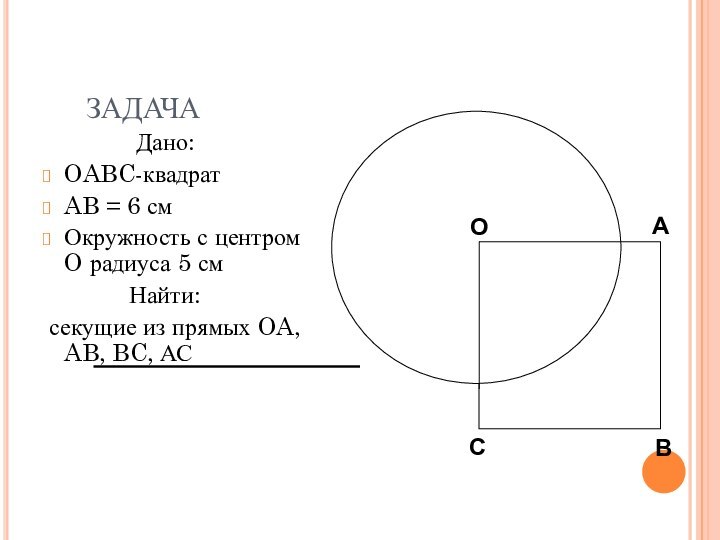
О
А
В
С
О