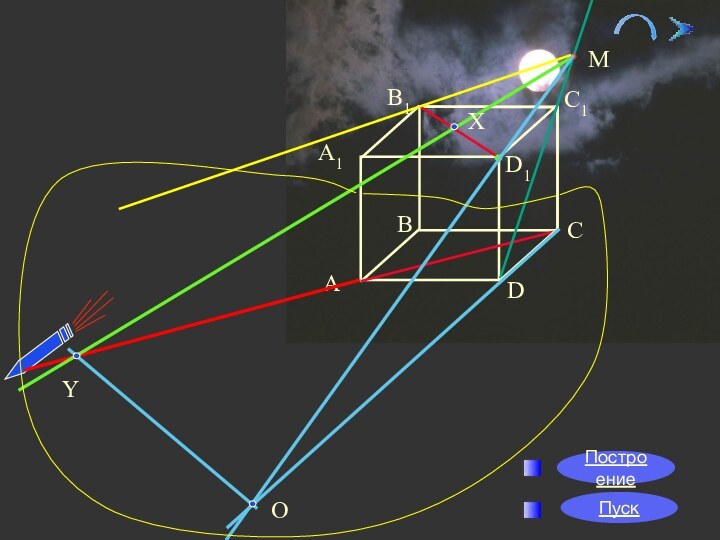
пространство. Объект изучения – скрещивающиеся прямые.
Вы конечно помните, что
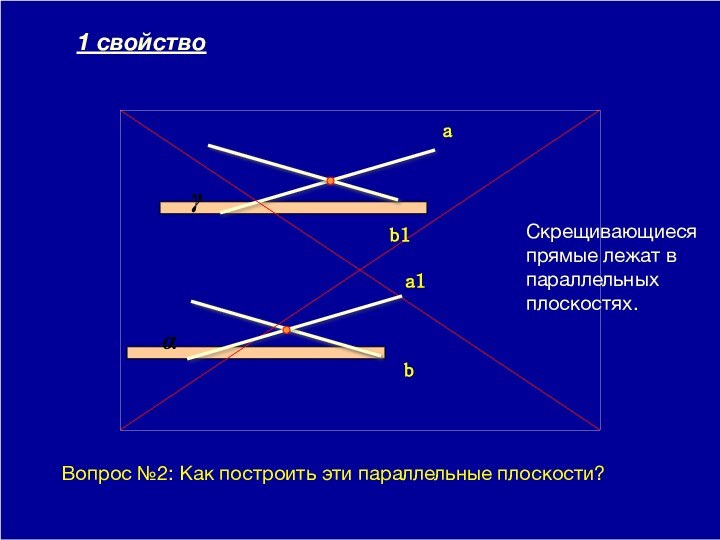
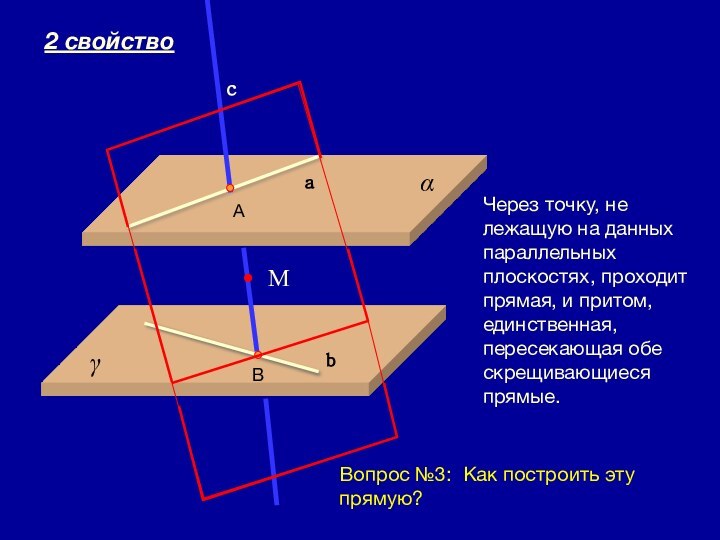
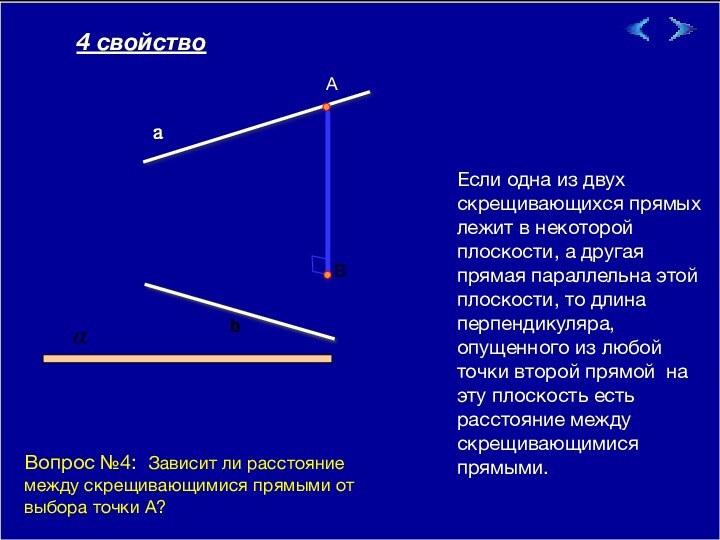
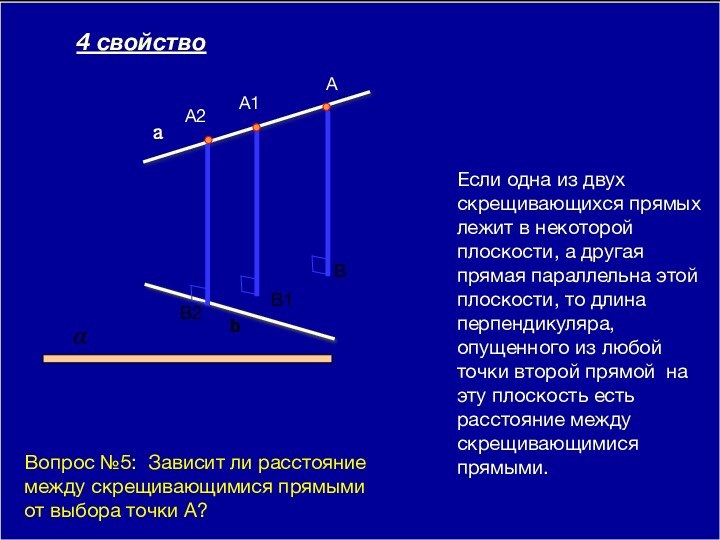
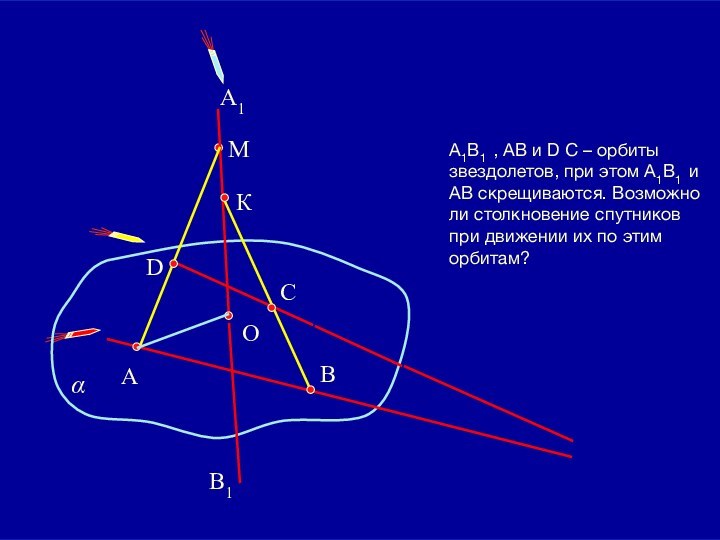
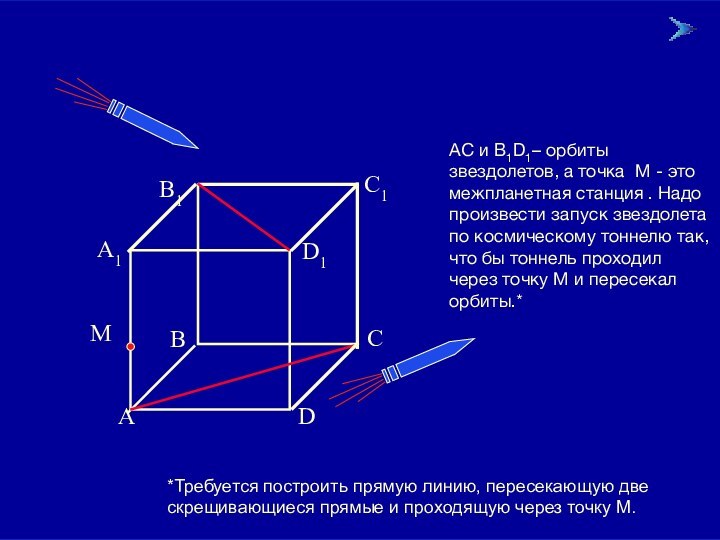
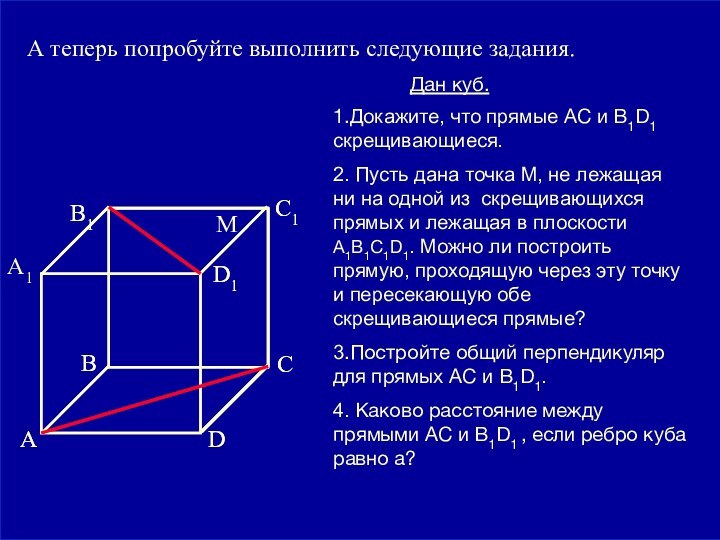
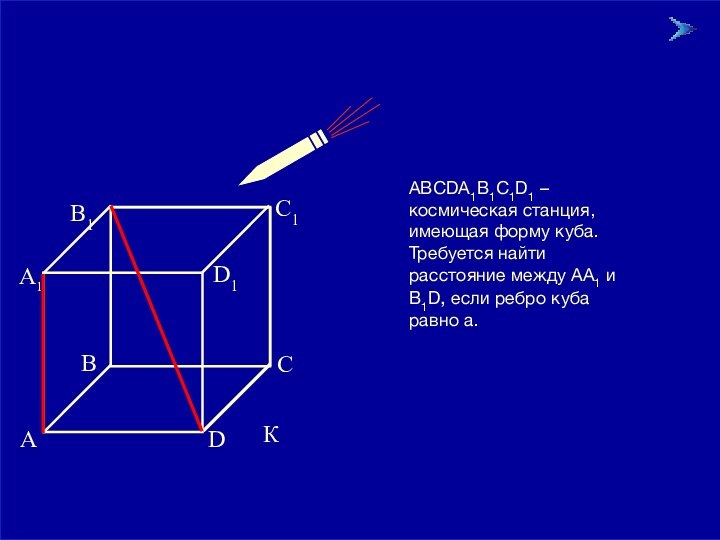
две прямые называются скрещивающимися, если они не лежат в одной плоскости.Давайте посмотрим какими еще интересными свойствами обладают скрещивающиеся прямые.