- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Применение теоремы Пифагора в решении практических задач. Подготовка к ОГЭ.
Содержание
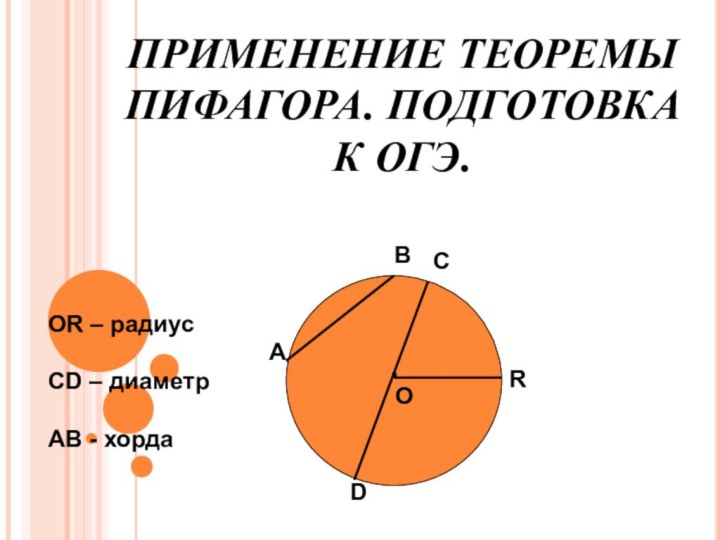
- 2. ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА. ПОДГОТОВКА К ОГЭ..ОАВСDRОR – радиусСD – диаметрAB - хорда
- 3. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИОпределение: Прямая, имеющая с окружностью
- 4. СВОЙСТВО КАСАТЕЛЬНОЙ: КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ ПЕРПЕНДИКУЛЯРНА К
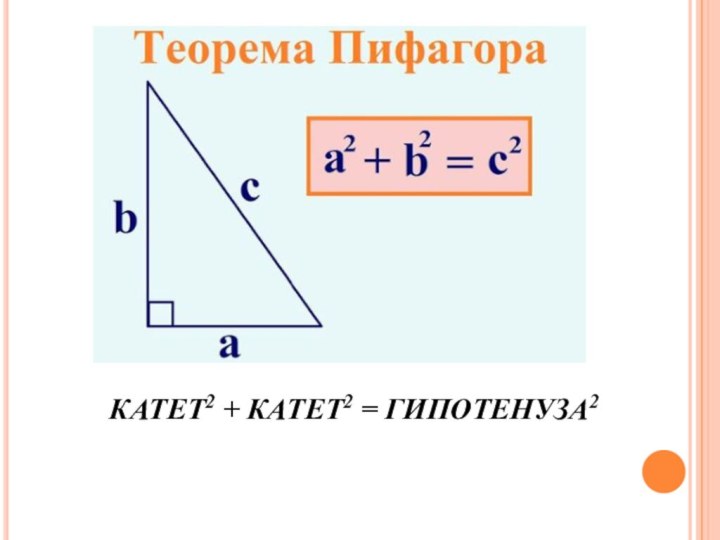
- 5. КАТЕТ2 + КАТЕТ2 = ГИПОТЕНУЗА2
- 6. РЕШЕНИЕ ЗАДАЧ1. К окружности с центром в
- 7. Решение:ДП: проведем ОВ (радиус).ОВ АВ.Треугольник
- 8. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ.2. К окружности с центром
- 9. Решение:ДП: проведем ОВ (радиус).Треугольник АОВ – прямоугольный.По
- 10. 3. Отрезок AB = 40 касается окружности радиуса 30 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
- 11. Решение: AD = ?ОВ АВ
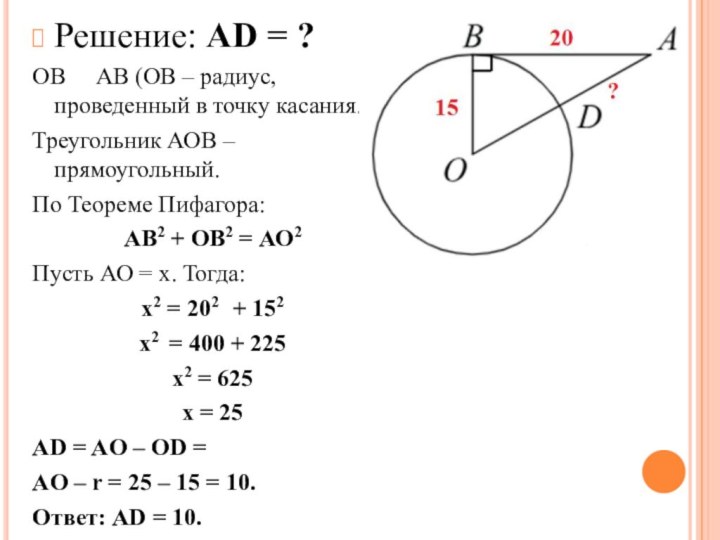
- 12. 4. Отрезок AB = 20 касается окружности радиуса 15 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
- 13. Скачать презентацию
- 14. Похожие презентации
ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА. ПОДГОТОВКА К ОГЭ..ОАВСDRОR – радиусСD – диаметрAB - хорда



Слайд 3
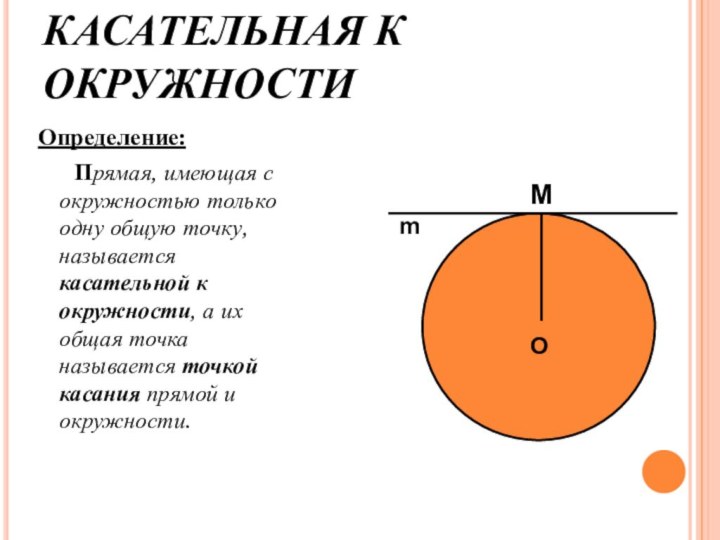
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Определение:
Прямая, имеющая с окружностью только
одну общую точку, называется касательной к окружности, а их
общая точка называется точкой касания прямой и окружности.O
M
m
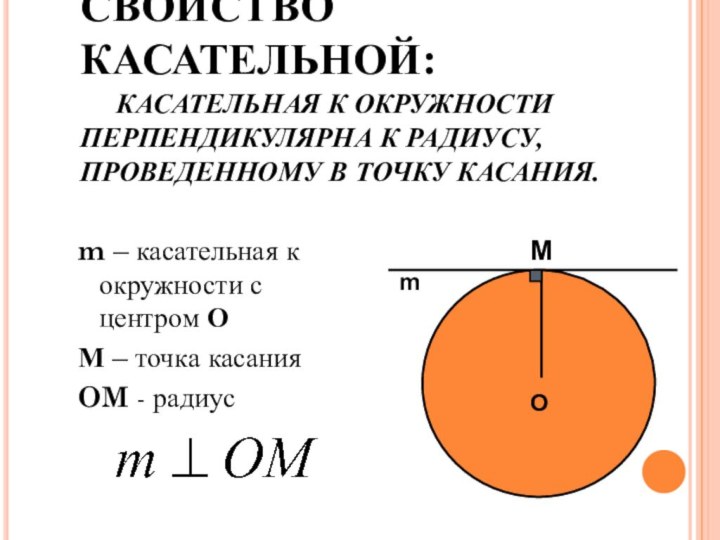
Слайд 4 СВОЙСТВО КАСАТЕЛЬНОЙ: КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ ПЕРПЕНДИКУЛЯРНА К РАДИУСУ, ПРОВЕДЕННОМУ
В ТОЧКУ КАСАНИЯ.
m – касательная к окружности с центром
ОМ – точка касания
OM - радиус
O
M
m
Слайд 6
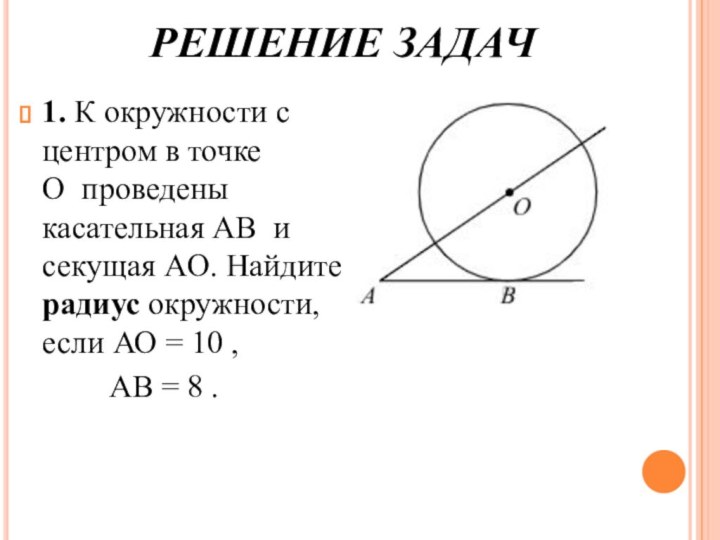
РЕШЕНИЕ ЗАДАЧ
1. К окружности с центром в точке
О проведены касательная AB и секущая AO. Найдите радиус окружности, если АО
= 10 ,АВ = 8 .
Слайд 7
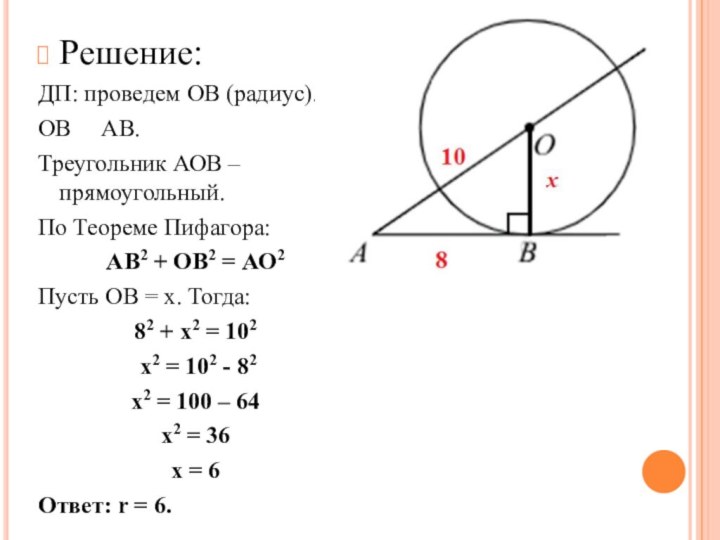
Решение:
ДП: проведем ОВ (радиус).
ОВ АВ.
Треугольник АОВ
– прямоугольный.
По Теореме Пифагора:
АВ2 + ОВ2 = АО2
Пусть
ОВ = х. Тогда:82 + х2 = 102
х2 = 102 - 82
х2 = 100 – 64
х2 = 36
х = 6
Ответ: r = 6.
Слайд 8
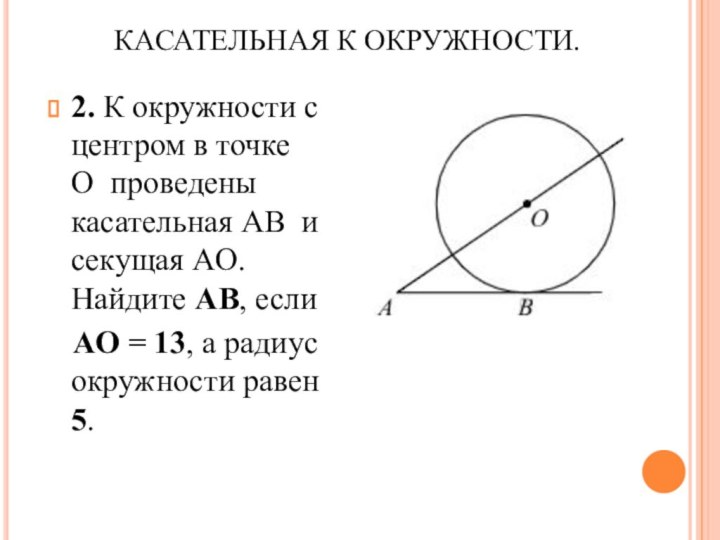
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ.
2. К окружности с центром в
точке О проведены касательная AB и секущая AO. Найдите АВ, если
АО = 13, а радиус окружности равен 5.
Слайд 9
Решение:
ДП: проведем ОВ (радиус).
Треугольник АОВ – прямоугольный.
По Теореме
Пифагора:
АВ2 + ОВ2 = АО2
Пусть АВ = х.
Тогда:х2 + 52 = 132
х2 = 132 - 52
х2 = 169 - 25
х2 = 144
х = 12
Ответ: АВ = 12.
Слайд 10
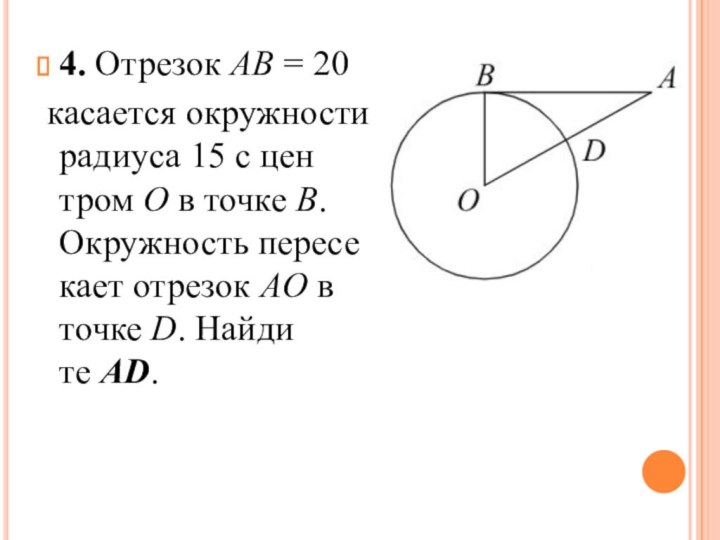
3. Отрезок AB = 40
касается окружности радиуса 30 с центром O в
точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Слайд 11
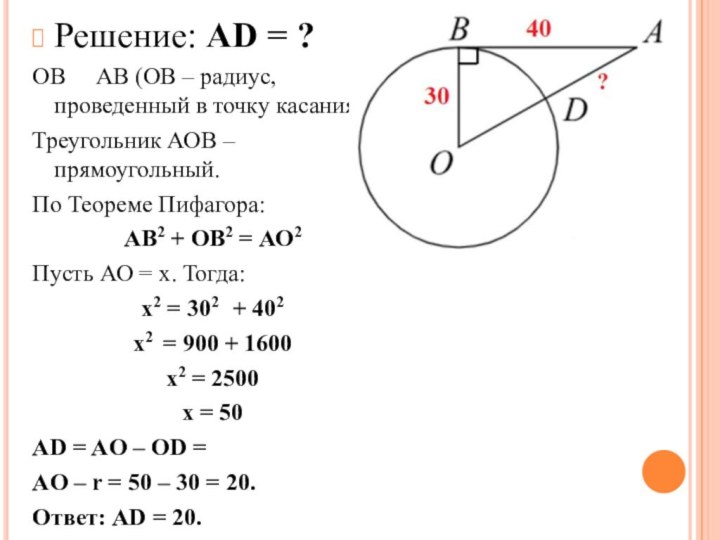
Решение: AD = ?
ОВ АВ (ОВ
– радиус, проведенный в точку касания.)
Треугольник АОВ – прямоугольный.
По
Теореме Пифагора:АВ2 + ОВ2 = АО2
Пусть АО = х. Тогда:
х2 = 302 + 402
х2 = 900 + 1600
х2 = 2500
х = 50
AD = AO – OD =
AO – r = 50 – 30 = 20.
Ответ: АD = 20.