Презентация на тему по теме треугольники для итогового повторения в 9 классе

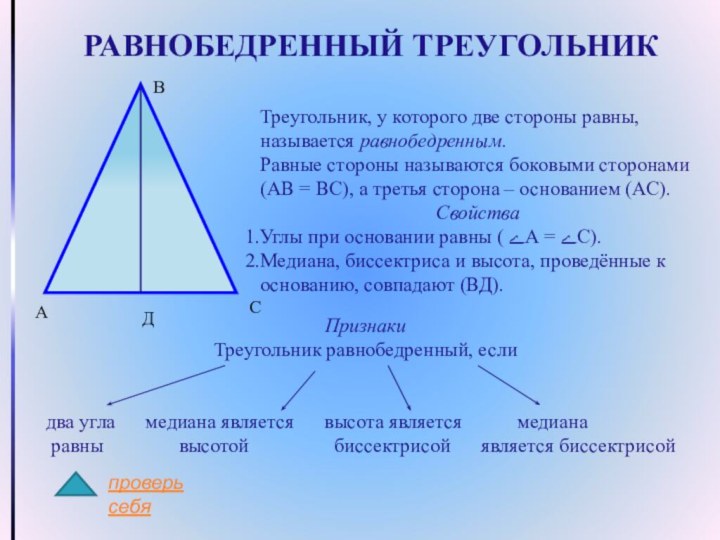
равнобедренным.
Равные стороны называются боковыми сторонами (АВ = ВС), а

третья сторона – основанием (АС).
Свойства
Углы при основании равны ( ےА = ےС).
Медиана, биссектриса и высота, проведённые к основанию, совпадают (ВД).

В

А

С

Д

Признаки
Треугольник равнобедренный, если


два угла медиана является высота является медиана
равны высотой биссектрисой является биссектрисой

проверь себя

равносторонним (правильным).
Свойства
Все углы равны ( ےА = ےВ =

ےС).
Каждая медиана совпадает с биссектрисой и высотой, проведёнными из той же вершины (ВД).
Центры вписанной и описанной окружностей совпадают.

В

А

С

Д

О

r

R

а

ОД = r =

=

ОВ = R =

=

R = 2r

h =

S =

=

=

R =

r =

а

b

с

β

γ

1800

α

α +β + γ = 1800

Против большей стороны в треугольнике лежит больший угол

а > b ↔ α > β

Любая сторона треугольника меньше суммы двух других сторон, но больше модуля их разности │а – b │< c < a + b

α

β

δ

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним

δ = α + β

проверь себя

проверь себя

I признак

)

)

По двум сторонам и углу между ними

II признак

III признак

)

)

)

)

)

)

По одной стороне
и двум прилежащим
к ней углам

По трём сторонам

А

В

М

N

С

P

ΔАВС ∞ ΔMNP

1. ےА = ےМ ے В = ےN

2. ےA = ےM

3.

отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника.

Каждая медиана делит треугольник на 2 равновеликих треугольника
(одинаковой площади).
Три медианы пересекаются в одной точке, которая всегда находится внутри треугольника (центр масс треугольника). Медианы точкой пересечения делятся в отношении 2:1, считая от вершины треугольника.

а

b

с

а

b

с

отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой

на противолежащей стороне.
Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам:

а

b

с

(

(

Три биссектрисы пересекаются в одной точке, которая всегда лежит внутри треугольника. Эта точка является центром вписанной окружности.

проверь себя

перпендикуляр, проведённый из этой вершины к прямой , содержащей

противолежащую сторону треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром.

а

b

с

Ортоцентр остроугольного треугольника лежит внутри треугольника. Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла. Ортоцентр тупоугольного треугольника лежит вне треугольника. Высоты треугольника обратно пропорциональны его сторонам:

¬

¬

¬

треугольника и равна её половине:

MN ║AC , MN

= AC.

Она отсекает треугольник, подобный данному, с коэффициентом подобия

В

А

С

M

N

которого обозначены a, b, c, а величины противолежащих им

углов

а

b

с

β

γ

α

α, ,

β,

γ,

справедливы две теоремы.
Теорема косинусов:

Теорема синусов:

где R - радиус описанной окружности

a, b, c, а высота

а

b

с

¬

В

С

А

площади вычисляются по формулам:

S =

S =

β

S =

S =

, где r – радиус вписанной окружности

, где

S =

, где R – радиус описанной окружности

(формула Герона)

p =

а
b

О

r

c

В любой треугольник можно вписать окружность.
Центр вписанной окружности – точка пересечения биссектрис.

, где S площадь треугольника, а

p =

L

L

A

B

C

M

L

N

p-a

p-a

p-b

p-c

p-b

p-c