- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тригонометрия.
Содержание
- 2. Тригономе́трия (от греч. τρίγονο (треугольник)
- 3. Разделы тригонометрии. Тригонометрия делится на плоскую, или
- 4. Основные формулы плоской тригонометрии Пусть а, b,
- 5. Основные формулы плоской тригонометрииТеорема синусов:
- 6. Основные формулы плоской тригонометриитеорема косинусов:a2 = b2 + c2 — 2bc cos A,Теорема косинусов:
- 7. Основные формулы плоской тригонометрииТеорема тангенсов:
- 8. Основные формулы плоской тригонометрииПлощадь треугольника:
- 9. Основные формулы плоской тригонометрииУглы треугольника, если известны
- 10. История создания.Для компенсации отсутствия таблицы хорд математики
- 11. Первые тригонометрические таблицы были, вероятно, составлены Гиппархом
- 12. Менелай Александрийский (100 н. э.) написал «Сферику» в
- 13. Теорема Птолемея, которая говорит о том, что
- 14. Плоская тригонометрия начала развиваться позже
- 15. Другие источники сообщают,
- 16. Тригонометрические функции угла θ внутри единичной окружностиСинус —
- 17. Данные определения позволяют вычислить значения функций для
- 18. ПрименениеТригонометрические вычисления применяются практически во всех областях
- 19. Скачать презентацию
- 20. Похожие презентации
Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название


















Слайд 3
Разделы тригонометрии.
Тригонометрия делится на плоскую, или прямолинейную,
и сферическую тригонометрию. Теория тригонометрических функций (гониометрия) и её
приложения к решению плоских прямоугольных и косоугольных треугольников изучаются в средней школе
Слайд 4
Основные формулы плоской тригонометрии
Пусть а, b, с
— стороны треугольника, А, В, С — противолежащие им
углы (А+В+С = p), ha, hb, hc — высоты, 2p — периметр, S — площадь, 2R — диаметр окружности, описанной около треугольника.
Слайд 6
Основные формулы плоской тригонометрии
теорема косинусов:
a2 = b2 +
c2 — 2bc cos A,
Теорема косинусов:
Слайд 9
Основные формулы плоской тригонометрии
Углы треугольника, если известны стороны,
могут быть найдены по теореме косинусов или по формулам
вида:
Слайд 10
История создания.
Для компенсации отсутствия таблицы хорд математики времен
Аристарха иногда использовали хорошо известную теорему, в современной записи —
sin α/ sin β < α/β < tan α/ tan β, где 0° < β < α < 90°, совместно с другими теоремами.Слайд 11 Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским
(180—125 лет до н. э.). Гиппарх был первым, кто свёл в
таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд.Слайд 12 Менелай Александрийский (100 н. э.) написал «Сферику» в трёх
книгах. В первой книге он представил основы для сферических
треугольников. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».Слайд 13 Теорема Птолемея, которая говорит о том, что сумма
произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей,
влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха.Слайд 14 Плоская тригонометрия начала развиваться позже сферической,
хотя отдельные теоремы её встречались и раньше. Например, 12-я
и 13-я теоремы второй книги "Начал" Евклида (3 в. дон. э.) выражают по существу теорему косинусов. Плоская тригонометрия получила развитие у аль-Баттани (2-я половина 9 — начало 10 вв.), Абу-ль-Вефа (10 в.), Бхаскара (12 в.) и Насирэддина Туси (13 в.), которым была уже известна теорема синусов. Теорема тангенсов была получена Региомонтаном (15 в.). Дальнейшие работы в области Т. принадлежат Н. Копернику (1-я половина 16 в.), Т. Браге (2-я половина 16 в.), Ф. Виету (16 в.), И. Кеплеру (конец 16 — 1-я половина 17 вв.). Современный вид тригонометрия получила в работах Л. Эйлера (18 в.).Слайд 15 Другие источники сообщают, что
именно замена хорд синусами стала главным достижением Средневековой Индии.
Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
sin2α + cos2α = 1
sin α = cos(90 – α)
sin(α ± β) = sinα cosβ ± sinβ cosα
Индийцы также знали формулы для кратных углов sinn, cosn, где n = 2,3,4,5.
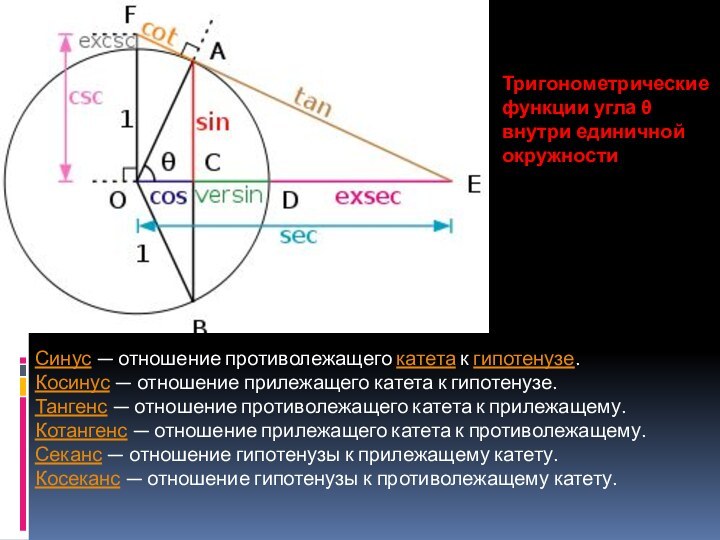
Слайд 16
Тригонометрические функции угла θ внутри единичной окружности
Синус — отношение
противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к
гипотенузе. Тангенс — отношение противолежащего катета к прилежащему.
Котангенс — отношение прилежащего катета к противолежащему.
Секанс — отношение гипотенузы к прилежащему катету.
Косеканс — отношение гипотенузы к противолежащему катету.
Слайд 17 Данные определения позволяют вычислить значения функций для острых
углов, то есть от 0° до 90° (от 0
до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол θ (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:Синус угла θ определяется как ордината точки A.
Косинус — абсцисса точки A.
Тангенс — отношение синуса к косинусу.
Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).
Секанс — величина, обратная косинусу.
Косеканс — величина, обратная синусу.
Для острых углов новые определения совпадают с прежними.





























