Слайд 2
Решите задачу:
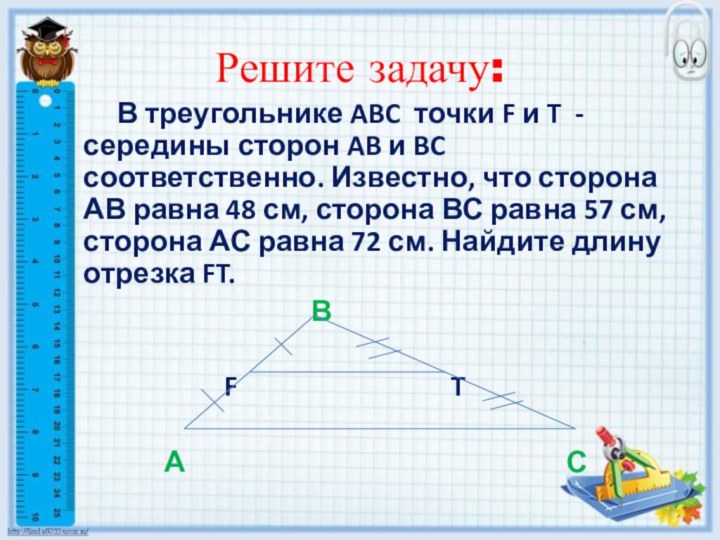
В треугольнике ABC точки
F и T - середины сторон AB и BC
соответственно. Известно, что сторона АВ равна 48 см, сторона ВС равна 57 см, сторона АС равна 72 см. Найдите длину отрезка FT.
В
F T
А С
Слайд 3
Решите задачу:
Пожарную лестницу приставили
к окну, расположенному на высоте 12 м
от земли. Нижний
конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.
12
5
Слайд 4
Тема урока:
Теорема Пифагора.
Цель урока:
сформулировать и доказать
теорему Пифагора, учиться применять теорему Пифагора при решении задач
на нахождение неизвестных сторон прямоугольного треугольника.
Слайд 5
Теоретическая разминка:
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного
треугольника?
Что называется косинусом острого угла в прямоугольном треугольнике?
От чего
зависит косинус острого угла?
Слайд 6
Практическая разминка:
Вычислите: 32; 42; 52; 82; 122; 132;152;202;
252;
Вычислите:√16; √169; √400; √2500.
Решите уравнение:
Х2=25
Х2=9+16
Х2=100-64
Слайд 7
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов его катетов.
Слайд 8
План доказательства:
1. Что дано по условию теоремы?
2.Начертите прямоугольный
треугольник АВС.
3.Что нужно доказать?
4.Опустите высоту из вершины прямого угла
на гипотенузу. Обозначьте основание высоты.
5.Рассмотрите получившиеся треугольники.
6.Выразите косинус угла А. Сколькими способами это можно сделать?
7. Сделайте вывод о двух получившихся отношениях.
8.Примените основное свойство пропорции и запишите получившееся равенство.
9.Аналогично поступите с косинусом угла В.
10 Сложите получившиеся равенства почленно.
11.Преобразуйте алгебраически правую часть равенства.
12. Сделайте вывод.
Повторите доказательство без опоры на план.
Слайд 9
Решите задачу:
Пожарную лестницу приставили
к окну, расположенному на высоте 12 м
от земли. Нижний
конец лестницы отстоит от стены на 5 м. Какова длина лестницы? Ответ дайте в метрах.
12
5
Слайд 10
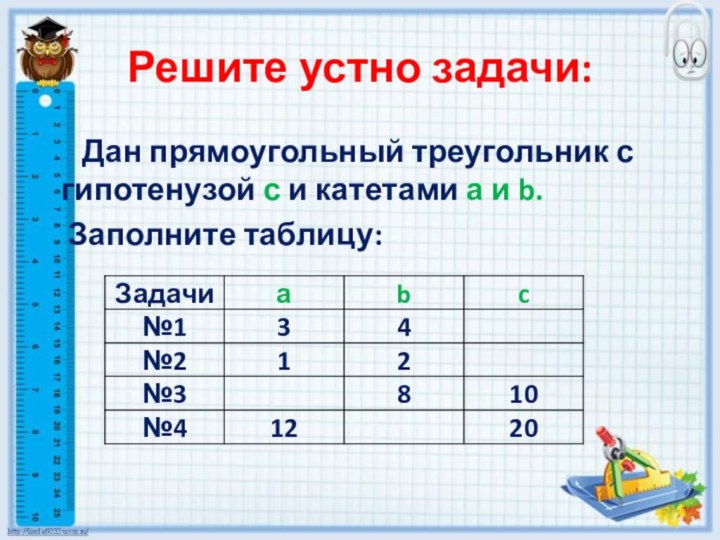
Решите устно задачи:
Дан прямоугольный треугольник с
гипотенузой с и катетами а и b.
Заполните таблицу:
Слайд 11
Пифагор родился в 570 году на
н.э. Существует легенда, что когда он родился, родителям жрица-прорицательница
сообщила, что дитя принесёт столько пользы и добра людям, сколько не приносил и не принесёт никто другой.
Пифагору повезло больше, чем другим ученым древности.
О нем сохранились десятки легенд и мифов, правдивых и выдуманных, реальных и вымышленных.
С его именем связано многое в математике и в первую очередь, конечно, теорема, носящая его имя.
Пифагор – один из самых известных ученых, но и самая загадочная личность, человек-символ, философ и пророк.
Слайд 12
Пифагор имел красивую внешность, ростом он был 180
см., носил длинную бороду, а на голове золотую диадему.
В возрасте 60 лет Пифагор женился на своей ученице Феано, девушке удивительной красоты, покорившей сердце мудрого философа своей чистой и пламенной любовью, преданностью и верой.
Слайд 13
Рассказывают, что когда Пифагор
доказал свою знаменитую теорему, он
отблагодарил богов, принеся жертву
сто быков. И поэтому её ещё
называют теоремой «100 быков».
Слайд 14
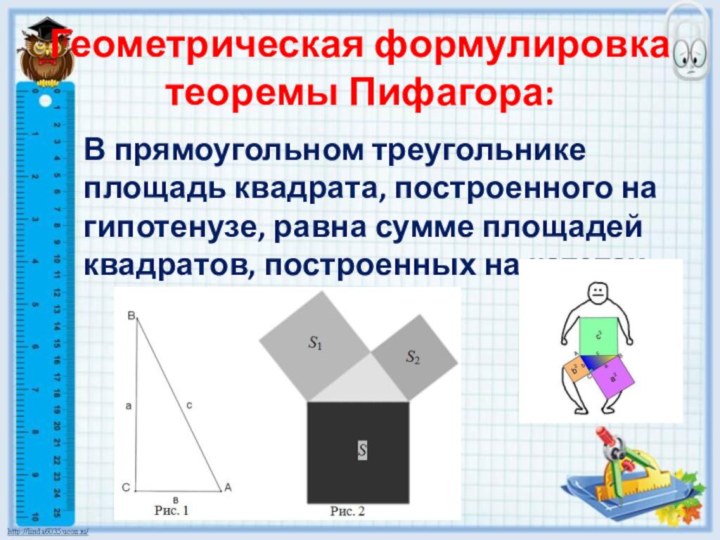
Геометрическая формулировка теоремы Пифагора:
В прямоугольном треугольнике площадь квадрата,
построенного на гипотенузе, равна сумме площадей квадратов, построенных на
катетах.
Слайд 15
В средние века знание теоремы Пифагора говорило о
хорошем уровне математических знаний, а характерный чертеж к ней,
который школьниками превращается, например, в облеченного в мантию профессора, становился символом математики.
Слайд 16
Заповеди Пифагора актуальны и сейчас:
1. Делать то, что
в последствии не огорчит тебя и не принудит раскаиваться;
2.
Не делай никогда того, что не знаешь, но научиcь всему, что следует знать;
3. Не пренебрегай здоровьем своего тела;
4. Приучайся жить просто и без роскоши.