Презентация на тему по геометрии на тему Второй и третий признаки равенства треугольников

одного треугольника соответственно равны стороне и двум прилегающим к

ней углам другого треугольника, то такие треугольники равны.

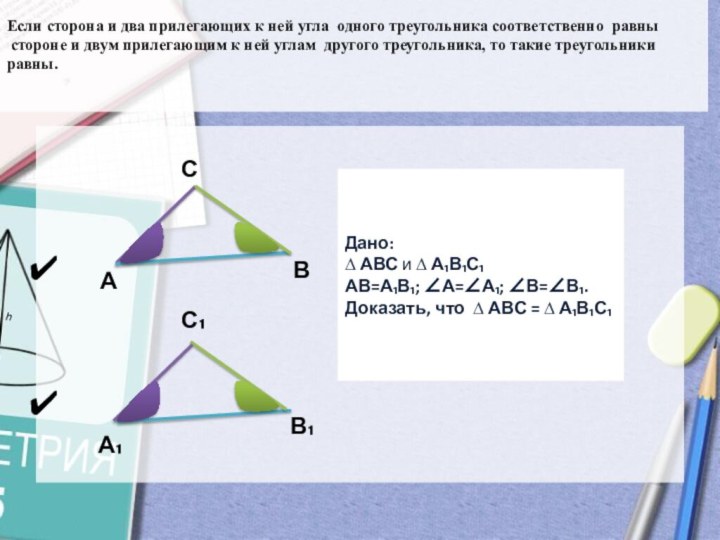
Дано:
∆ АВС и ∆ А₁В₁С₁
АВ=А₁В₁; А=А₁; В=В₁.
Доказать, что ∆ АВС = ∆ А₁В₁С₁

А

В

С

В₁

А₁

С₁

ВС - на
В₁С₁. Вершина С окажется лежащей как на

луче А₁С₁ так и на луче В₁С₁, то есть совместится с общей точкой этих лучей – вершиной С₁. Значит, совместятся стороны АС и А₁С₁, ВС и В₁С₁, => ∆АВС и ∆А₁В₁С₁ полностью совместятся, т.е. они равны. Ч.т.д.

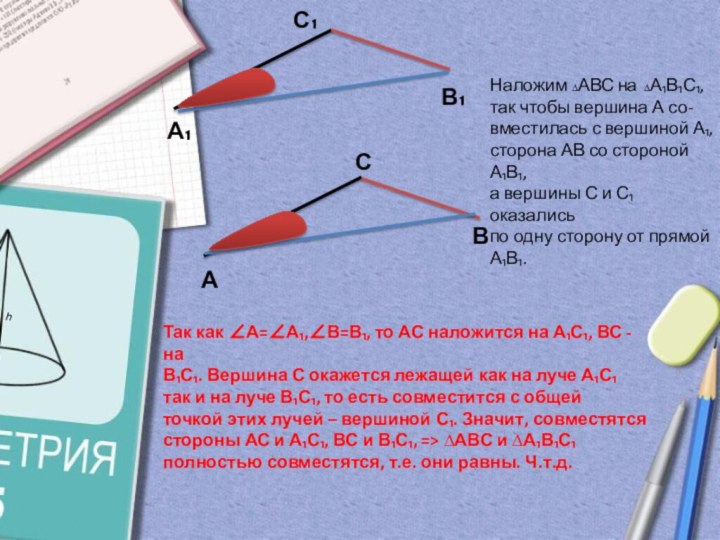
Наложим ∆АВС на ∆А₁В₁С₁,
так чтобы вершина А со-
вместилась с вершиной А₁,
сторона АВ со стороной А₁В₁,
а вершины С и С₁ оказались
по одну сторону от прямой
А₁В₁.

А

С

В

А₁

В₁

С₁

по свойству
биссектрисы
Следовательно,
∆АВС=∆АDС ч.т.д.
2
1
А
B
C
D

2+4 =С
3.1=2, по условию, =>

∆АВС=∆DCB.

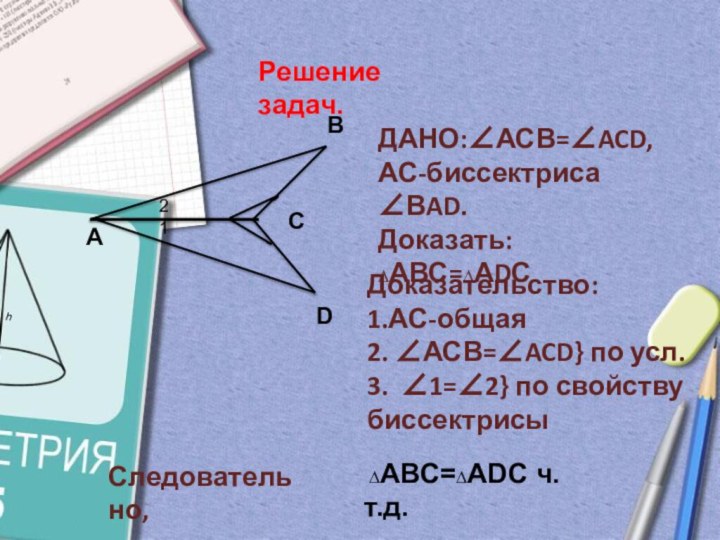
Рассмотрим ∆ВОС- равнобедренный, т.к. 1=2
(по условию), 1.ВО=ОС
2.3=4 (по условию)
3.АВ=СD (т.к. ∆АВС=∆DСВ)=>
∆АВО=∆DCO по 1 признаку равенства
треугольников

1

О

В

С

А

D

2

4

3

сторонам другого
треугольника, то такие треугольники равны.
Дано: ∆АВС, ∆А₁В₁С₁,
АВ=₁А₁В₁,

ВС=В₁С₁, АС=А₁С₁.
Доказать: ∆АВС=∆А₁В₁С₁

Доказательство:
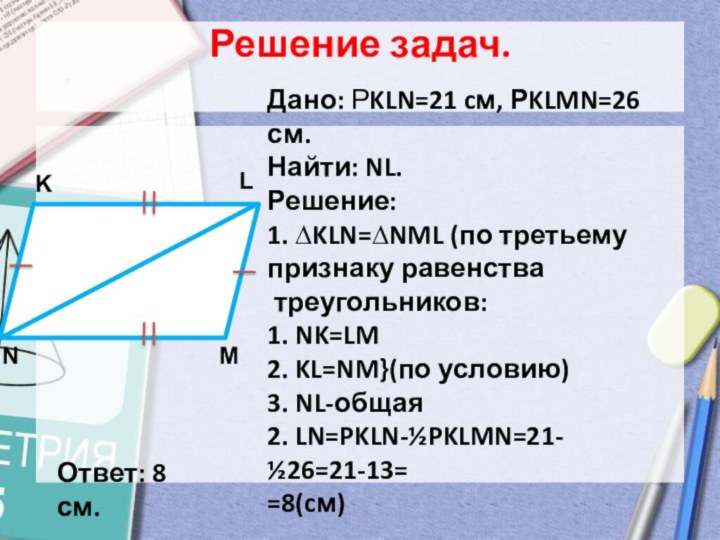
Приложим ∆АВС к ∆А₁В₁С₁ так, чтобы вершина А совместилась с вершиной А1, вершина В – с вершиной В1, а вершины С и С1 оказались по разные стороны от прямой А1В1.

А

С

В

В₁

С₁

А₁

∆А₁С₁С и

∆СВ₁С₁- равнобедренные,
=>1=2;3=4; А1СВ1=А₁С₁ В₁.
Итак, АС=А1С1, ВС=В1С1 , С= С1. . =>, ∆АВС=∆А₁В₁С₁ ( по первому
признаку равенства
треугольников)

Возможны три случая:

А₁(А)

В₁(В)

С

С₁

1

2

3

4

1. случай