Слайд 2
Что такое "правильные многогранники"?
Слайд 3
Многогранник называется правильным, если:
1). он выпуклый,
2). все
его грани - равные правильные многоугольники,
3). в каждой
вершине сходится одинаковое число граней,
4). все его двухгранные углы равны.
Слайд 4
Существует всего 5 видов правильных многогранников:
правильный тетраэдр
правильный октаэдр
правильный икосаэдр
куб
правильный додекаэдр
Слайд 5
Правильный тетраэдр
Тетраэдр составлен из четырех равносторонних треугольников.
Каждая его вершина является вершиной трех треугольников. Тетраэдр имеет
4 грани, 4 вершины и 6 ребер.
Слайд 6
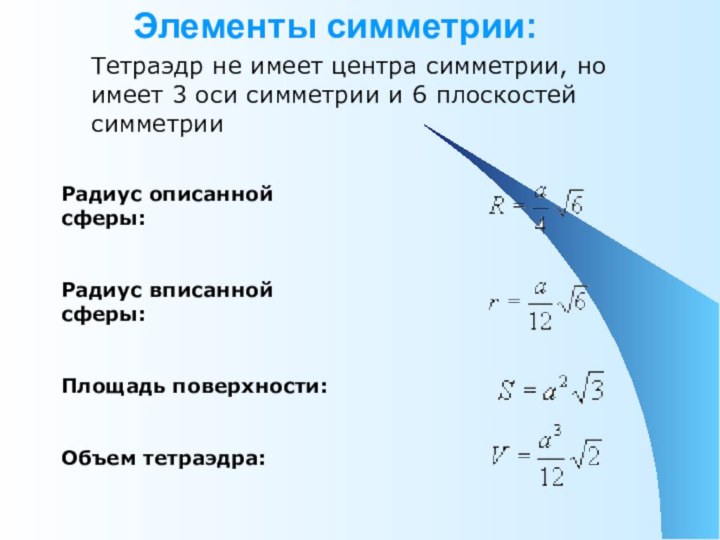
Элементы симметрии:
Тетраэдр не имеет центра
симметрии, но имеет 3 оси симметрии и 6 плоскостей
симметрии
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем тетраэдра:
Слайд 7
Правильный октаэдр.
Октаэдр составлен из восьми равносторонних треугольников.
Каждая его вершина является вершиной четырех треугольников. октаэдр имеет
8 граней, 6 вершин и 12 ребер.
Слайд 8
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра,
9 осей симметрии и 9 плоскостей симметрии.
Радиус
описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
Слайд 9
Правильный икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая
его вершина является вершиной пяти треугольников. Икосаэдр имеет 20
граней, 12 вершин и 30 ребер.
Слайд 10
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра,
15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
Слайд 11
Куб
Куб составлен из шести квадратов. Каждая его вершина
является вершиной трех квадратов. Куб имеет 6 граней, 8
вершин и 12 ребер.
Слайд 12
Элементы симметрии:
Куб имеет центр симметрии - центр куба,
9 осей
симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
Объем куба:
S =6a2
V =a3
Слайд 13
Правильный додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
его вершина является вершиной трех пятиугольников. Додекаэдр имеет 12
граней, 20 вершин и 30 ребер.
Слайд 14
Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра,
15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
Слайд 16
Свойства правильных многогранников изу-
чали ученые и священники; их
мо-
дели можно увидеть в работах ар-
хитекторов и ювелиров, им
припи-
сывались различные магические и
целебные свойства.
Слайд 17
Тела Платона
Пять перечисленных выше правильных многогранников часто называют
также «телами Платона» . Великий древнегреческий ученый Платон, живший
в IV-V вв. до н. э., считал, что эти тела олицетворяют сущность природы. Человечеству были известны четыре сущности: огонь, вода, земля и воздух. По мнению Платона, их атомы имели вид правильных многогранников: огня — тетраэдр, земли — гексаэдр, воздуха - октаэдр, воды — икосаэдр. Но оставался еще додекаэдр — отсутствует полное соответствие. Платон предположил, что существует еще одна сущность- мировой эфир, атомы которого имеют вид додекаэдра.
Слайд 18
Архимедовы тела
Множество архимедовых тел можно разбить на несколько

групп.
Первую из них составят пять многогранников, которые получаются
из платоновых тел в результате их усечения. Так могут быть получены пять архимедовых тел: усечённый тетраэдр, усечённый гексаэдр (куб), усечённый октаэдр, усечённый додекаэдр и усечённый икосаэдр.
Другую группу составляют всего два тела, именуемых также квазиправильными многогранниками. Эти два тела носят названия:кубооктаэдр и икосододекаэдр
Два последующих многогранника называются ромбокубооктаэдром и ромбоикосододекаэдром. Иногда их называют также «малым ромбокубооктаэдром» и «малым ромбоикосододекаэдром» в отличие от большого ромбокубооктаэдра и большого ромбоикосододекаэдра.
Наконец существуют две так называемые «курносые» модификации — одна для куба, другая — для додекаэдра. Для каждой из них характерно несколько повёрнутое положение граней, что даёт возможность построить два различных варианта одного и того же «курносого» многогранника (каждый из них представляет собой как бы зеркальное отражение другого).
Слайд 19
Космологическая гипотеза Кеплера
Весьма оригинальна космологическая гипотеза Кеплера, в
которой он попытался связать некоторые свойства Солнечной системы со
свойствами правильных многогранников.
Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел.
Слайд 20
Космологическая гипотеза Кеплера
Вокруг сферы Меркурия, ближайшей к Солнцу
планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры,
вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.
Позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута.
Слайд 22
Правильные многогранники – самые выгодные фигуры, поэтому они
широко распространены в природе. Подтверждением тому служит форма некоторых
кристаллов.
Например, кристаллы поваренной соли имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] × 12H2O), монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.
Слайд 23
Правильные многогранники встречаются так же и в живой
природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по
форме напоминает икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Слайд 24
А теперь попробуйте назвать
многогранники:
тетраэдр
куб
октаэдр
додекаэдр
икосаэдр