- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему урока геометрии в 10 классе по теме: Повторение. Углы и отрезки в окружности
Содержание
- 2. Приветствую вас на уроке геометрииУроки №1-207.09.17г.
- 3. Девиз урокаУспешного усвоения учебного материала
- 4. 07.09.17 Тема урока: Углы и отрезки в окружности. КР
- 5. Цели урока:Повторить все виды углов и отрезков
- 6. Повторение изученного материала
- 7. Назовите дуги, отмеченные на рис.214Какая из этих дуг является большей?Сумма градусных мер этих дуг равна …º1.
- 8. и
- 9. Дуга называется полуокружностью, еслиотрезок, соединяющий её концы является … Назовите на чертеже полуокружности.…- диаметр.Заполните пропуски2.
- 10. Дуга называется полуокружностью, еслиотрезок, соединяющий её концы
- 11. Дуга называется полуокружностью, еслиотрезок, соединяющий её концы является диаметром – полуокружности.АВ – диаметр.и
- 12. Угол с вершиной в центре окружности называется её … углом3.
- 13. Угол с вершиной в центре окружности называется её центральным углом
- 14. Угол с вершиной в центре окружности называется
- 15. Угол с вершиной в центре окружности называется
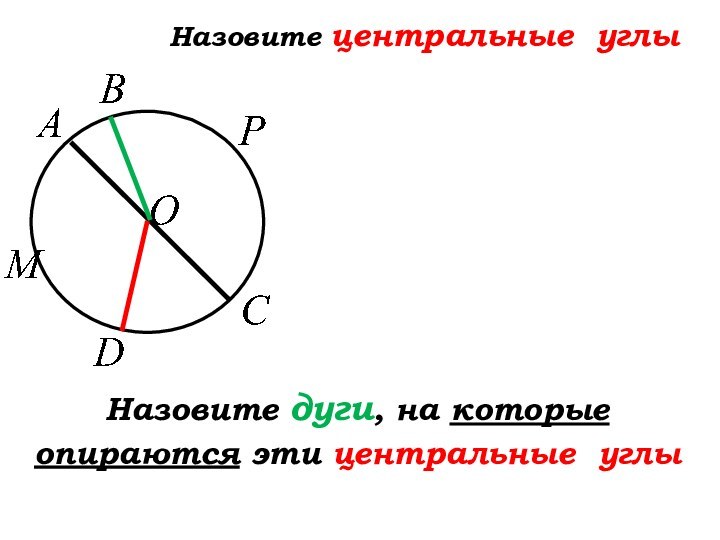
- 16. Назовите центральные углыНазовите дуги, на которые опираются эти центральные углы
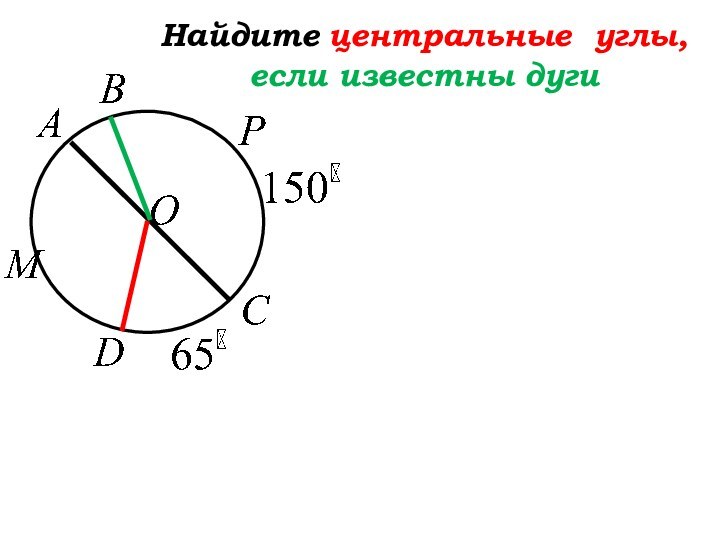
- 17. Найдите центральные углы, если известны дуги
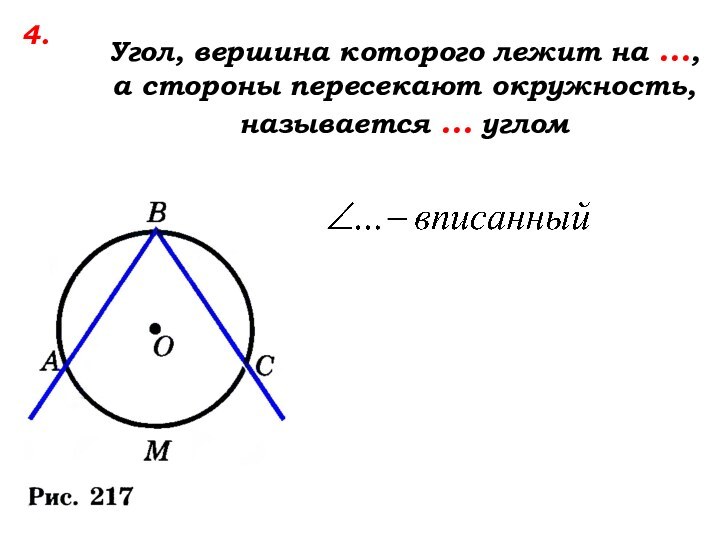
- 18. Угол, вершина которого лежит на …, а стороны пересекают окружность, называется … углом 4.
- 19. Угол, вершина которого лежит на окружности,
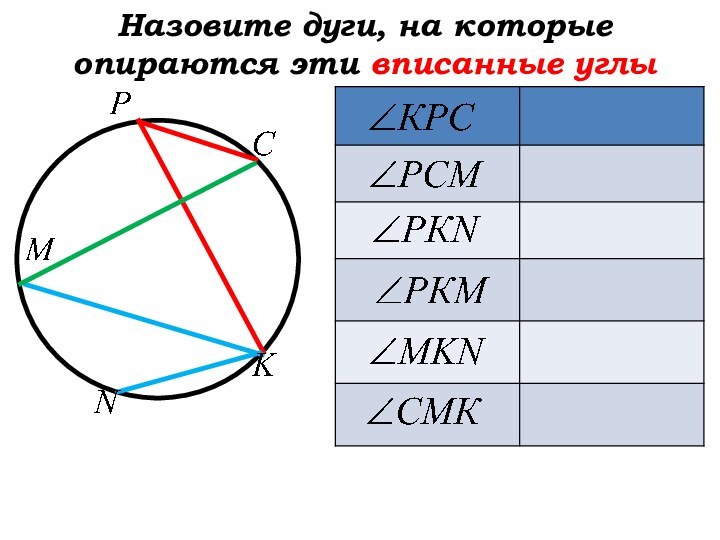
- 20. Назовите дуги, на которые опираются эти вписанные углы
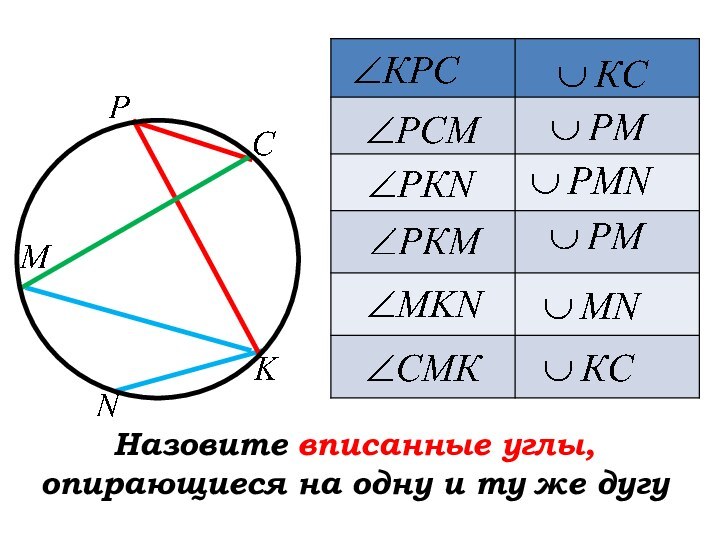
- 21. Назовите вписанные углы, опирающиеся на одну и ту же дугу
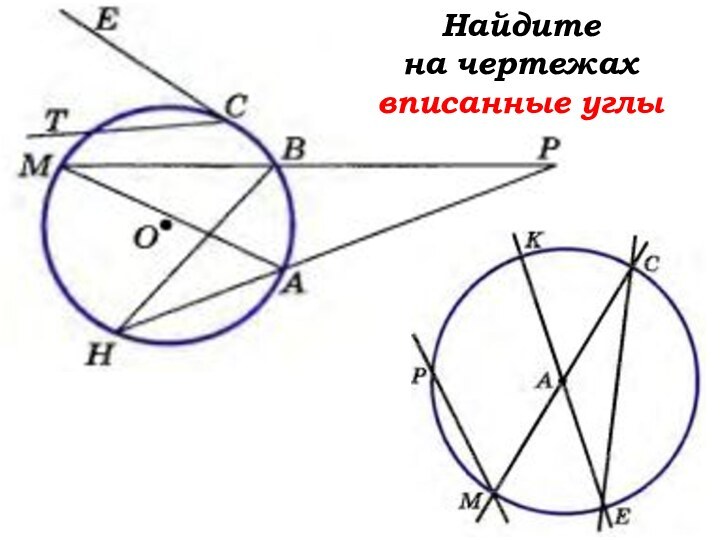
- 22. Найдите на чертежах вписанные углы
- 23. Вывод 1. Центральный угол равен …,
- 24. Вывод 1. Центральный
- 25. Вывод 4. Следствие 1. Вписанные
- 26. Вывод 4. Следствие 1. Вписанные
- 27. 6. Если
- 28. 6. Если
- 29. 7. Угол между …
- 30. 7. Угол между касательной и
- 31. 8. Квадрат касательной равен произведению
- 32. 8. Квадрат касательной равен произведению всей
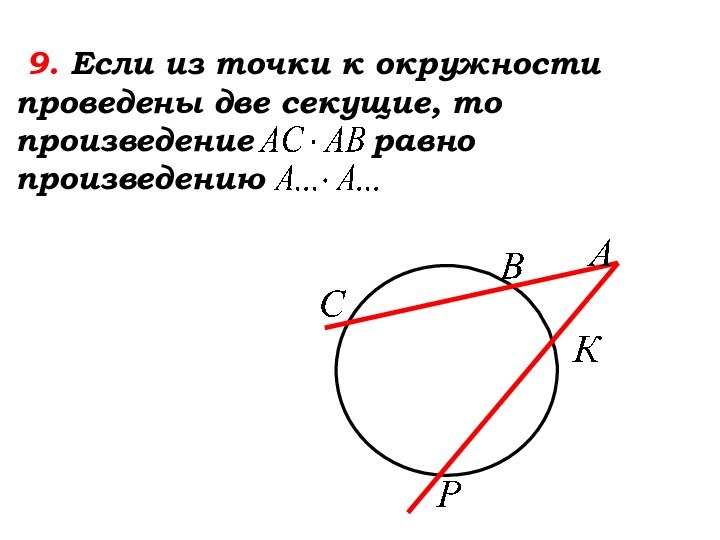
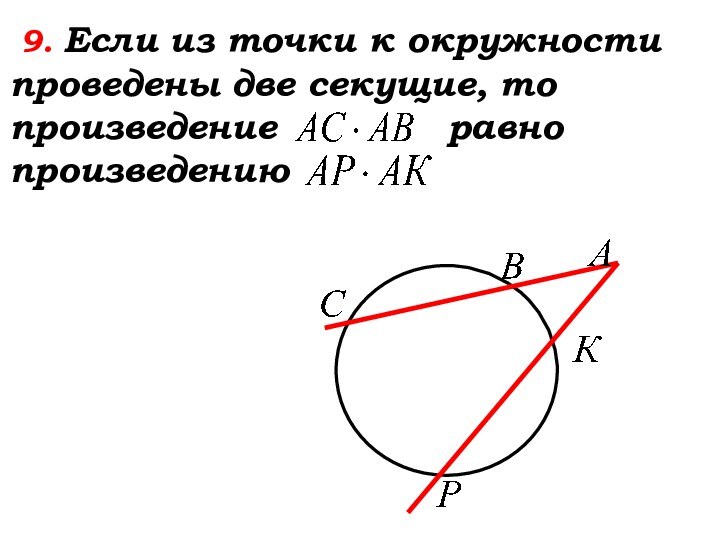
- 33. 9. Если из точки к
- 34. 9. Если из точки к
- 35. 10. Угол, с вершиной вне
- 36. 10. Угол, с вершиной вне
- 37. 11. Если угол образован … …
- 38. 11. Если угол образован двумя пересекающимися
- 39. Решение
- 40. 1. Прочитайте задачу. Выполните чертёж окружности.
- 41. Решение:
- 42. Решение:
- 43. Решение: Максимальный балл за решение - 4б:Верно выполнен чертёж-1б,Верно найдена нужная формула-1бВерно завершено решение-2б
- 44. 1. Выполните чертёж окружности. 2. Отметьте точки. 3. Проведите необходимые по условию отрезки. 4. …
- 45. 1. Выполните чертёж окружности. 2. Отметьте
- 47. Достройте вначале только названный в указаниях треугольник и укажите угол, равныйДорешайте задачу.
- 48. 1. По свойству средней линии треугольника
- 49. Максимальный балл за решение - 4б:Верно
- 50. 12.а)
- 51. а)
- 52. б) Если расстояние
- 53. б) Если расстояние
- 54. в)
- 55. в)
- 56. 13.
- 57. а)
- 58. б)
- 59. б)
- 60. 14.
- 61. Отрезки
- 62. 15. Биссектрисы треугольника … в … точке
- 63. Биссектрисы треугольника пересекаются в одной точкеOK=…=…
- 64. Биссектрисы треугольника пересекаются в одной точкеOK=OL=OMТочка пересечения биссектрис треугольника … от его …
- 65. Биссектрисы треугольника пересекаются в одной точкеOK=OL=OMТочка пересечения биссектрис треугольника равноудалена от его сторон
- 66. 16. Серединные перпендикуляры к … треугольника … в одной точке.
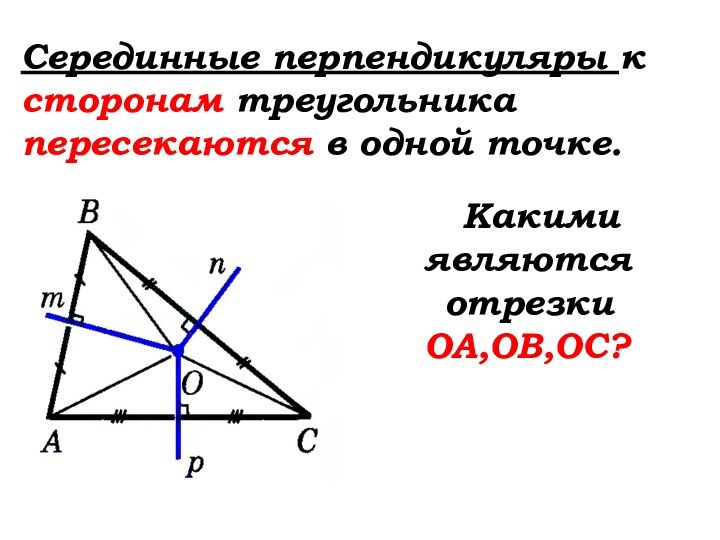
- 67. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Какими являются отрезки OА,OВ,OС?
- 68. Серединные перпендикуляры к сторонам треугольника пересекаются
- 69. Серединные перпендикуляры к сторонам треугольника пересекаются
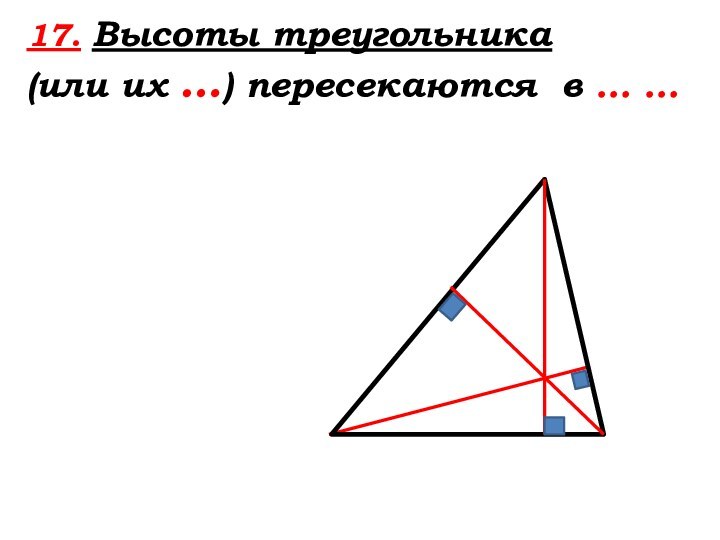
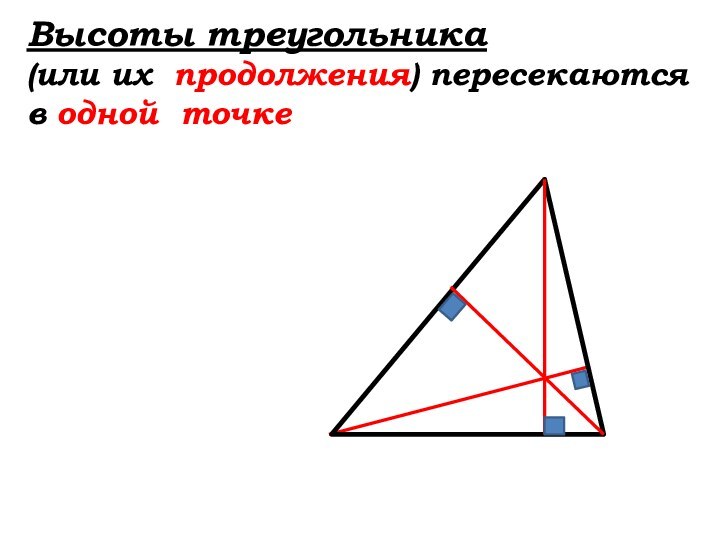
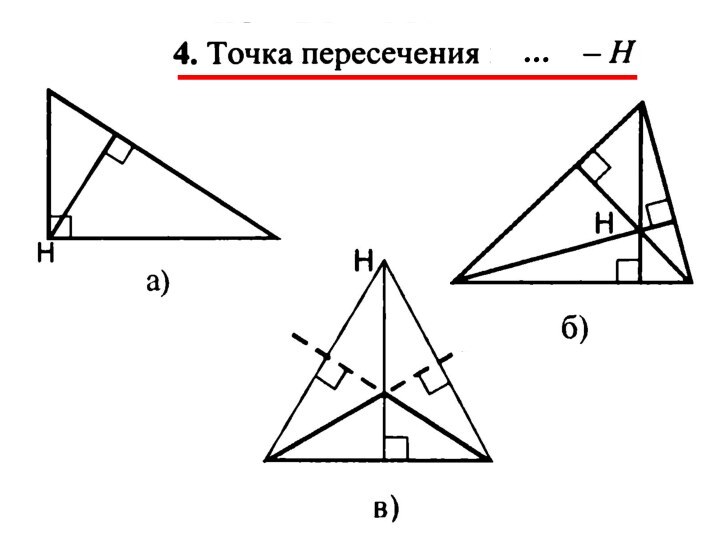
- 70. 17. Высоты треугольника (или их …) пересекаются в … …
- 71. Высоты треугольника (или их продолжения) пересекаются в одной точке
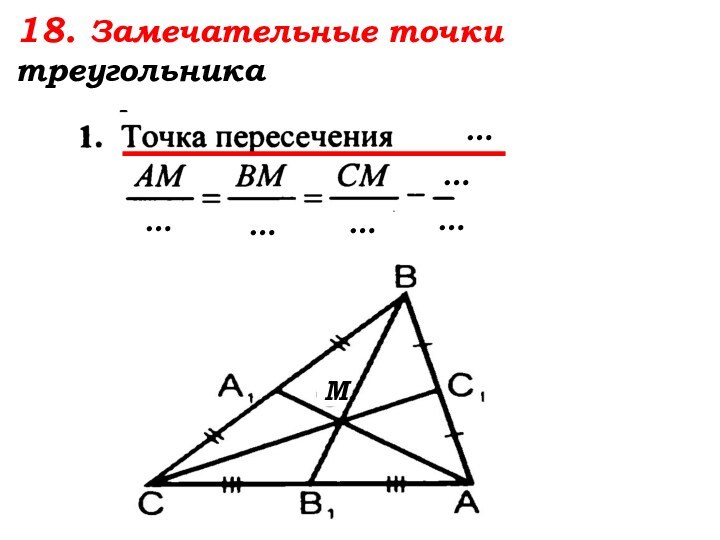
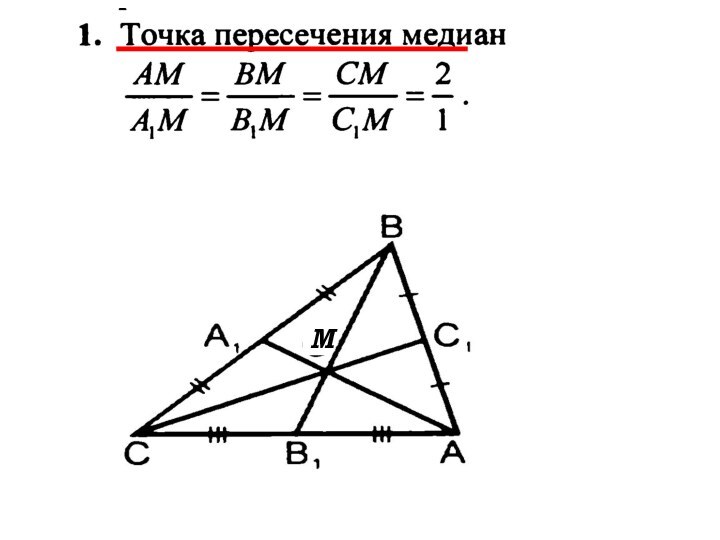
- 72. М…………18. Замечательные точки треугольника……
- 73. М
- 74. …………
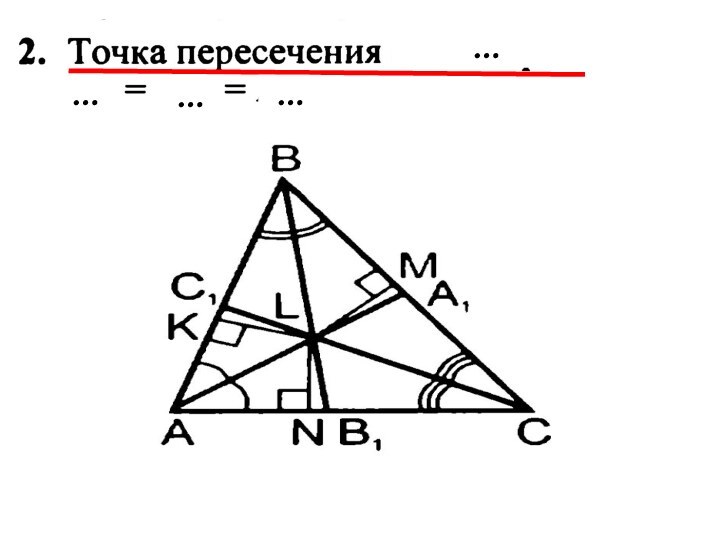
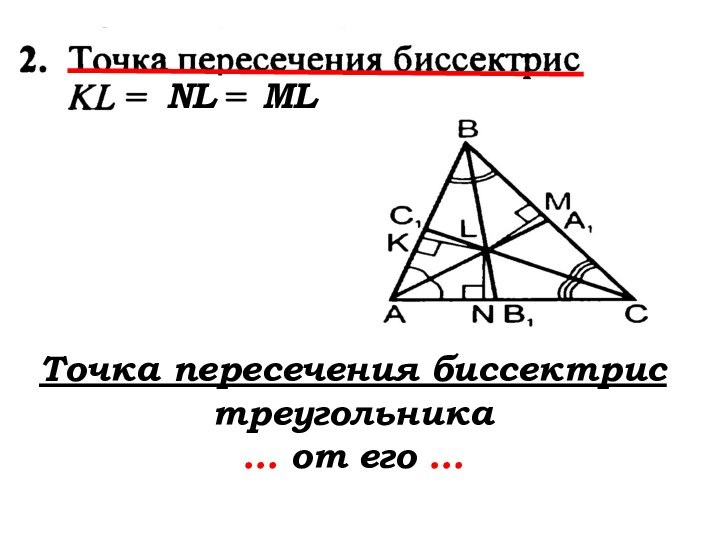
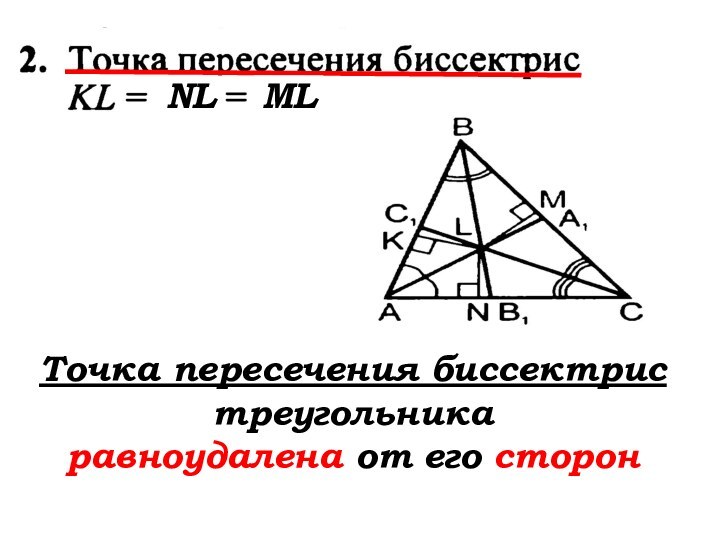
- 75. NLMLТочка пересечения биссектрис треугольника … от его …
- 76. NLMLТочка пересечения биссектрис треугольника равноудалена от его сторон
- 77. …………
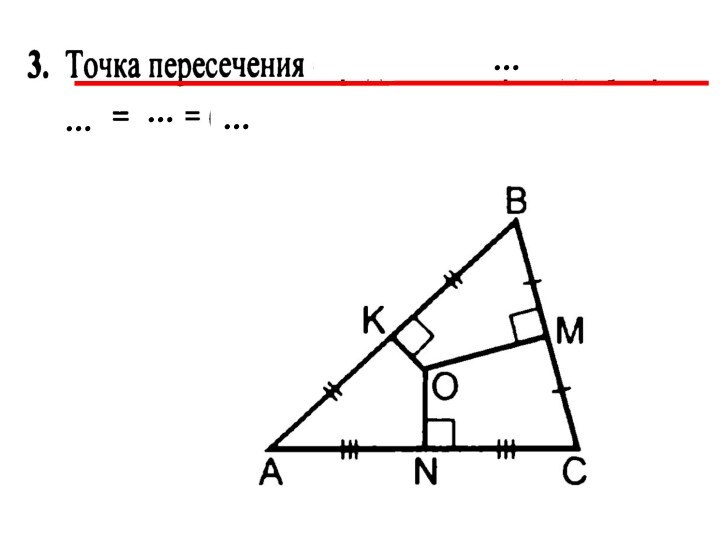
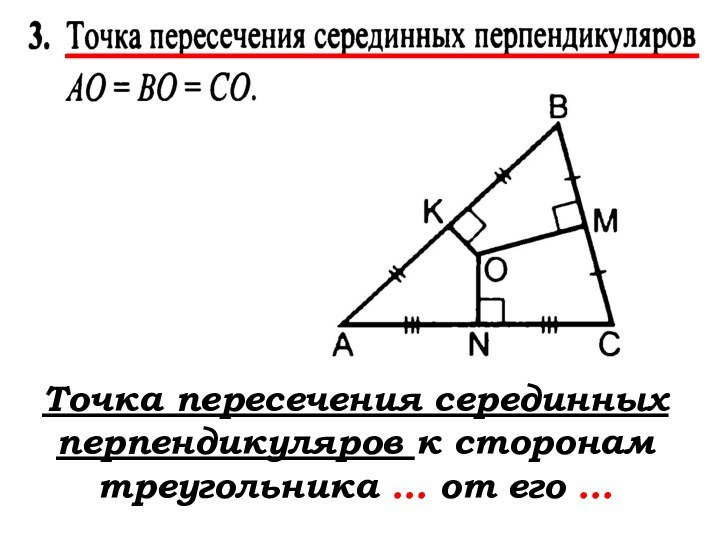
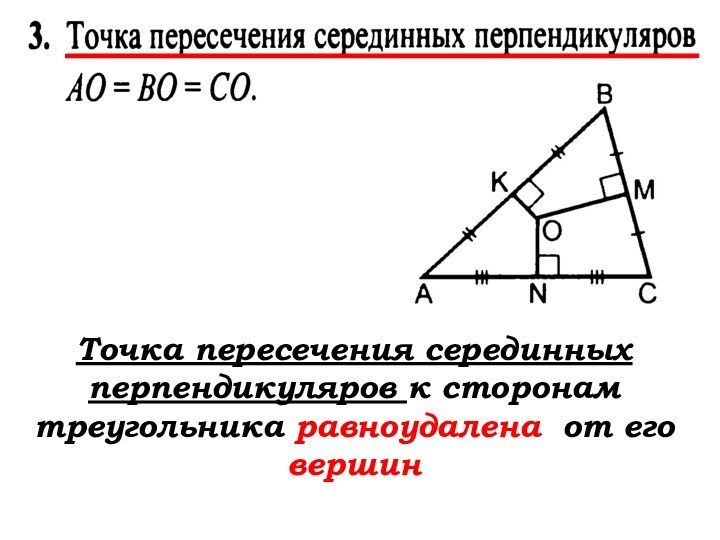
- 78. Точка пересечения серединных перпендикуляров к сторонам треугольника … от его …
- 79. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин
- 80. …
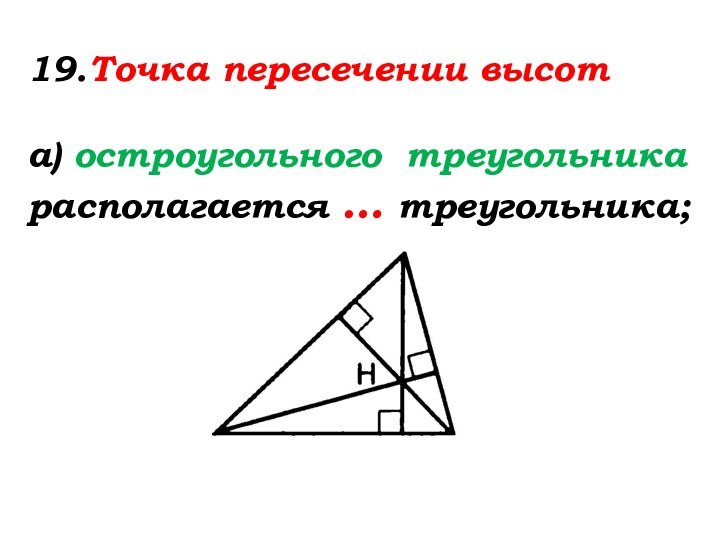
- 81. 19.Точка пересечении высота) остроугольного треугольникарасполагается … треугольника;
- 82. Точка пересечении высота) остроугольного треугольникарасполагается внутри треугольника;
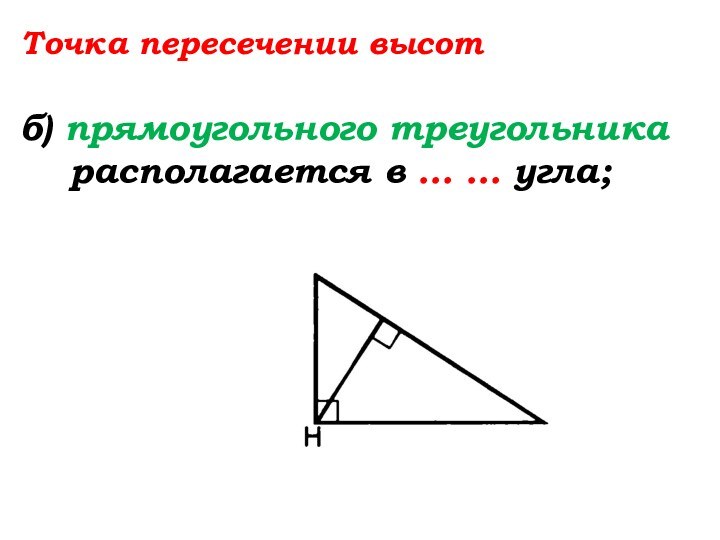
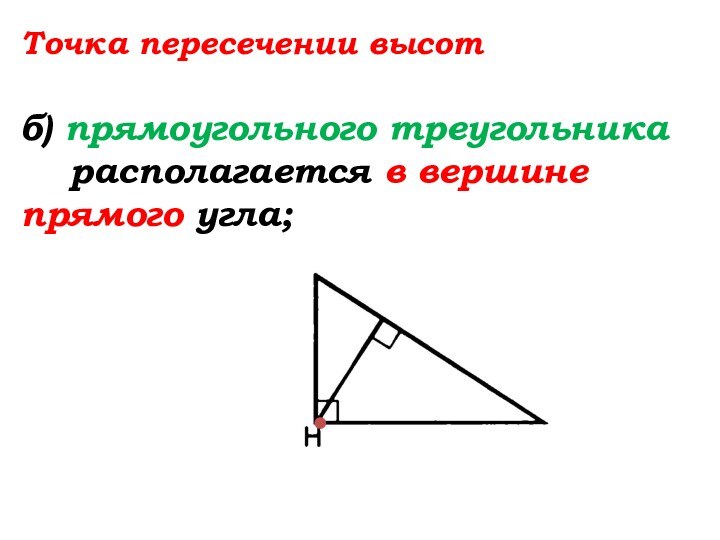
- 83. Точка пересечении высотб) прямоугольного треугольника располагается в … … угла;
- 84. Точка пересечении высотб) прямоугольного треугольника располагается в вершине прямого угла;
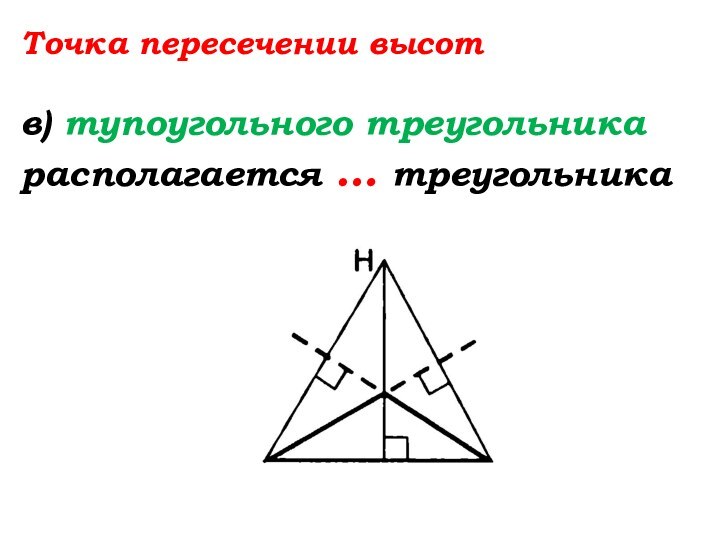
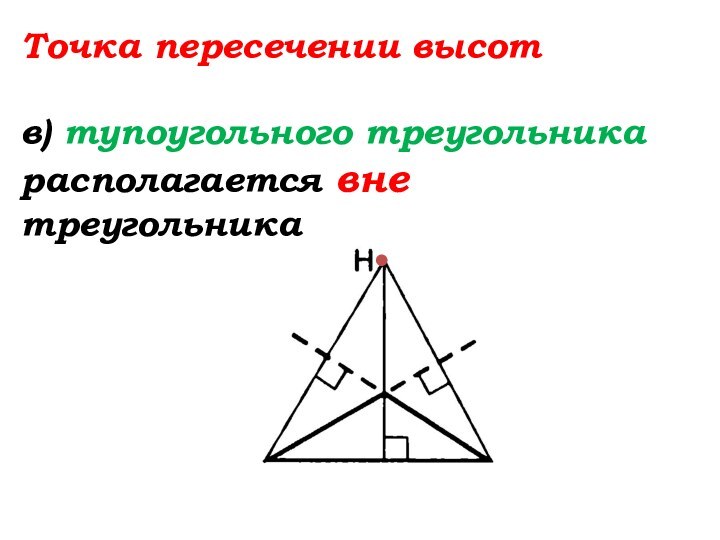
- 85. Точка пересечении высотв) тупоугольного треугольника располагается … треугольника
- 86. Точка пересечении высотв) тупоугольного треугольника располагается вне треугольника
- 87. 20. Центр окружности, описанной около треугольника, находится
- 88. 20. Центр окружности, описанной около треугольника, находится
- 89. 22. Центр окружности, описанной около-остроугольного треугольника находится
- 90. Центр окружности, описанной около-остроугольного треугольника находится
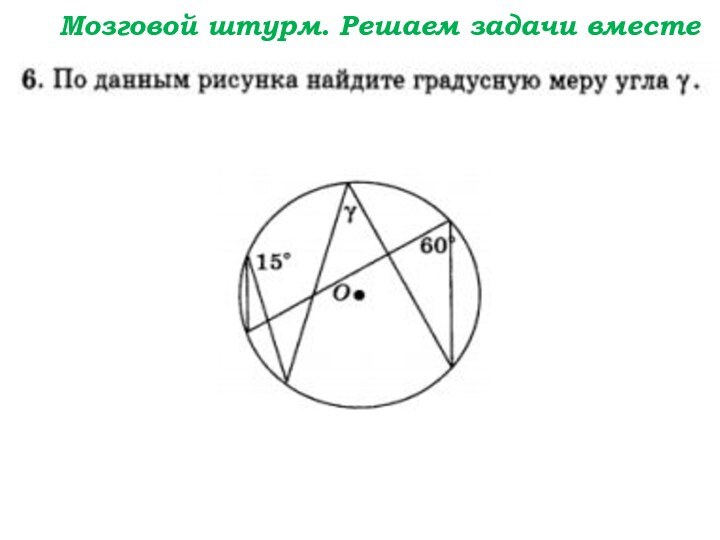
- 91. Мозговой штурм. Решаем задачи вместе
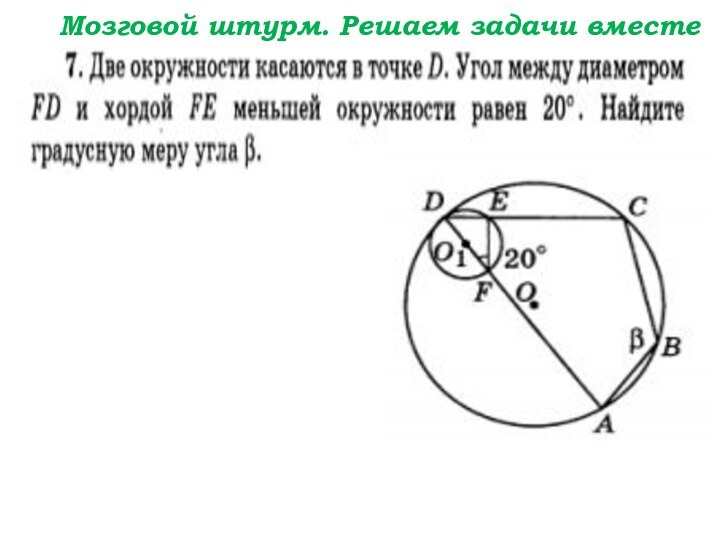
- 93. Мозговой штурм. Решаем задачи вместе
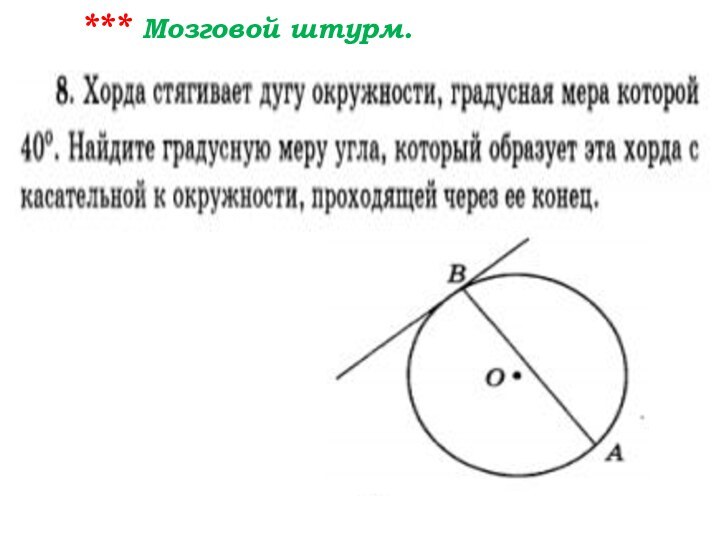
- 95. Мозговой штурм. Решаем задачи вместе
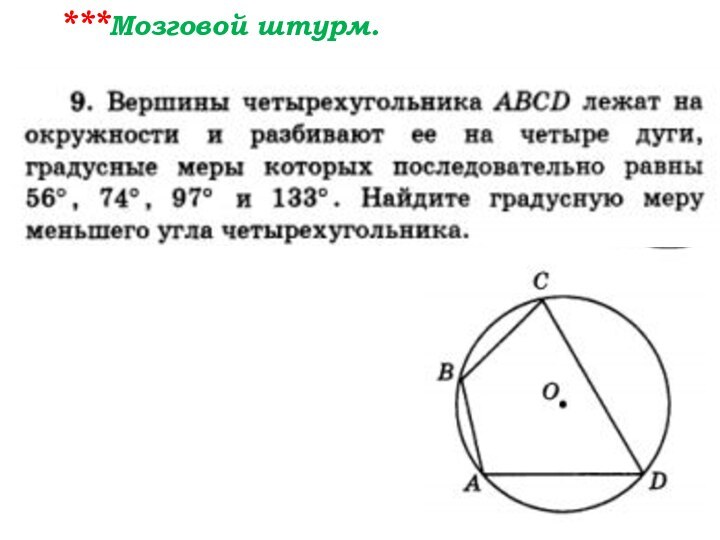
- 97. Мозговой штурм. Решаем задачи вместе
- 99. Мозговой штурм. Решаем задачи вместе
- 101. Мозговой штурм. Решаем задачи вместе
- 103. Мозговой штурм. Решаем задачи вместе
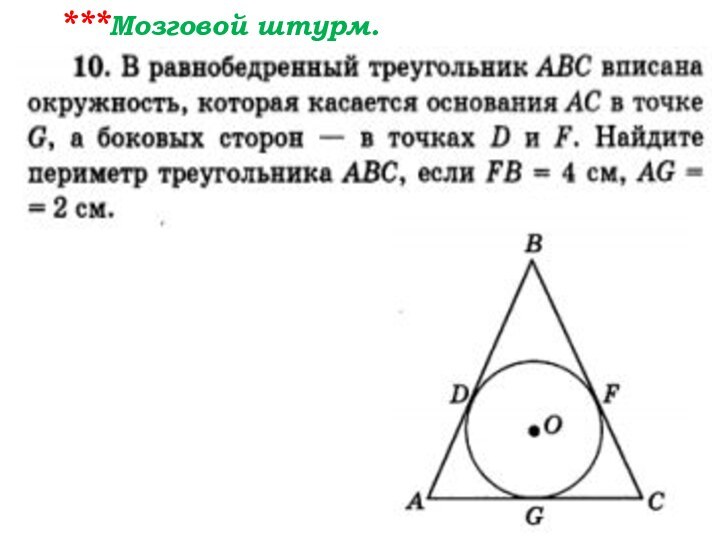
- 105. *** Мозговой штурм.
- 106. ***Мозговой штурм.
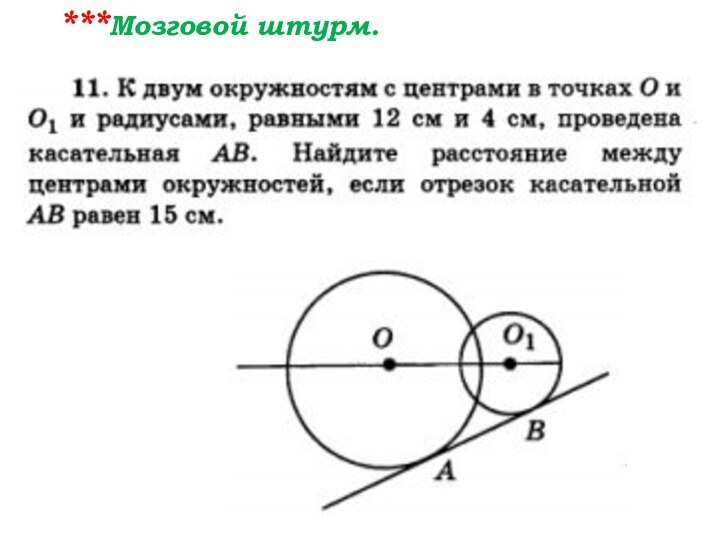
- 107. ***Мозговой штурм.
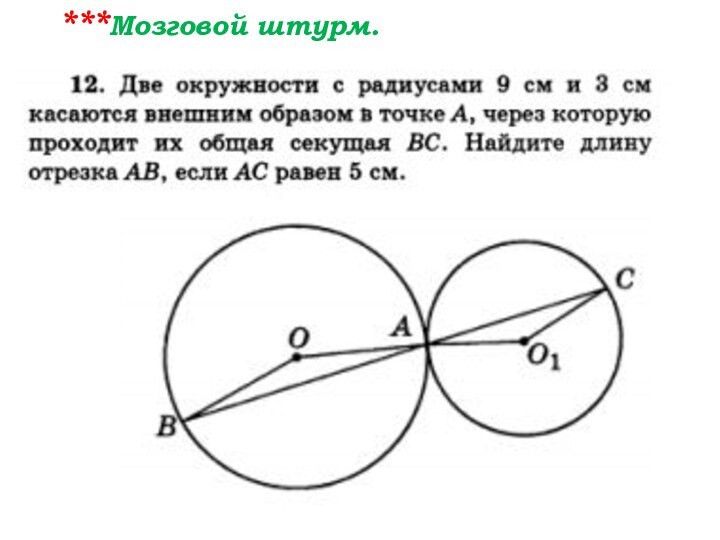
- 108. ***Мозговой штурм.
- 109. ***Мозговой штурм.
- 111. Назовите
- 112. 1.Теория. Повторить
- 113. Скачать презентацию
- 114. Похожие презентации
Приветствую вас на уроке геометрииУроки №1-207.09.17г.













































Слайд 5
Цели урока:
Повторить все виды углов и отрезков в
окружности.
Решать задачи по теме урока, используя теоремы и
формулы.Продолжить формирование культуры устной и письменной математической речи и культуры общения, умения работать в паре и группе.
Слайд 7
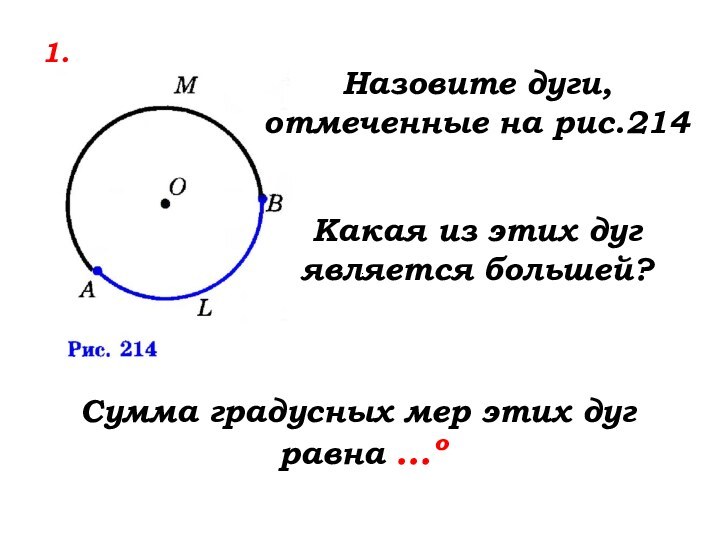
Назовите дуги, отмеченные на рис.214
Какая из этих дуг
является большей?
Сумма градусных мер этих дуг
равна …º
1.
Слайд 9
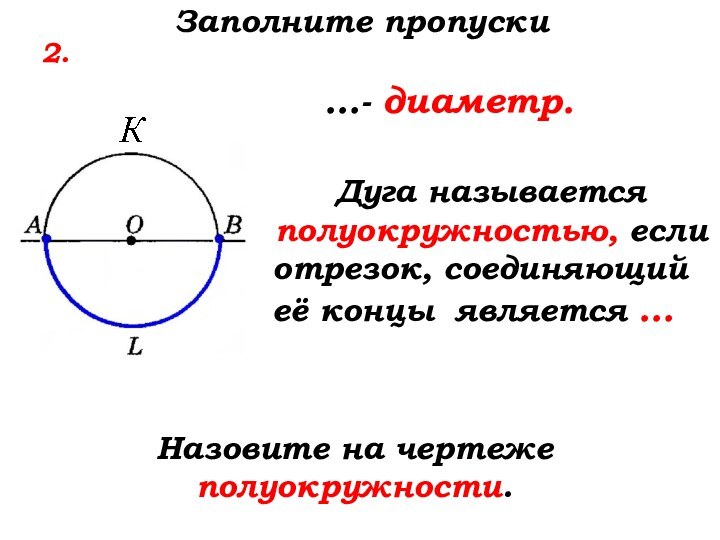
Дуга называется полуокружностью, если
отрезок, соединяющий её концы является
…
Назовите на чертеже полуокружности.
…- диаметр.
Заполните пропуски
2.
Слайд 10
Дуга называется полуокружностью, если
отрезок, соединяющий её концы является
диаметром
– полуокружности.
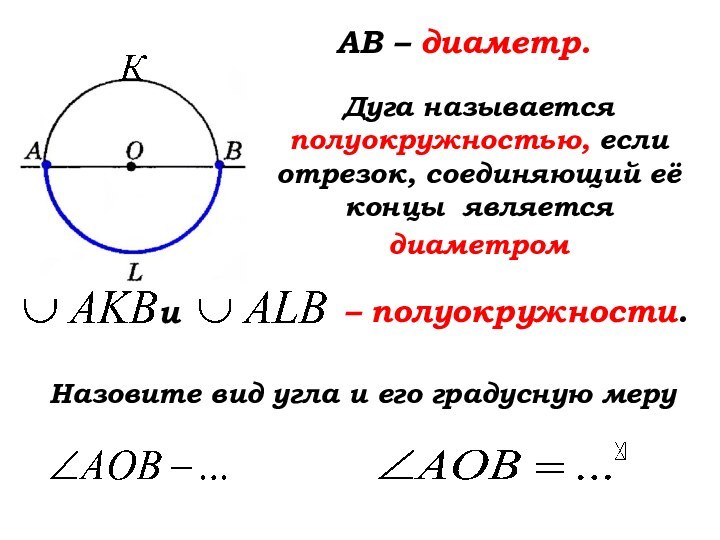
АВ – диаметр.
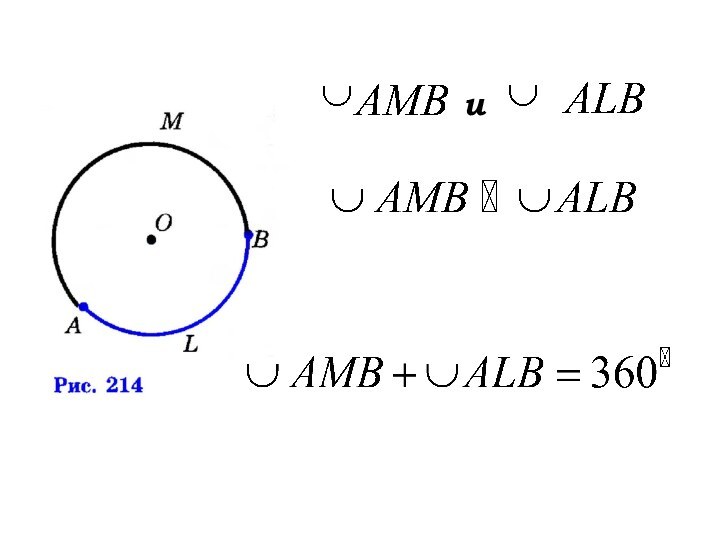
и
Назовите вид угла и его
градусную меру
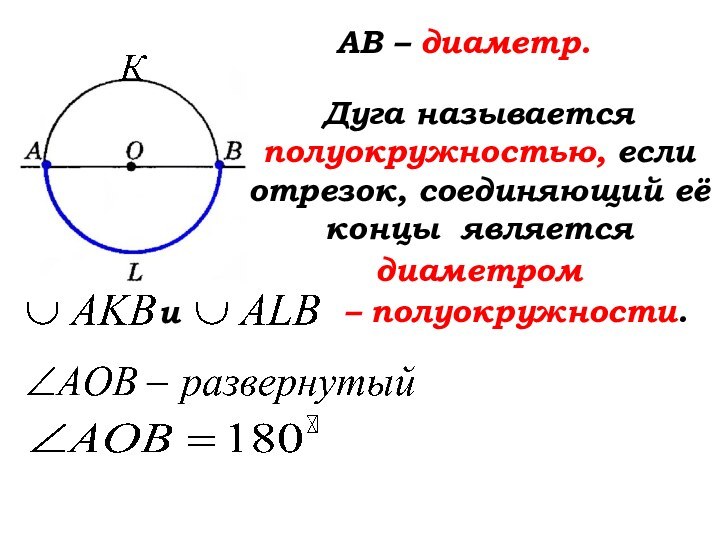
Слайд 11
Дуга называется полуокружностью, если
отрезок, соединяющий её концы является
диаметром
– полуокружности.
АВ – диаметр.
и
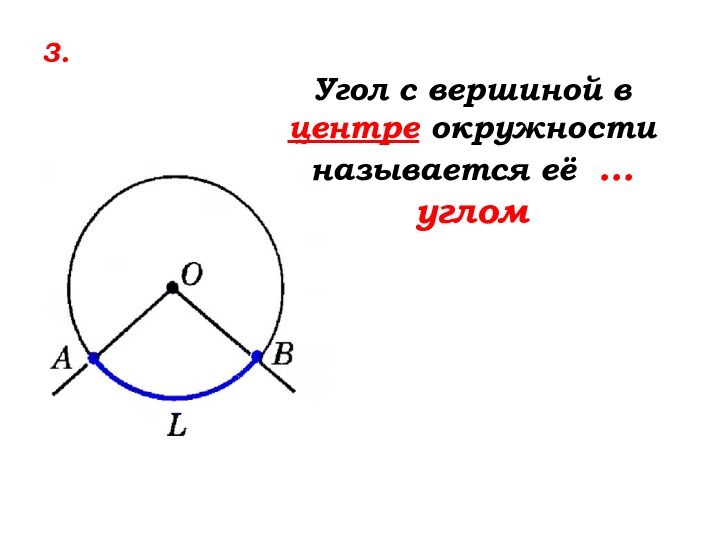
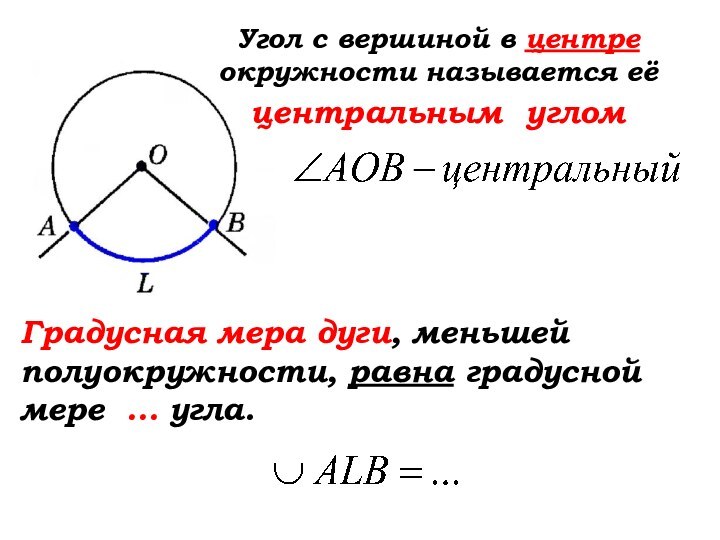
Слайд 14 Угол с вершиной в центре окружности называется её
центральным углом
Градусная мера дуги, меньшей полуокружности, равна градусной мере
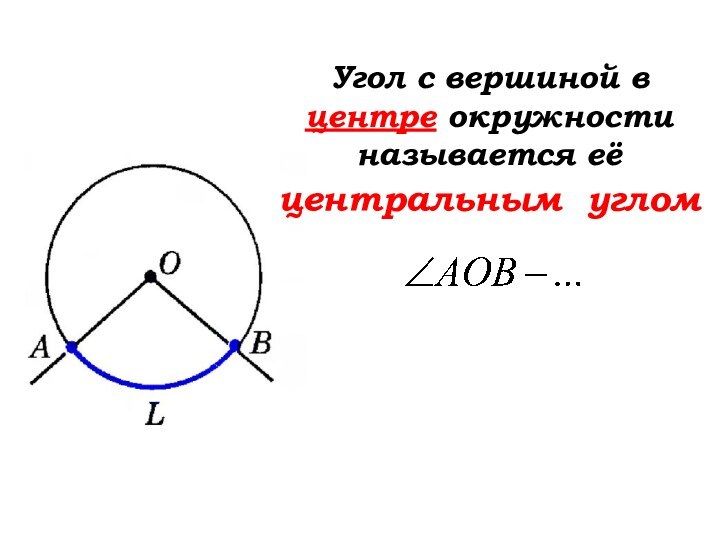
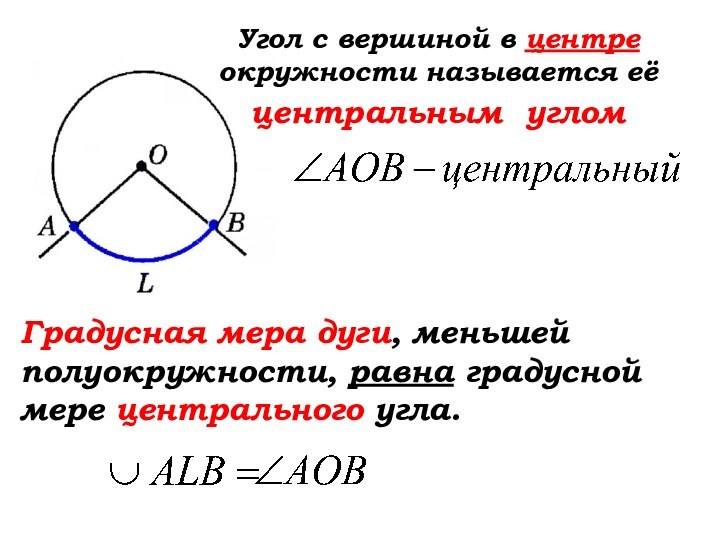
… угла. Слайд 15 Угол с вершиной в центре окружности называется её
центральным углом
Градусная мера дуги, меньшей полуокружности, равна градусной мере
центрального угла.
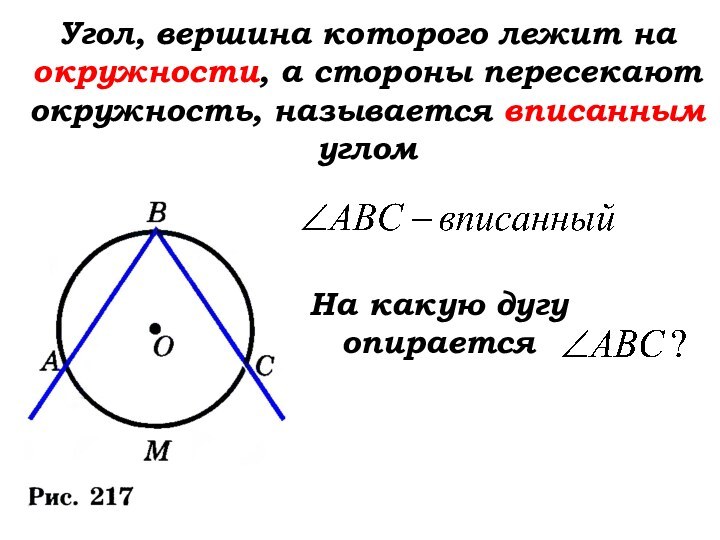
Слайд 19
Угол, вершина которого лежит на окружности, а
стороны пересекают окружность, называется вписанным углом
На какую дугу
опирается
Слайд 23
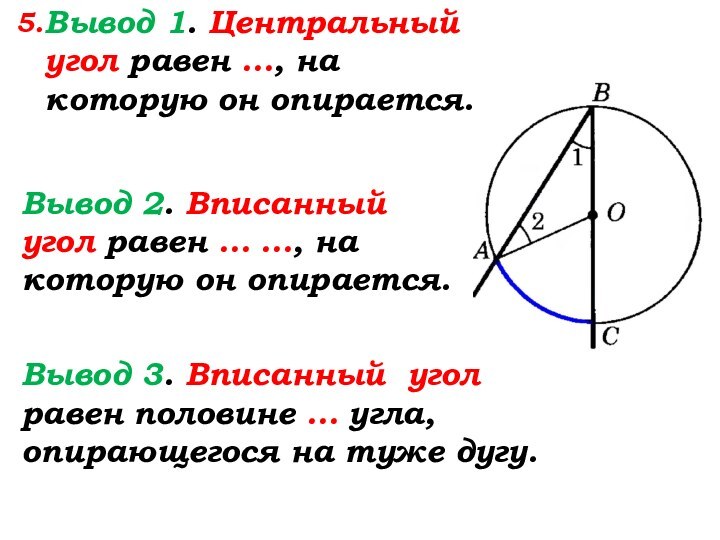
Вывод 1. Центральный угол равен …, на
которую он опирается.
Вывод 2. Вписанный угол равен … …,
на которую он опирается.Вывод 3. Вписанный угол равен половине … угла, опирающегося на туже дугу.
5.
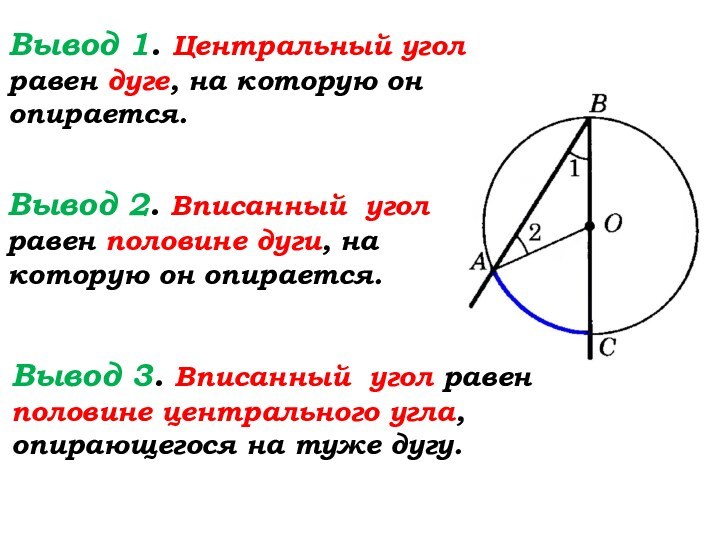
Слайд 24
Вывод 1. Центральный угол
равен дуге, на которую он опирается.
Вывод 2. Вписанный угол
равен половине дуги, на которую он опирается.Вывод 3. Вписанный угол равен половине центрального угла, опирающегося на туже дугу.
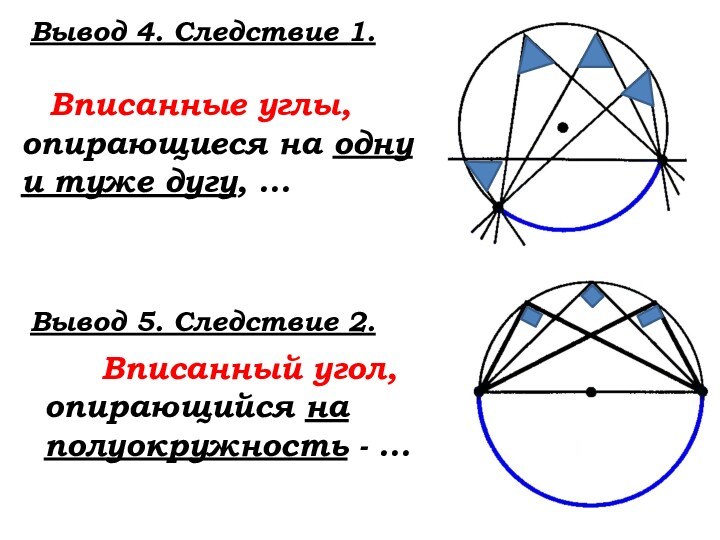
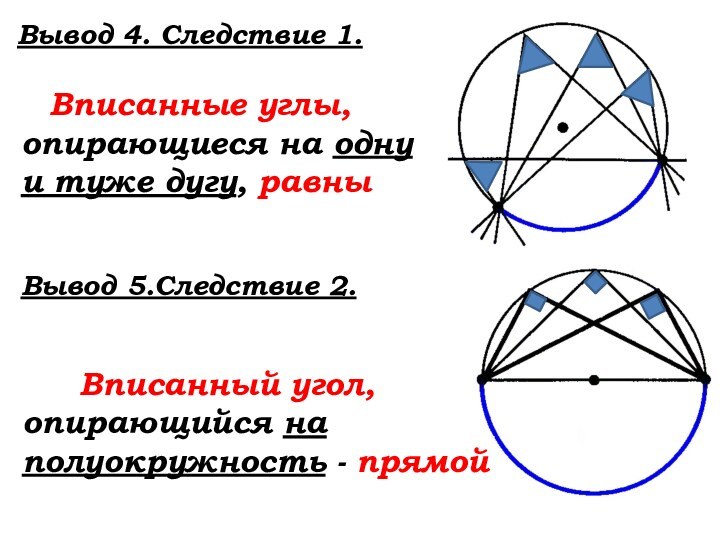
Слайд 25
Вывод 4. Следствие 1.
Вписанные углы,
опирающиеся на одну и туже дугу, …
Вывод 5. Следствие
2. Вписанный угол, опирающийся на полуокружность - …
Слайд 26
Вывод 4. Следствие 1.
Вписанные углы,
опирающиеся на одну и туже дугу, равны
Вывод 5.Следствие 2.
Вписанный угол, опирающийся на полуокружность - прямой
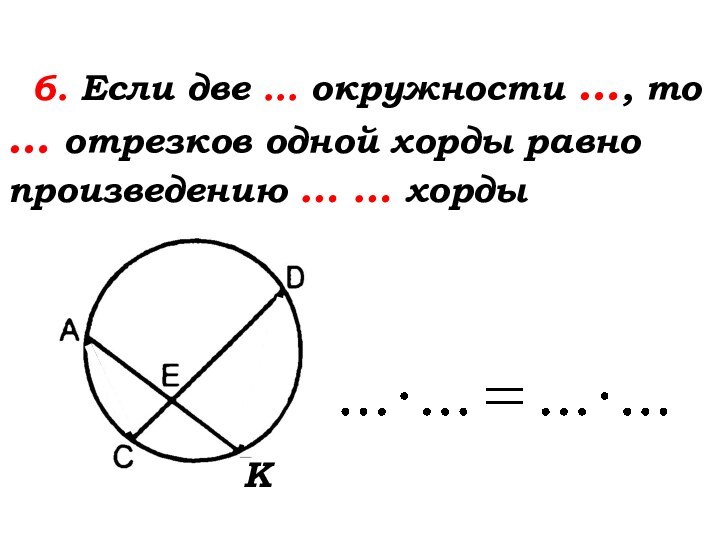
Слайд 28
6. Если две
хорды окружности пересекаются, то произведение отрезков одной хорды равно
произведению отрезков другой хордыК
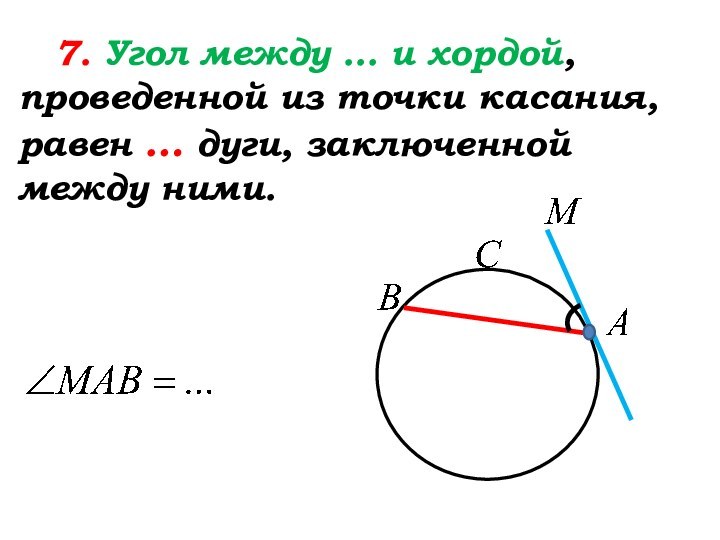
Слайд 29
7. Угол между … и
хордой, проведенной из точки касания, равен … дуги, заключенной
между ними.
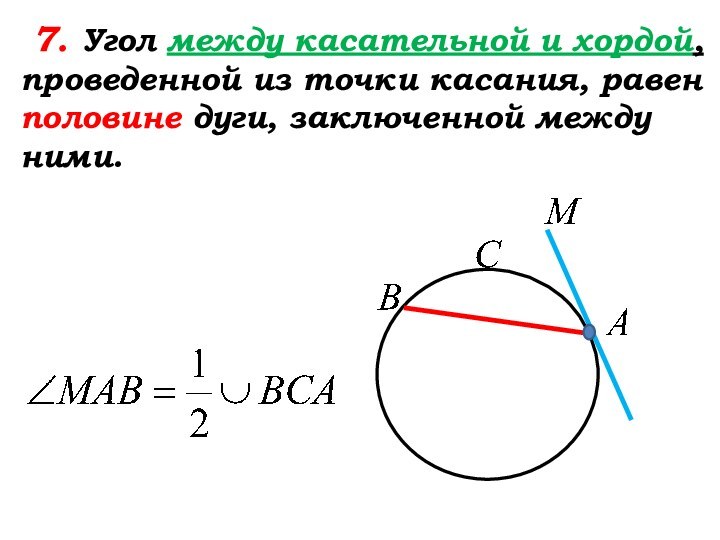
Слайд 30
7. Угол между касательной и хордой,
проведенной из точки касания, равен половине дуги, заключенной между
ними.
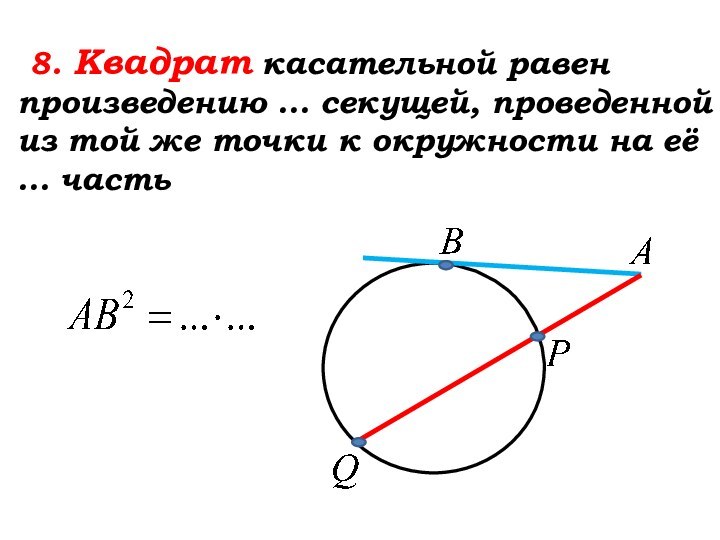
Слайд 31
8. Квадрат касательной равен произведению …
секущей, проведенной из той же точки к окружности на
её … часть
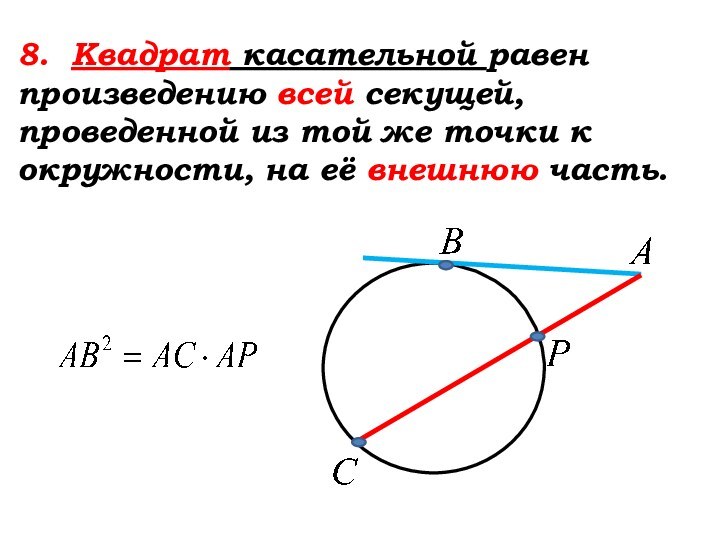
Слайд 32
8. Квадрат касательной равен произведению всей секущей,
проведенной из той же точки к окружности, на её
внешнюю часть.
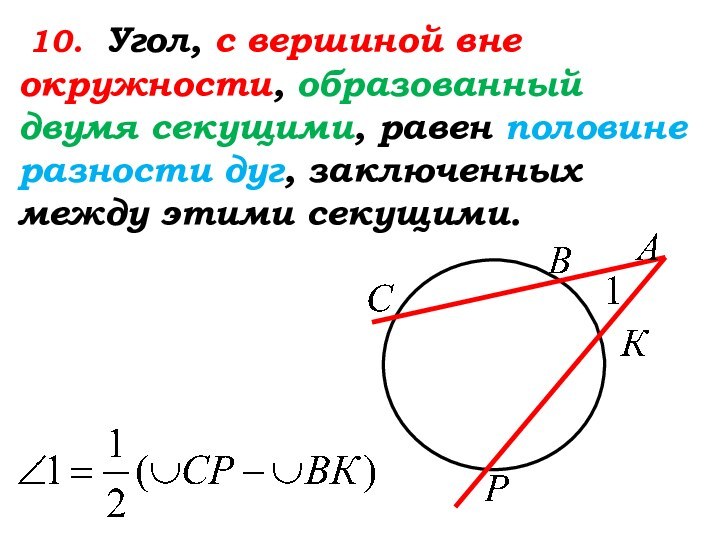
Слайд 35
10. Угол, с вершиной вне окружности,
образованный … …, равен … разности дуг, заключенных между
этими секущими.
Слайд 36
10. Угол, с вершиной вне окружности,
образованный двумя секущими, равен половине разности дуг, заключенных между
этими секущими.
Слайд 37
11. Если угол образован … … хордами,
то он равен половине суммы дуг, заключенных между этими
хордами
Слайд 38
11. Если угол образован двумя пересекающимися хордами,
то он равен половине суммы дуг, заключенных между этими
хордами
Слайд 39
Решение
задач письменно
на использование рассмотренного материала:
Разбор задачи
Решение задачи в
пареОбсуждение решения
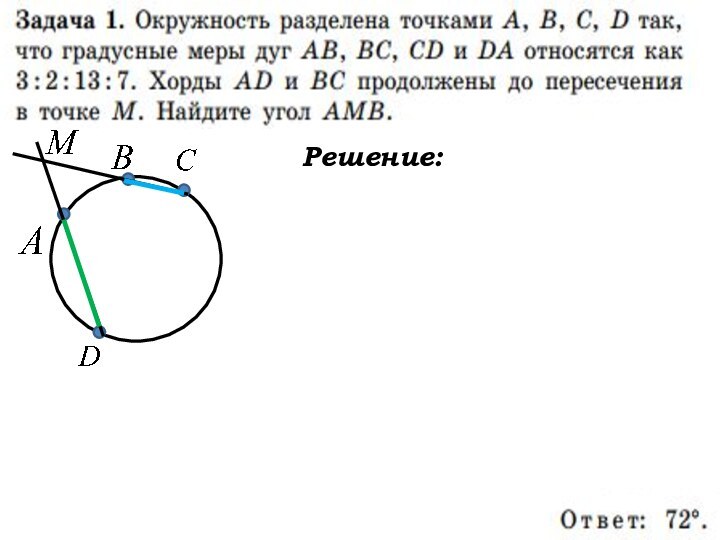
Слайд 40
1. Прочитайте задачу. Выполните чертёж окружности.
2.
Отметьте данные точки.
3. Проведите хорды.
4. Рассмотрите угол
АМВ, как угол, образованный … (предложите вариант решения)
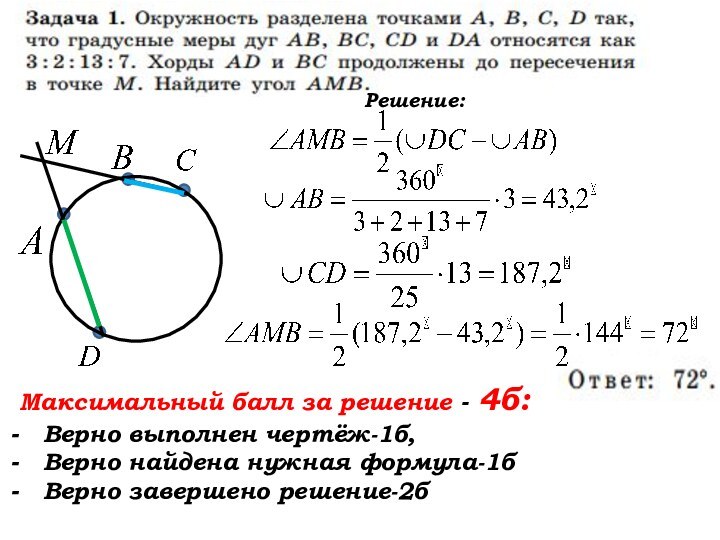
Слайд 43
Решение:
Максимальный балл за решение - 4б:
Верно
выполнен чертёж-1б,
Верно найдена нужная формула-1б
Верно завершено решение-2б
Слайд 44
1. Выполните чертёж окружности.
2. Отметьте точки.
3. Проведите необходимые по условию отрезки.
4. …
Слайд 45
1. Выполните чертёж окружности.
2. Отметьте точки.
3. Проведите необходимые по условию отрезки.
4. Познакомьтесь с
указанием 5. Решите задачу - докажите требуемое
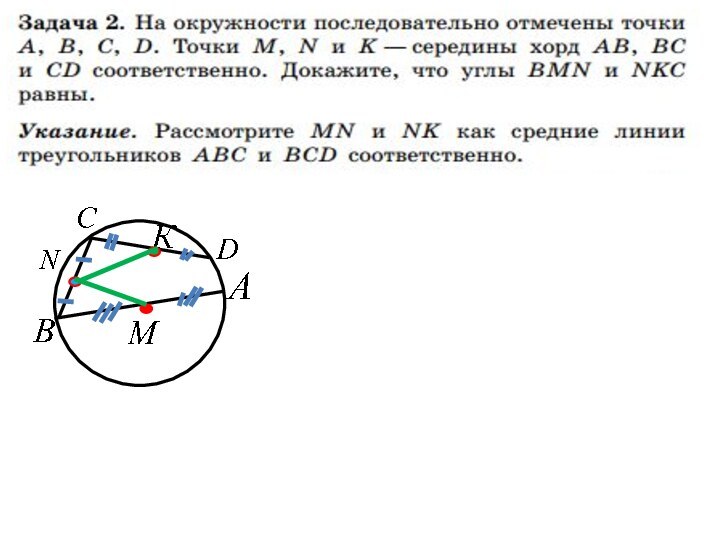
Слайд 47
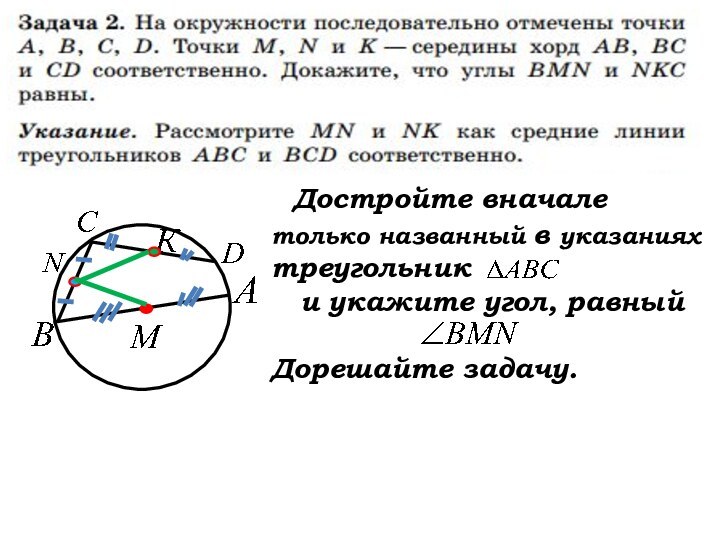
Достройте вначале только названный в указаниях треугольник
и укажите угол, равный
Дорешайте задачу.
Слайд 48
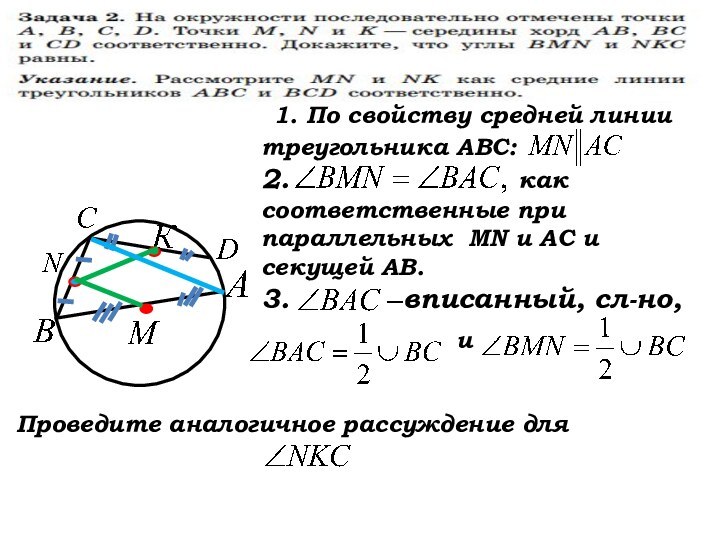
1. По свойству средней линии треугольника АВС:
2.
как соответственные при параллельных MN и АС и секущей АВ.
3. вписанный, сл-но,
Проведите аналогичное рассуждение для
и
Слайд 49
Максимальный балл за решение - 4б:
Верно выполнялись
чертёжи-1б,
Верно использовались свойства-1б
Верно завершено решение-2б
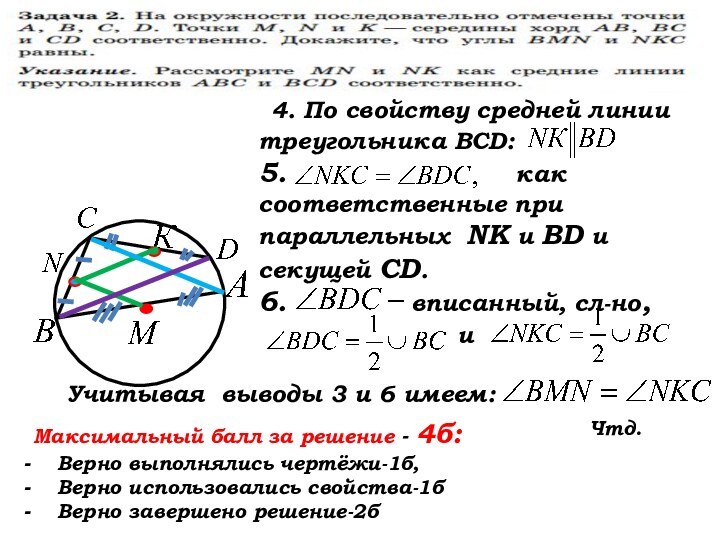
Учитывая выводы 3 и 6
имеем:Чтд.
4. По свойству средней линии треугольника ВСD:
5. как соответственные при параллельных NK и BD и секущей CD.
6. вписанный, сл-но,
и
Слайд 50
12.а)
Если расстояние от центра окружности до прямой меньше радиуса
окружности, то прямая и окружность имеют … … …и прямая называется …
Слайд 51
а)
Если расстояние от центра окружности до прямой меньше радиуса
окружности, то прямая и окружность имеют две общие точкии прямая называется секущей
Слайд 52
б) Если расстояние от
центра окружности до прямой больше радиуса окружности, то прямая
и окружность …имеют … …
Слайд 53
б) Если расстояние от
центра окружности до прямой больше радиуса окружности, то прямая
и окружность не имеют общих точек
Слайд 54
в)
Если расстояние от центра окружности до прямой равно радиусу
окружности, то прямая и окружность имеют … … … …, и прямая называется …
Слайд 55
в)
Если расстояние от центра окружности до прямой равно радиусу
окружности, то прямая и окружность имеют ровно одну общую точку, и прямая называется касательной к окружности
Слайд 58
б)
Если прямая, проходит через конец радиуса, … на окружности
и … к этому радиусу, то она является… … … …
Слайд 59
б)
Если прямая, проходит через конец радиуса, лежащий на окружности
и перпендикулярна к этому радиусу, то она является касательной к этой окружности
Слайд 60
14. Отрезки
касательных, проведенных к окружности из одной точки … и
составляют с … углы с прямой, проходящей через эту … и … окружности
Слайд 61
Отрезки
касательных, проведенных к окружности из одной точки равны и
составляют равные углы с прямой, проходящей через эту точку и центр окружности
Слайд 64
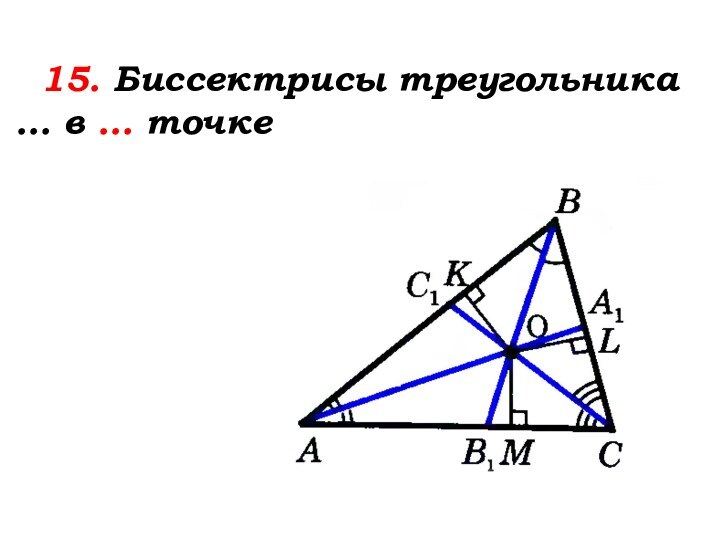
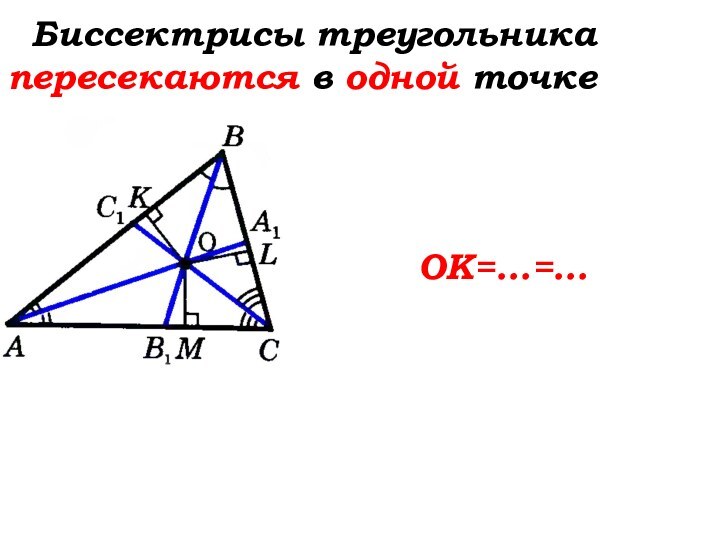
Биссектрисы треугольника пересекаются в одной
точке
OK=OL=OM
Точка пересечения биссектрис треугольника … от его …
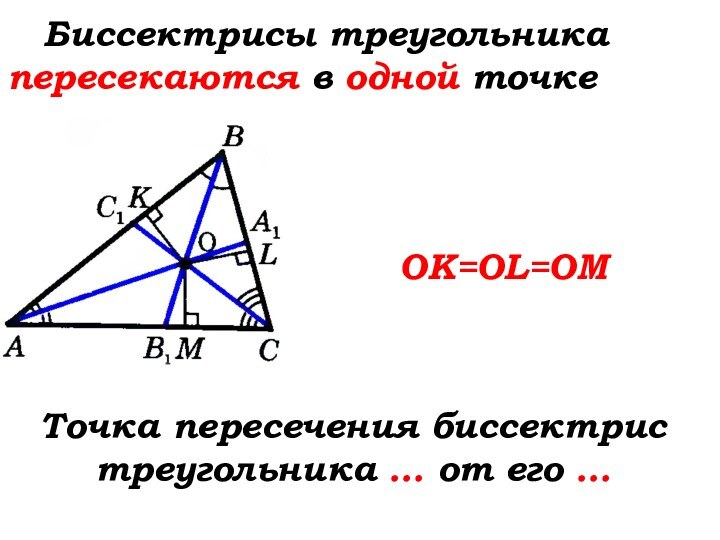
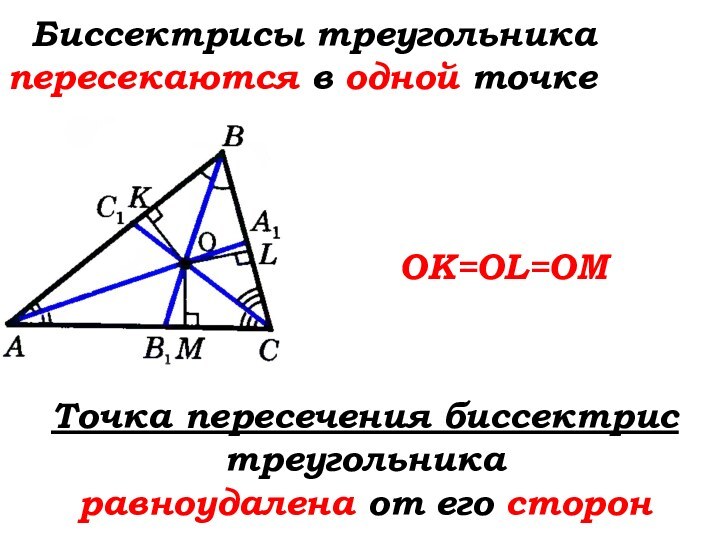
Слайд 65
Биссектрисы треугольника пересекаются в одной точке
OK=OL=OM
Точка
пересечения биссектрис треугольника
равноудалена от его сторон
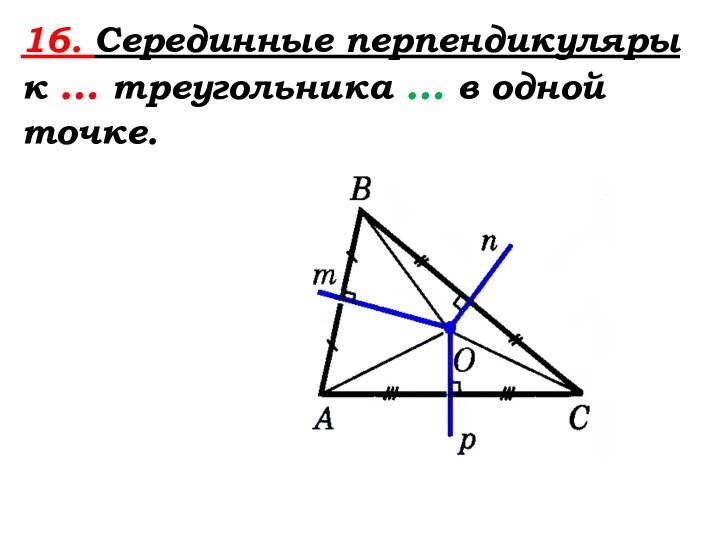
Слайд 67
Серединные перпендикуляры к сторонам треугольника пересекаются в
одной точке.
Какими являются отрезки
OА,OВ,OС?
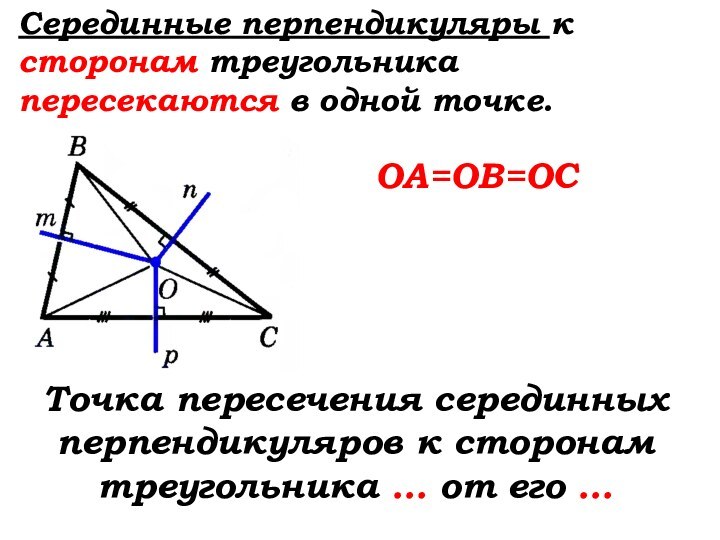
Слайд 68
Серединные перпендикуляры к сторонам треугольника пересекаются в
одной точке.
OА=OВ=OС
Точка пересечения серединных перпендикуляров к сторонам треугольника …
от его …
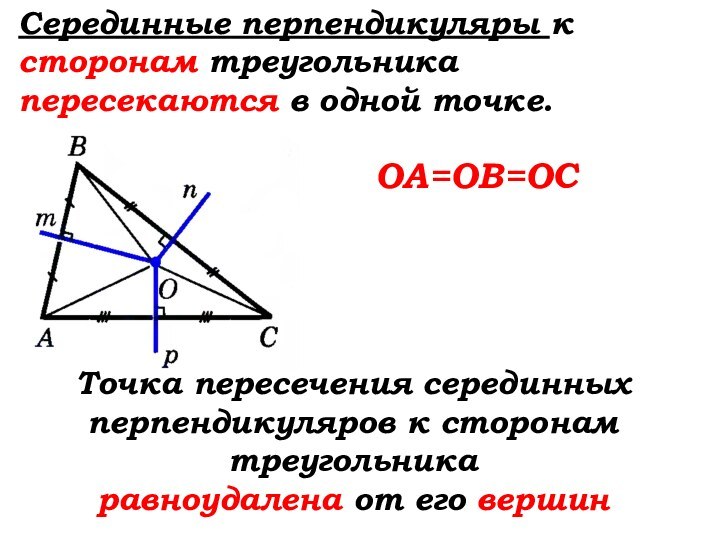
Слайд 69
Серединные перпендикуляры к сторонам треугольника пересекаются в
одной точке.
OА=OВ=OС
Точка пересечения серединных перпендикуляров к сторонам треугольника
равноудалена
от его вершин
Слайд 79
Точка пересечения серединных перпендикуляров к сторонам треугольника
равноудалена от его вершин
Слайд 84
Точка пересечении высот
б) прямоугольного треугольника
располагается в вершине прямого угла;
Слайд 87
20. Центр окружности,
описанной около треугольника, находится в
точке пересечения…
21. Центр окружности,
вписанной в треугольник, находится в
точке пересечения…
Слайд 88
20. Центр окружности,
описанной около треугольника, находится в
точке пересечения серединных перпендикуляров
21. Центр окружности,
вписанной в треугольник,
находится в точке пересечения биссектрис
Слайд 89
22. Центр окружности,
описанной около
-остроугольного треугольника находится …
…;
-прямоугольного треугольника находится … …;
-тупоугольного треугольника находится … …
Слайд 90
Центр окружности,
описанной около
-остроугольного треугольника находится внутри
треугольника;
-прямоугольного треугольника находится в середине гипотенузы;
-тупоугольного треугольника находится вне
треугольника
Слайд 112
1.Теория. Повторить теорию
(если есть необходимость выучить заново).
Разобрать задачи, решенные в
классе.2.Практика. Решить задачи: №№8 – 12
(из КР)
Выполнить тест.
ДР№1 на 14.09.17
Тест