Презентация на тему по геометрии Теорема Пифагора (8 класс)

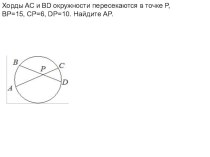
теореме Пифагора и о различных способах её доказательства. Причина

такой популярности теоремы: это простота, красота и широкая значимость.

Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков.

теоремы Пифагора. Всего известно около 500 различных доказательств теоремы

Пифагора.
Большинство способов её доказательства сводятся к разбиению квадратов на более мелкие части. Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов.

н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик

по драгоценным камням. Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Многие, имея на то основания, считали, что Пифагор – это не имя, а прозвище. Поскольку мудрый учитель высказывал истину столь же постоянно и авторитетно, как и дельфийская Пифия, он был прозван Пифагором.
Слово Пифагор можно перевести как «вещающий как Пифия». Версия о том, что Пифагор это имя не собственное, а прозвище, представляется наиболее правдоподобной.

учёному принесла доказанная им теорема, которая сейчас носит его

имя.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. (ок. 580 – ок. 500 г. до н.э.) Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками, ими было сделано много важных открытий в арифметике и геометрии. Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.

равен сумме квадратов катетов

«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме

площадей квадратов, построенных на его катетах». Действительно, с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах.

сумме квадратов, построенных на его катетах».
Простейшее доказательство теоремы получается

в случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. Достаточно посмотреть на получившиеся равнобедренные прямоугольные треугольники, чтобы убедиться в справедливости теоремы. Для равнобедренного треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 маленьких треугольника, а квадраты, построенные на катетах, - по 2.

получение равенства суммы площадей квадратов, построенных на катетах прямоугольного

треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали покрой мужских штанов, что породило шуточные стихотворения.

Пифагоровы штаны

Например: Пифагоровы штаны на все стороны равны.

BC²=AB²+AC². Построим отрезок CD равный отрезку AB на продолжении

катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E.

Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:

Фигура ABED является трапецией, значит, её площадь равна:

Если приравнять левые части найденных выражений, то получим:

После алгебраических преобразований получим:

бечёвку, разделённую узлами на 12 равных частей.

Покажите, как

они это делали.

Треугольник со сторонами 3, 4 и 5 называется египетским

к стене лестницу прибрати, стены же тоя высота есть

117 стоп. И обрете лестницу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.

рос тополь одинокий.
Вдруг ветра порыв его ствол надломал. Бедный

тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

цвет. Он рос одиноко. И ветер порывом Отнес его в сторону.

Нет Боле цветка над водой. Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода Здесь глубока?