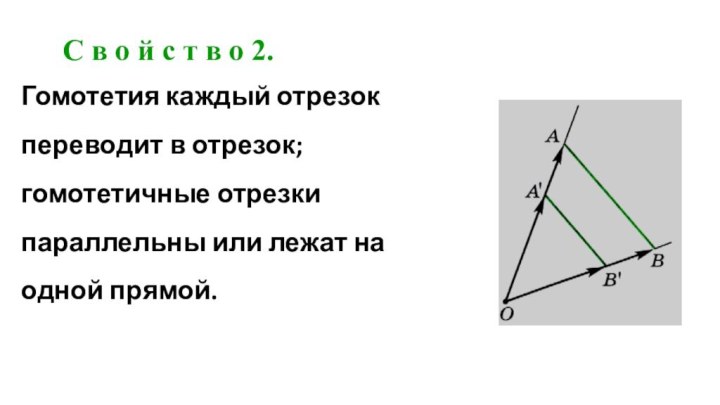
что, как мы покажем, любое подобие является композицией гомотетии
и движения. Поэтому, изучив свойства гомотетии и зная свойства движений, мы, сопоставив их, найдем свойства подобия.Рассмотрим важнейшие свойства гомотетии.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















Д о к а з а т е л ь с т в о: