- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку по теме пирамида 10 класс геометрия
Содержание
- 2. Домашнее задание:П.18, № 18.4;18.29
- 3. Париж.Новый вход в ЛуврСевастополь. Храм-пирамида
- 4. Пирамиды в растениях
- 5. Пирамиды Теотиуакана (Мексика)
- 6. Определения Евклид, пирамиду определяет как телесную фигуру,
- 7. А. М. Лежандр в 1794 году в
- 8. Цели урокаВвести понятие пирамиды, дать определение пирамиды
- 9. Пирамида
- 10. Высота проецируется 9В вершину основанияНа сторону основанияВо внутреннюю область основанияВо внешнюю область основания
- 11. Группа 1 10
- 12. Определение пирамидыМногогранник, основание которого n- угольник, а боковые грани – треугольники, имеющие общую вершину.
- 13. Группа 2 11
- 14. Классификация пирамид 12Пирамиды классифицируются по числу
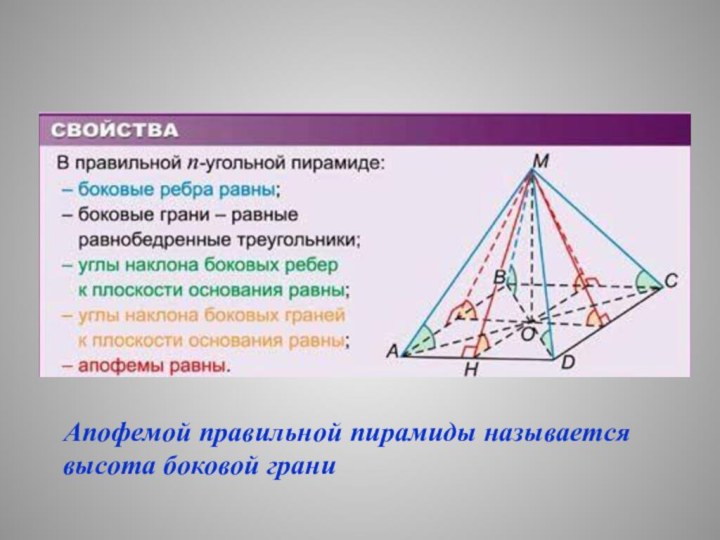
- 17. Определение правильной пирамиды
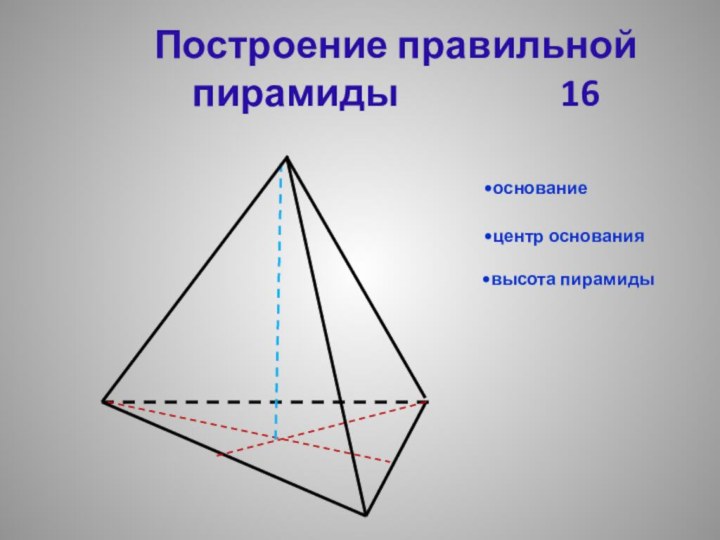
- 18. Построение правильной пирамиды 16высота пирамидыоснованиецентр основания
- 19. Апофема – высота боковой грани правильной пирамиды,
- 20. Апофемой правильной пирамиды называется высота боковой грани
- 21. Вывод формулы площади боковой поверхности пирамиды
- 22. Площадь боковой поверхности правильной пирамидыравна половине произведения периметра основания на апофему.
- 23. Площадь поверхности пирамиды
- 24. Пирамидой называется многогранник, который состоит из плоского
- 26. Все боковые ребра правильной пирамиды равны, а
- 27. Контрольные вопросы Продолжите предложения1) Высотой пирамиды
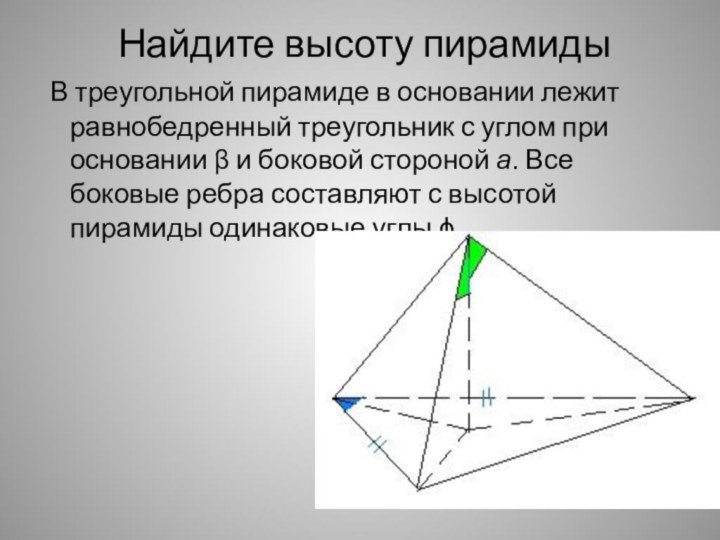
- 28. Найдите высоту пирамиды В треугольной пирамиде
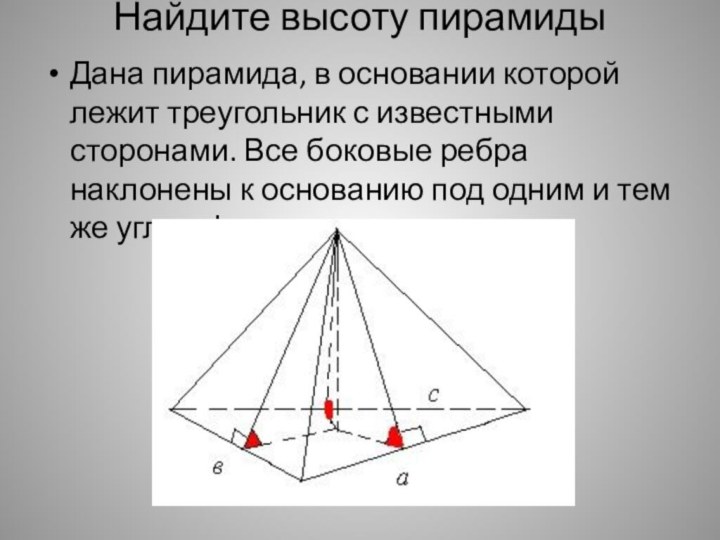
- 29. Найдите высоту пирамиды Дана пирамида,
- 30. Найдите высоту пирамидыДана пирамида, в основании
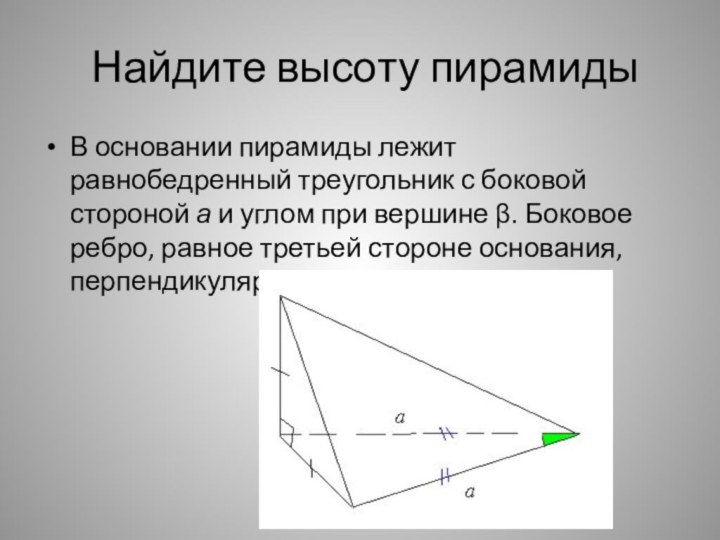
- 31. Найдите высоту пирамидыВ основании пирамиды лежит
- 32. Итог урокаПознакомились с понятием «пирамида», дали определение
- 33. Скачать презентацию
- 34. Похожие презентации
Домашнее задание:П.18, № 18.4;18.29
















Слайд 6
Определения
Евклид, пирамиду определяет как телесную фигуру, ограниченную
плоскостями, которые от каждой плоскости сходятся к одной точке.
Герон предложил следующее определение пирамиды: “Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник”.Слайд 7 А. М. Лежандр в 1794 году в своем
труде “Элементы геометрии” пирамиду определяет так: “Пирамида – телесная
фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”.
Слайд 8
Цели урока
Ввести понятие пирамиды, дать определение пирамиды
рассмотреть
виды пирамид
дать определение элементов пирамиды
вывести формулу нахождения
площади боковой и полной поверхностей пирамидыСлайд 9 Пирамида
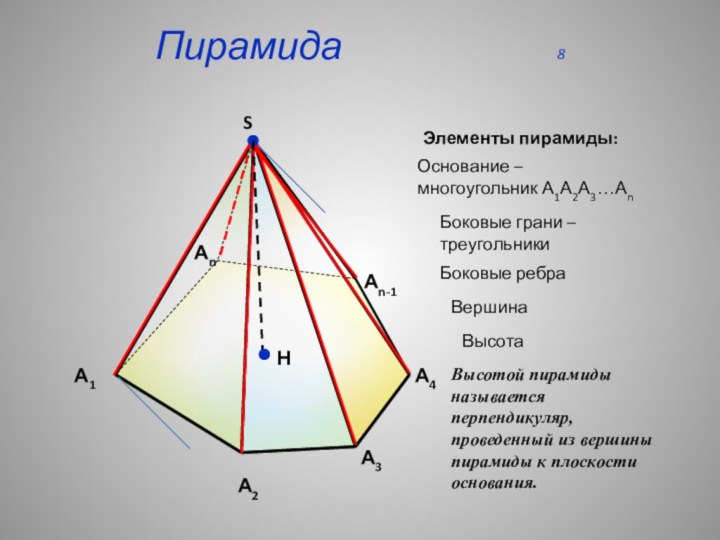
8
S
Элементы пирамиды:
Основание –
многоугольник А1А2А3…Аn
Боковые
грани – треугольники
Боковые ребра
Вершина
Высота
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Слайд 10
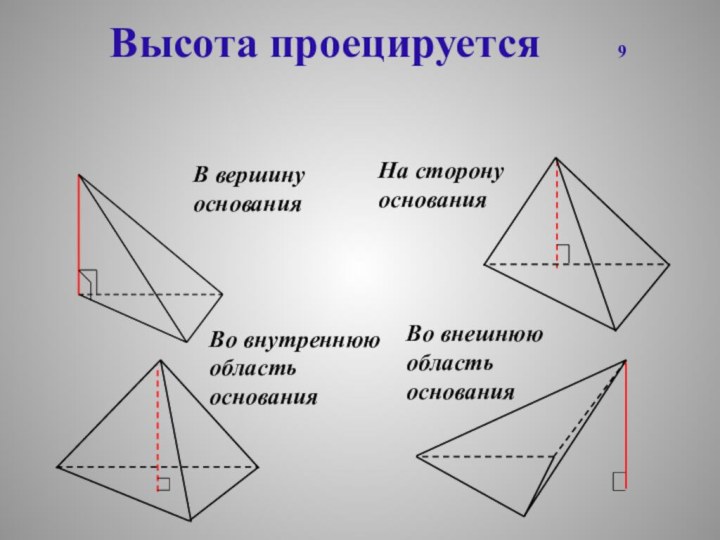
Высота проецируется 9
В вершину основания
На
сторону основания
Во внутреннюю область основания
Во внешнюю область основания
Слайд 12
Определение пирамиды
Многогранник, основание которого n- угольник, а боковые
грани – треугольники, имеющие общую вершину.
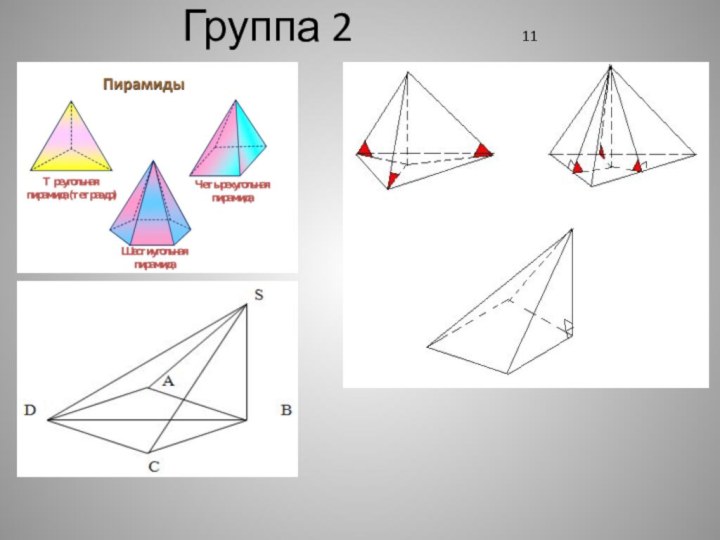
Слайд 14
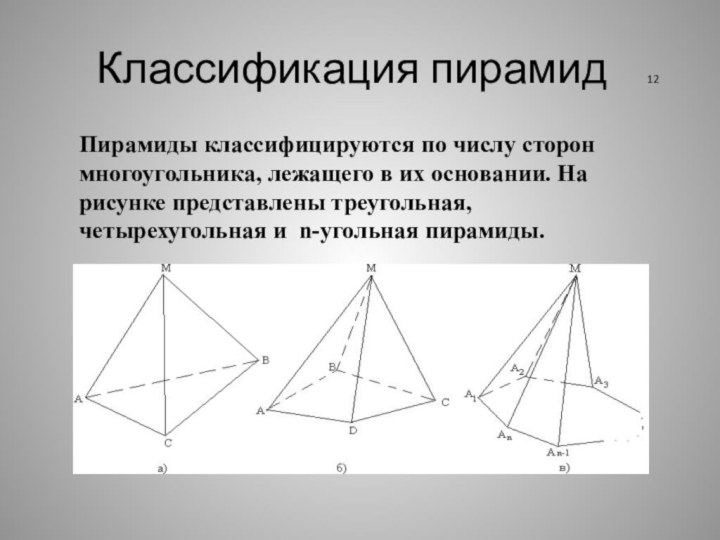
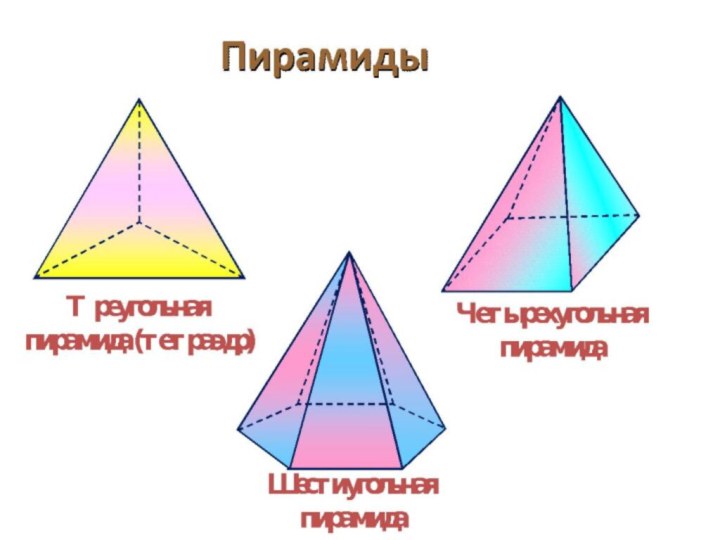
Классификация пирамид 12
Пирамиды классифицируются по числу сторон
многоугольника, лежащего в их основании. На рисунке представлены треугольная,
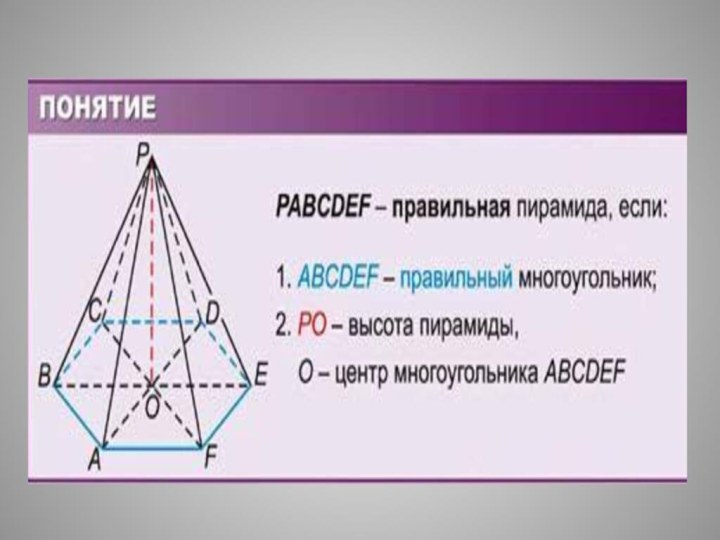
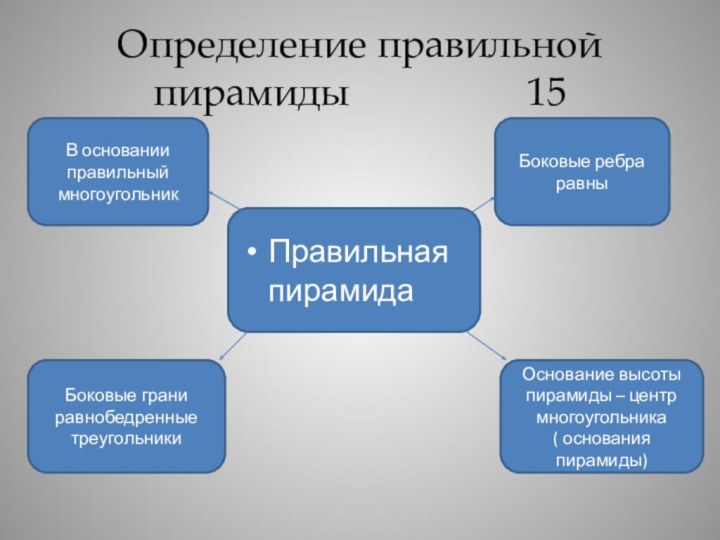
четырехугольная и n-угольная пирамиды.Слайд 17 Определение правильной пирамиды
15
Правильная пирамида
В основании правильный многоугольник
Боковые ребра
равныБоковые грани равнобедренные треугольники
Основание высоты пирамиды – центр многоугольника
( основания пирамиды)
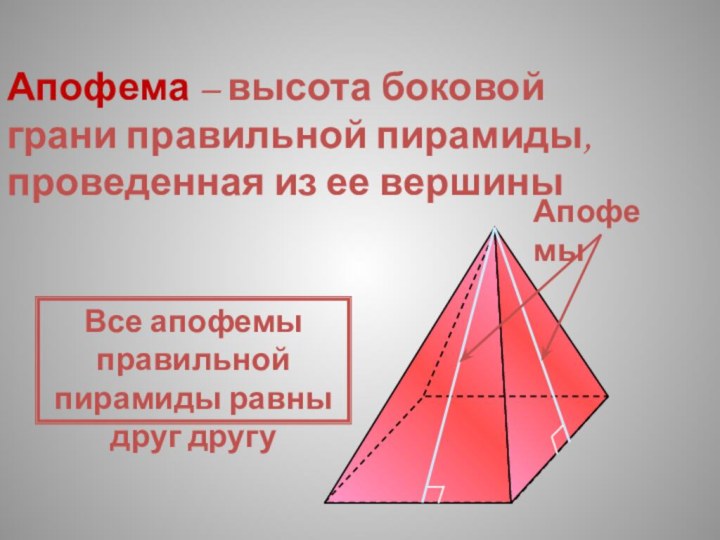
Слайд 19 Апофема – высота боковой грани правильной пирамиды, проведенная
из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг
другу
Слайд 22
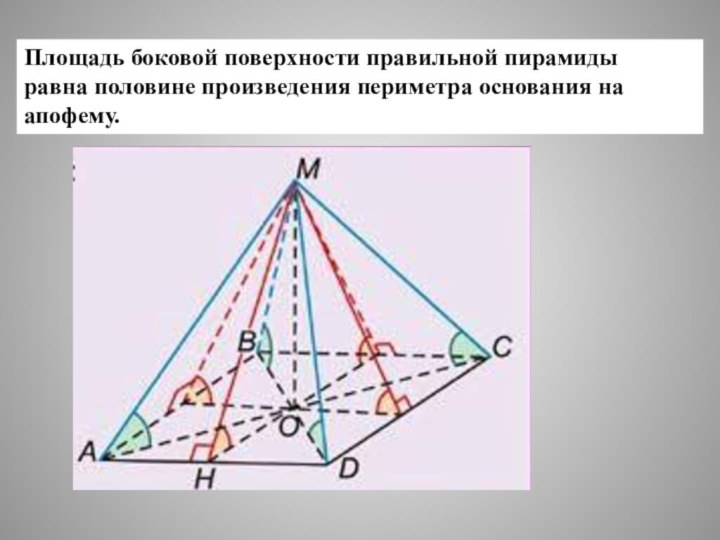
Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра
основания на апофему.
Слайд 23 Площадь поверхности пирамиды
21
Sпол = Sбок + Sосн
Площадь боковой поверхности –
сумма
площадей боковых граней (треугольников)
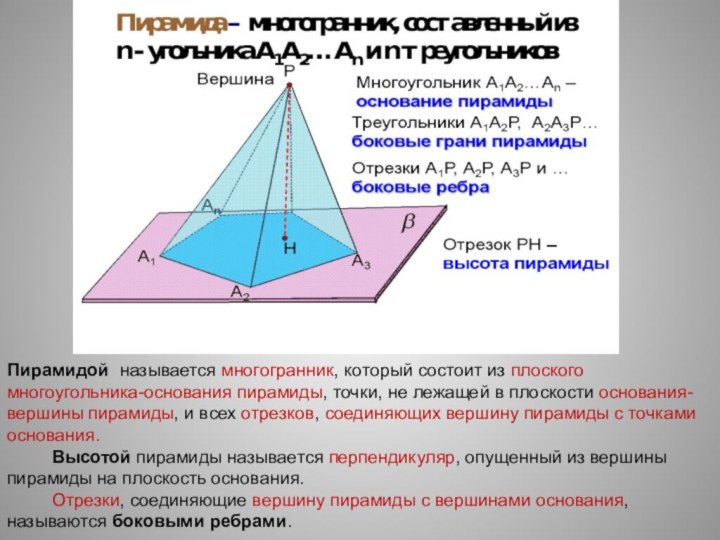
Слайд 24 Пирамидой называется многогранник, который состоит из плоского многоугольника-основания
пирамиды, точки, не лежащей в плоскости основания-вершины пирамиды, и
всех отрезков, соединяющих вершину пирамиды с точками основания.Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
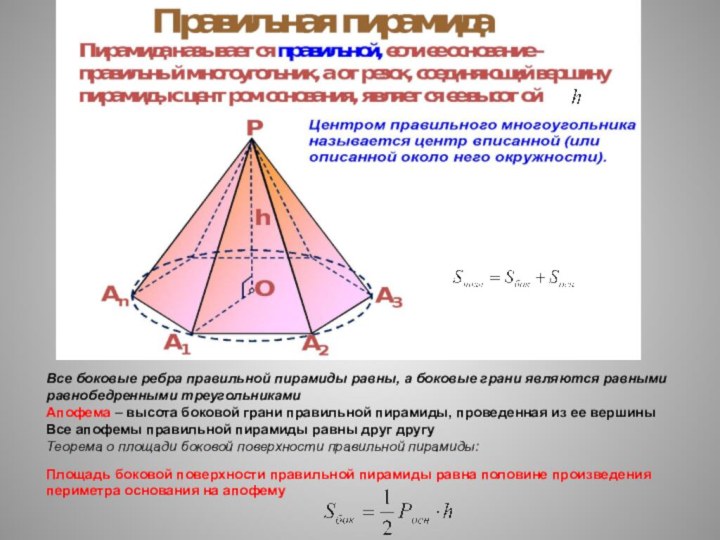
Слайд 26 Все боковые ребра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками
Апофема – высота боковой грани
правильной пирамиды, проведенная из ее вершины Все апофемы правильной пирамиды равны друг другу
Теорема о площади боковой поверхности правильной пирамиды:
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
Слайд 27
Контрольные вопросы
Продолжите предложения
1) Высотой пирамиды называется …
2)
Апофемой пирамиды называется …
3) Площадью полной поверхности пирамиды называется
…4) Площадью боковой поверхности пирамиды называется …
5) У правильной пирамиды:
а) боковые ребра …
б) боковые грани …
в) апофемы …
г) двугранные углы при основании …
д) двугранные углы при боковых ребрах …
6) Каждая точка высоты правильной пирамиды равноудалена от всех … основания
7) Боковыми гранями правильной пирамиды является …
8) Площадь боковой поверхности пирамиды равна произведению …