- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора (8 класс)
Содержание
- 2. Цель: познакомить учащихся с теоремой Пифагора и
- 3. Историческая справкаПифагор – древнегреческий ученый, живший в
- 4. 1) Историческая справка. Великий ученый Пифагор родился
- 5. С именем Пифагора связано
- 6. Система морально-этических правил, завещанная ученикам Пифагора, была
- 7. Опорное повторение по готовым чертежамКакой треугольник изображён?
- 9. Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь
- 10. Кантор (крупнейший немецкий историк математики) считает, что равенство
- 11. Прямоугольный треугольник со сторонами 3, 4
- 12. Несколько больше было известно о теореме Пифагора
- 13. Геометрия у индусов была тесно связана с
- 14. Теорема Пифагора В прямоугольном треугольнике квадрат
- 15. Вывод: с помощью теоремы Пифагора можно решать
- 16. Практическая работа Постройте в тетрадях
- 17. Стихотворение о теореме ПифагораЕсли дан нам треугольник,И
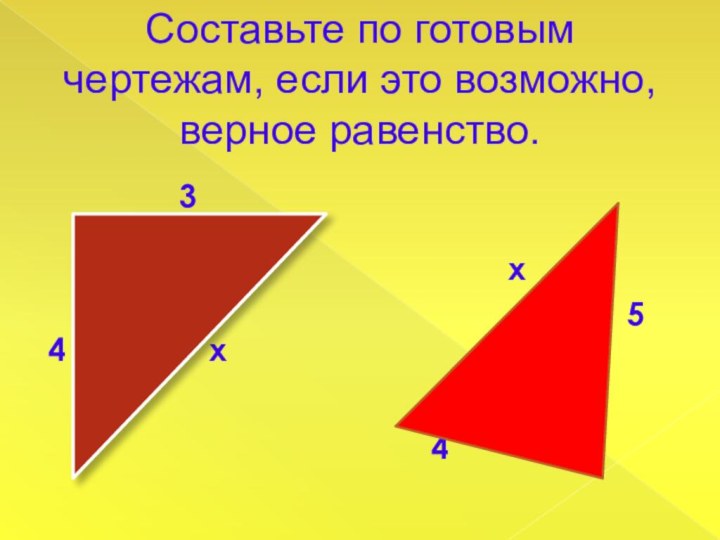
- 18. Составьте по готовым чертежам, если это возможно,
- 19. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ
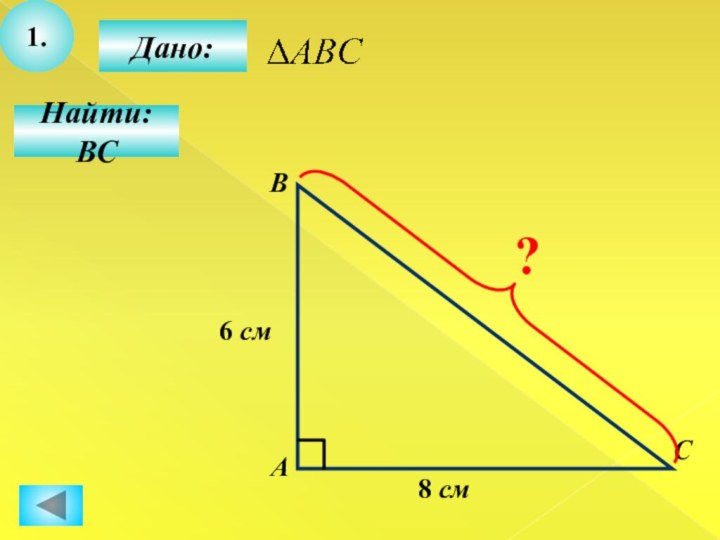
- 20. 1.Найти: ВССВАДано:8 см6 см?
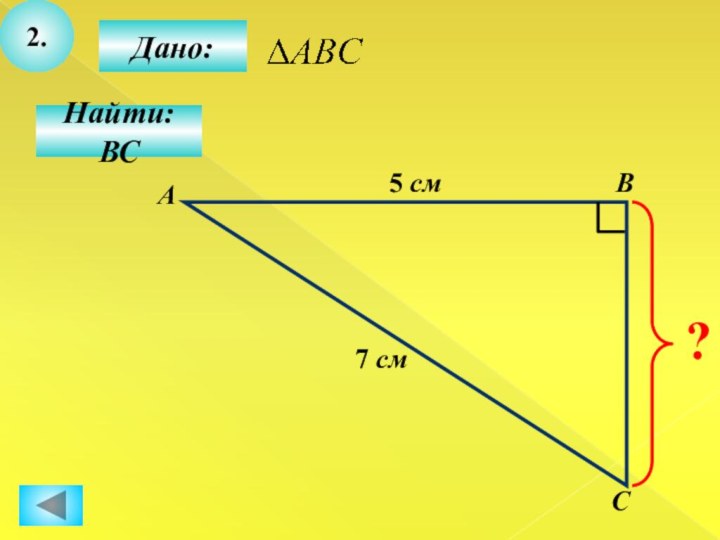
- 21. 2.Дано:СВНайти: ВСА5 см7 см?
- 22. Мобильная связьВ настоящее время на рынке мобильной
- 23. Самостоятельное решение задачи: I уровень – Коробка
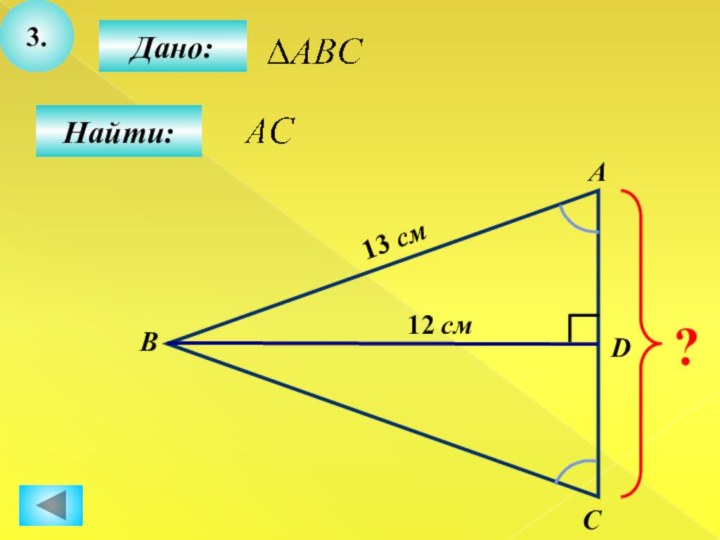
- 24. 3.Дано:Найти:АBCD?12 см13 см
- 25. Подведение итоговВозможно ли было решение задач данного
- 26. В Древнем Египте был известен треугольник
- 27. Домашнее заданиеП. 54. № 483 (б,в);
- 28. Рефлексия.Учитель: Ребята, используя рефлексивный экран, каждый
- 29. Скачать презентацию
- 30. Похожие презентации
Цель: познакомить учащихся с теоремой Пифагора и историческими сведениями, связанными с этой теоремой; развивать интерес к изучению математики, логическое мышление; внимание.






















Слайд 3
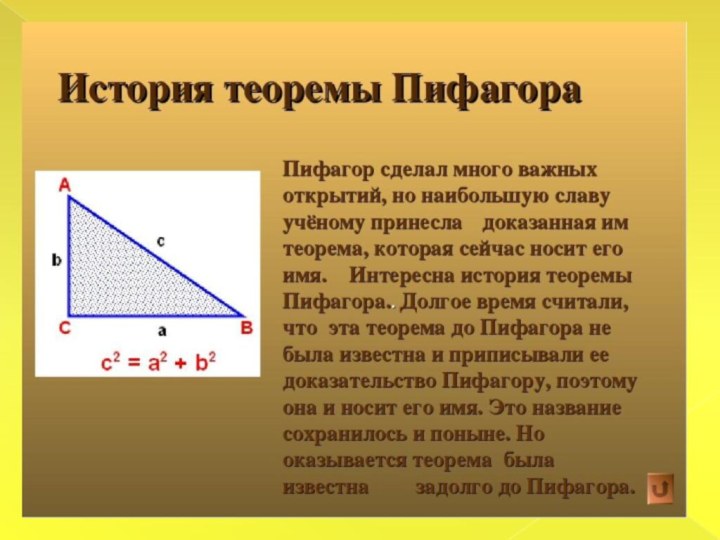
Историческая справка
Пифагор – древнегреческий ученый, живший в VI
веке до нашей эры.
Вообще надо
заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию учёного и его труды приходится реконструировать по произведениям других античных авторов, а они часто противоречат друг другу.
Слайд 4
1) Историческая справка.
Великий ученый Пифагор родился около
570 г. до н.э. на острове Самосе. Отцом Пифагора
был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам.Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".)
Слайд 5 С именем Пифагора связано много
важных научных открытий: в географии и астрономии – представление
о том, что Земля – шар и что существуют другие, похожие на неё миры; в музыке – зависимость между длиной струны арфы и звуком, который она издаёт; в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).Венчала геометрию теорема Пифагора, которой посвящён сегодняшний урок.
Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Слайд 6
Система морально-этических правил, завещанная ученикам Пифагора,
была собрана
в своеобразный моральный кодекс пифагорейцев.
Кадеты подготовили некоторые из 325
заповедей Пифагора.Не делай ничего постыдного ни в присутствии других, ни втайне.
Первым твоим законом должно быть уважение к себе самому.
Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
Никто не должен преступать меру ни в пище, ни в питии.
Будь благословенно божественное число, породившее богов и людей.
Прежде всего не теряй самоуважения!
Все исследуй, давай разуму первое место.
Делай великое, не обещая великого.
Слайд 7
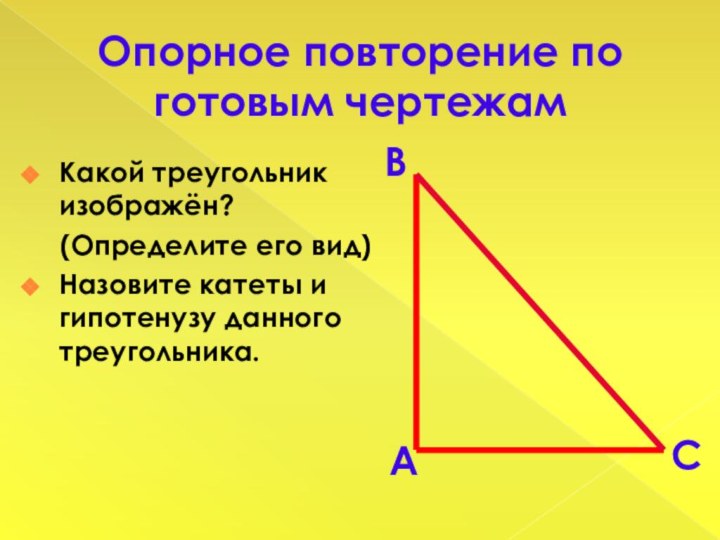
Опорное повторение по готовым чертежам
Какой треугольник изображён?
(Определите его вид)
Назовите катеты и гипотенузу данного треугольника.
В
А
С
Слайд 9 Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое
внимание привлекает математическая книга Чу-пей. В этом сочинении так
говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:Слайд 10 Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до
н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).По мнению Кантора, гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Слайд 11 Прямоугольный треугольник со сторонами 3, 4 и
5 назывался Египетским. Он получил такое название. оттого что
был известен и широко применялся еще древними египтянами. Они с помощью такого треугольника строили прямые углы на местности, что имело для них огромное значение, так как каждый год разливы Нила размывали границы между полями, и приходилось заново размечать их. Это делалось очень просто: на веревке узлами отмечалось 12 равных отрезков, а потом из этой веревки складывали треугольник, и угол, оказавшийся напротив стороны 5, являлся прямымСлайд 12 Несколько больше было известно о теореме Пифагора вавилонянам.
В одном тексте, относимом ко времени Хаммураби, т.е. к
2000 году до нашей эры, приводится приближенное вычисление гипотенузы прямоугольного треугольника; отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.Слайд 13 Геометрия у индусов была тесно связана с культом.
Весьма вероятно, что теорема о квадрате гипотенузы была известна
в Индии уже около 8 века до нашей эры. Наряду с чисто ритуальными предписаниями, существуют и сочинения геометрически теологического характера, называемые Сульвасутры. В этих сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.Пифагор, по-видимому, нашел доказательство этого соотношения. Отсюда и название этой теоремы.
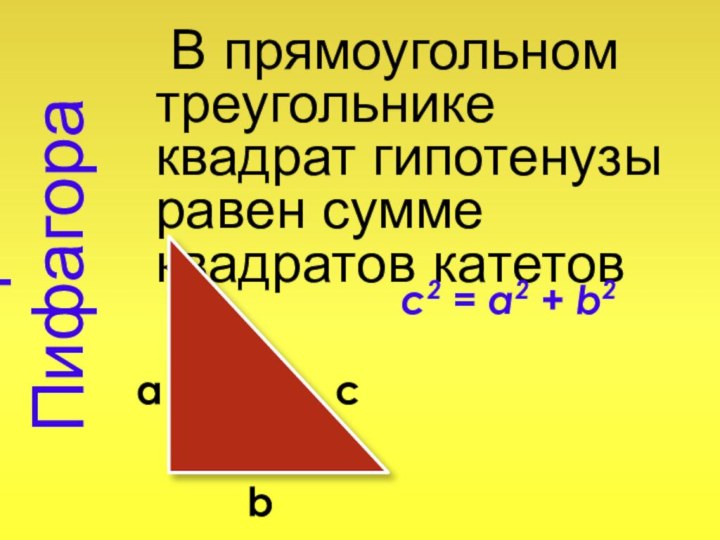
Слайд 14
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов
c2 = a2 + b2a c
b
Слайд 15 Вывод: с помощью теоремы Пифагора можно решать два
вида задач:
1. Найти гипотенузу прямоугольного треугольника, если известны
катеты.2. Найти катет, если известна гипотенуза и другой катет.
.
Слайд 16
Практическая работа
Постройте в тетрадях прямоугольный треугольник (с
катетами, длина которых для удобства выражается целыми числами).
Измерьте катеты
и гипотенузу. Результаты измерений запишите в тетрадях.Возведите все результаты в квадрат, т. е. Узнайте величины a2; b2; c2.
Сложите квадраты катетов (a2 + b2) и сравните с квадратом гипотенузы.
У всех ли получилось, что a2 + b2 = с2?
Слайд 17
Стихотворение о теореме Пифагора
Если дан нам треугольник,
И притом
с прямым углом.
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,Сумму степеней находим –
И таким простым путём
К результату мы придём.
(И. Дырченко)
Слайд 22
Мобильная связь
В настоящее время на рынке мобильной связи
идет большая конкуренция среди операторов. Чем надежнее связь, чем
больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим ответ.
Ответ: 2,3 км.
Слайд 23
Самостоятельное решение задачи:
I уровень – Коробка конфет
имеет форму равнобедренного треугольника, боковая сторона которой равна 25см,
а основание – 14см. Какова высота этой коробки? (Ответ: 24см)II уровень – Цветочная клумба имеет форму равнобедренной трапеции с основаниями10 и 18 см, и с боковой стороной равной 5см. Найти площадь клумбы. (Ответ: 42см2)
Слайд 25
Подведение итогов
Возможно ли было решение задач данного типа
без применения теоремы Пифагора?
В чём суть теоремы Пифагора?
Для любых
ли треугольников можно применить данную теорему?Слайд 26 В Древнем Египте был известен треугольник со
сторонами 3, 4, 5; его использовали при разметке прямоугольных
земельных участков после ежегодного уничтожения их границ разлившимся Нилом. Для построения прямых углов египтяне поступали так: на веревке делали метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым.Занимаясь поисками треугольников, стороны которых a, b, c удовлетворяли бы условию a2 + b2 = c2, Пифагор нашел формулы, которые в современной символике могут быть записаны так:
a = 2n + 1, b = 2n(n + 1), c = 2n2 + 2n + 1, n Є Z.
Треугольник с такими сторонами является прямоугольным:
n = 1: а = 3, b = 4, с = 5 (приведите примеры самостоятельно).
Где применяется, по вашему, сейчас теорема Пифагора?
Слайд 28
Рефлексия.
Учитель: Ребята, используя рефлексивный экран, каждый из
вас, выскажите, пожалуйста, своё мнение о нашем занятии, дополнив
понравившиеся вам фразы своими мыслями.(У детей на столах отпечатаны карточки с изображениями формулы теоремы Пифагора, рисунками её применения, с фразами, они заполняют их и прикрепляют на доске под портретом Пифагора).
сегодня я узнал…
теперь я могу…
я научился…
раньше я не знал, что…
меня удивило…
было интересно…
было трудно…
я понял, что…
Учитель: Спасибо за урок!