- Первый признак
-
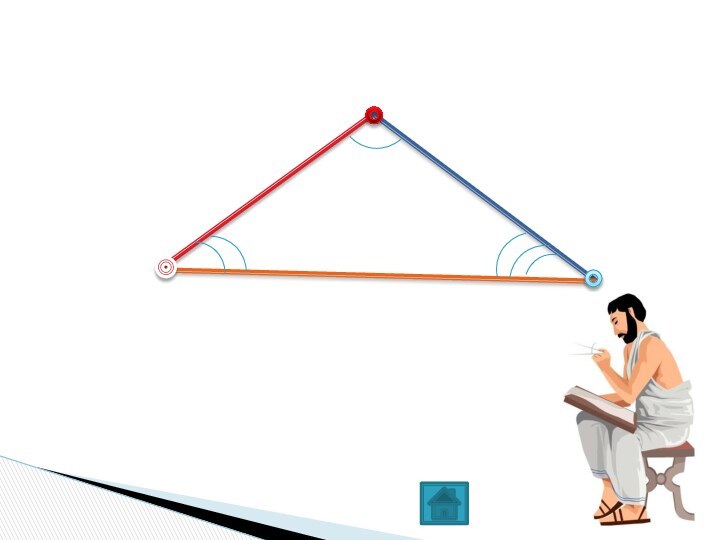
Второй признак- Третий признак
Задача Наполеона
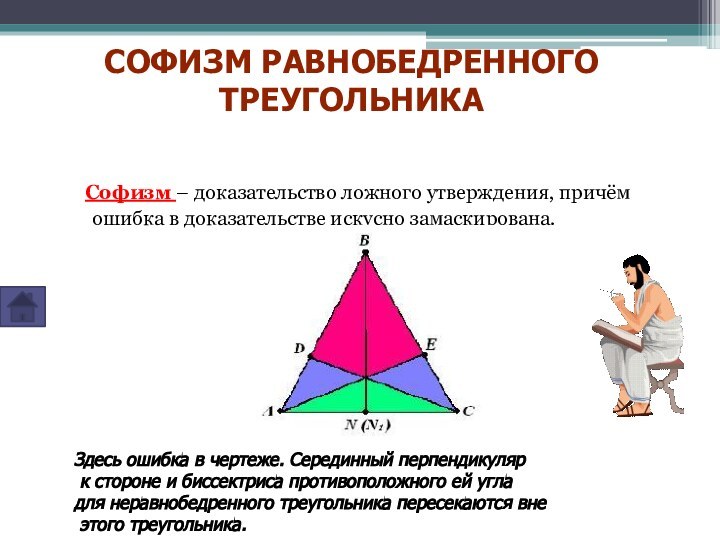
Софизм равнобедренного треугольника
Треугольник Паскаля
Теорема синусов и косинусов
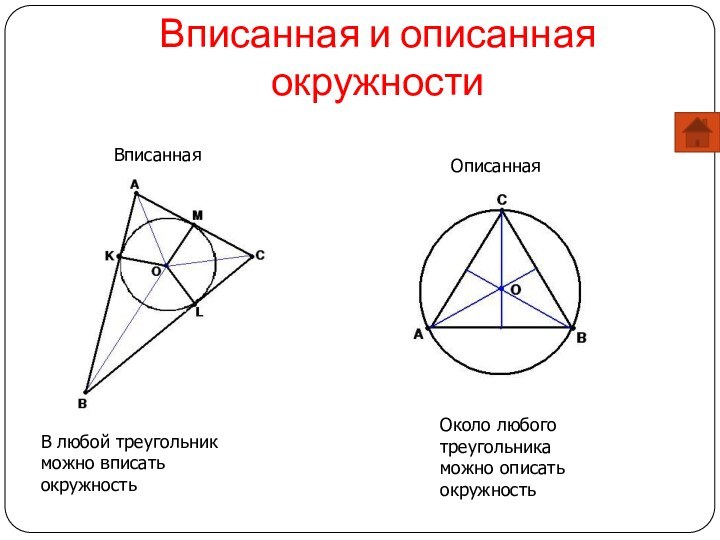
Вписанная и описанная окружности
Содержание
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










Содержание
Признаки равенства треугольников
А
В
С
А
В
С
1
1
1
Признаки равенства треугольников
А
В
С
А
В
С
1
1
1
Признаки равенства треугольников
А
В
С
А
В
С
1
1
1
Синусы
Косинусы
Софизм равнобедренного
треугольника