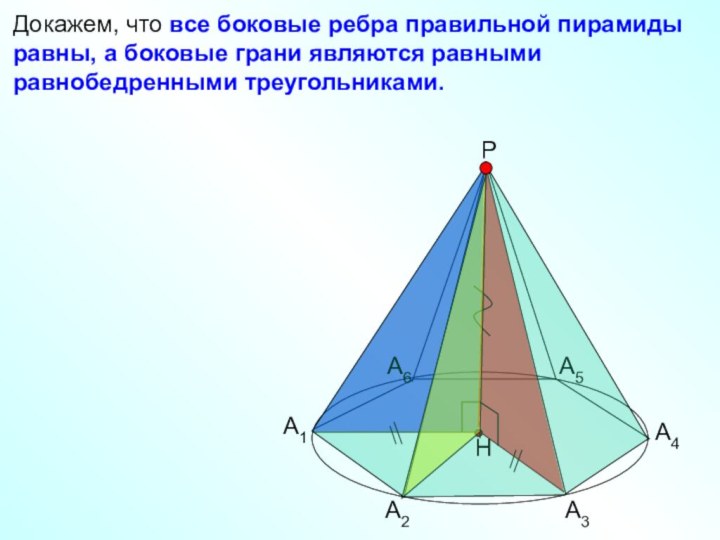
пирамидой.
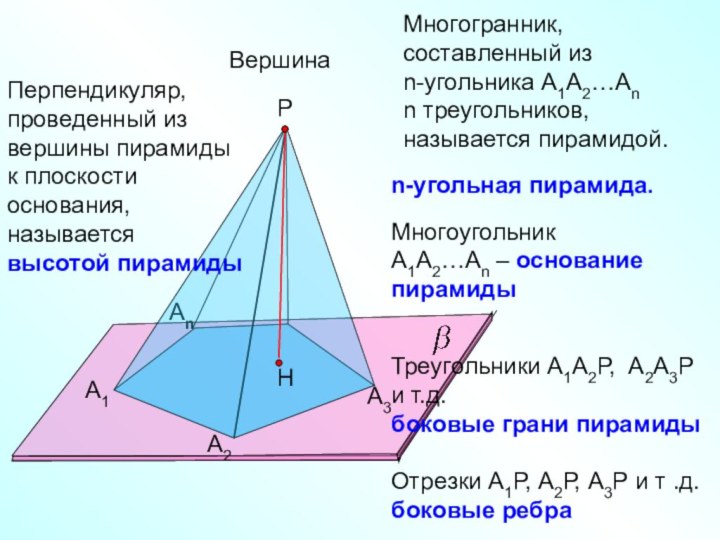
Вершина
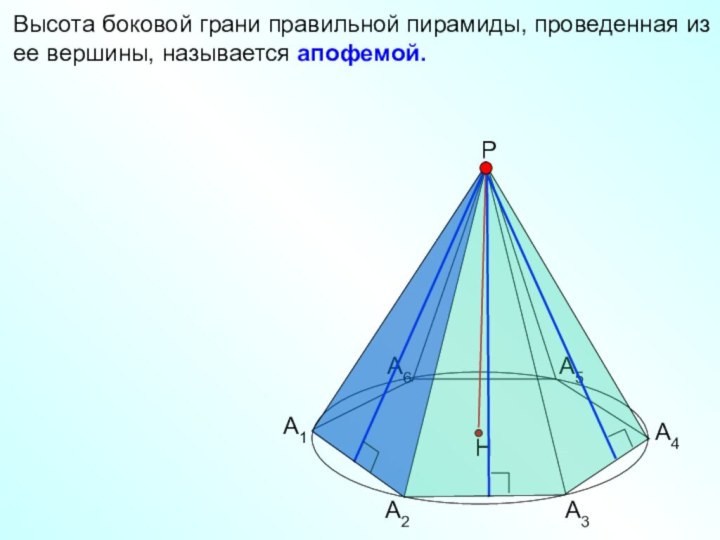
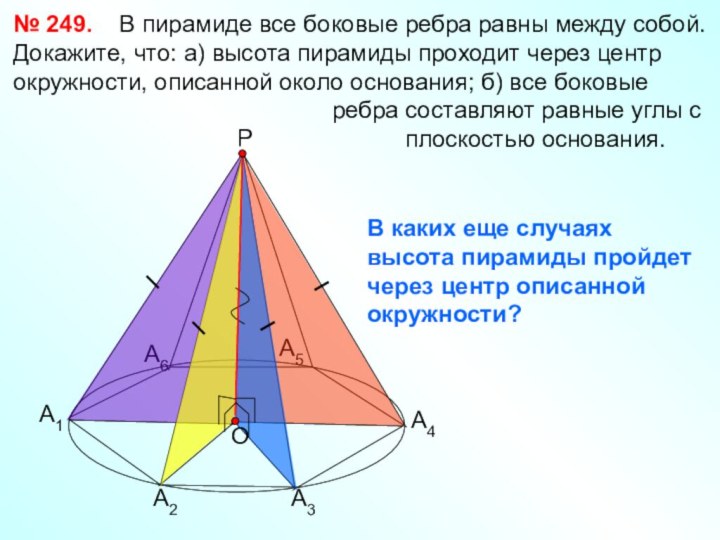
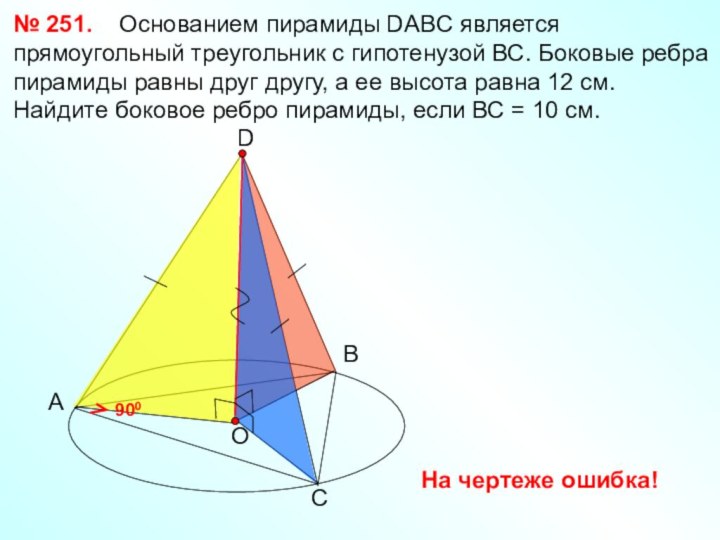
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется
высотой пирамиды
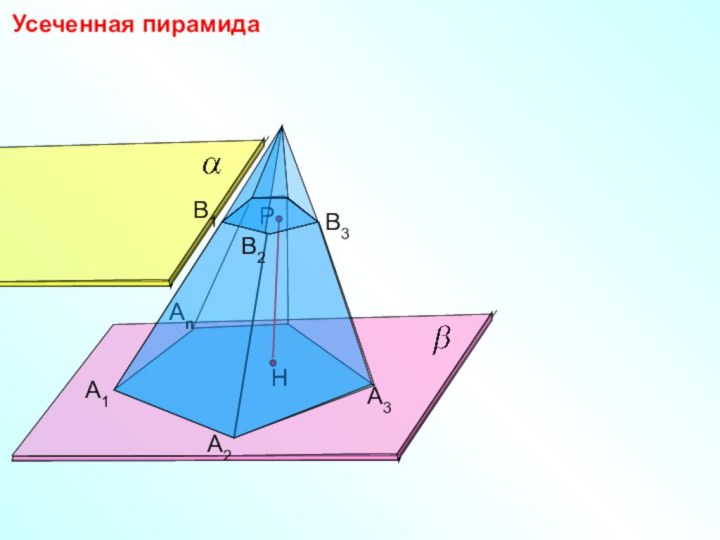
n-угольная пирамида.
Многоугольник
А1А2…Аn – основание пирамиды
Треугольники А1А2Р, А2А3Р и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и т .д.
боковые ребра